Let's break down Timsort – the fast, hybrid sorting algorithm that efficiently sorts data big and small without breaking a sweat!
When it comes to sorting algorithms, none of them are perfect. Take a look at the following table of running times for the sorting algorithms we've seen so far:
| Name | Average Time | Best Time | Worst Time |
|---|---|---|---|
| Quicksort | O(n log n) | O(n log n) | O(n²) |
| Mergesort | O(n log n) | O(n log n) | O(n log n) |
| Bubble Sort | O(n²) | O(n) | O(n²) |
| Selection Sort | O(n²) | O(n²) | O(n²) |
| Insertion Sort | O(n²) | O(n) | O(n²) |
| Counting Sort | O(n + k) | O(n + k) | O(n + k) |
| Radix Sort | O(d·(n + k)) | O(d·(n + k)) | O(d·(n + k)) |
These sortings algorithms that seem perfect often show really poor behavior in worst-case scenarios. Their best-case performance may be suboptimal as well.
Take quicksort for example. Quicksort looks pretty good, right? On average it runs at a very respectable O(n log n) time. Now, what if we ask it to sort a fully sorted collection of values, and our pivot selection is having an off day? In this case, quicksort will slow to a crawl and sort our input with a O(n²) time. That makes it as bad as some of our slowest sorting algorithms.
The opposite holds true as well. Our slowest sorting algorithms, like Selection Sort, Insertion Sort, or Bubble Sort have the potential to run really fast. For example, Bubble Sort normally runs at O(n²). If the values we ask it to sort happen to already be sorted, Bubble Sort will sort the values at a blazing fast O(n) time. That's even faster than Quicksort's best sorting time:

How well our sorting algorithms work depends largely on the arrangement of our unsorted input values:
Based on our answers to these questions, the performance of our sorting algorithms will vary. As we described a few seconds ago, seemingly great sorting algorithms will crumble with the wrong arrangement of values, and terrible sorting algorithms will shine on the same arrangement of values. So...what can we do here?
Instead of using a single sorting algorithm for our data, we can choose from a variety of sorting algorithms optimized for the kind of data we are dealing with. We can use something known as a hybrid sorting algorithm. A hybrid sorting algorithm takes advantage of the strengths of multiple sorting algorithms to create some sort of a super algorithm:

By relying on multiple sorting algorithms, we can minimize the worst-case behavior of individual sorting algorithms by switching between algorithms based on the characteristics of the unsorted input data being sorted.
In this article, we are going to learn about one of the greatest hybrid sorting algorithms ever created. We are going to learn about Timsort.
Onwards!
Timsort is a hybrid sorting algorithm that combines the best features of two other sorting algorithms: Merge sort and Insertion sort. The key idea behind Timsort is to take advantage of the existing order in the data. It's especially efficient for real-world scenarios where the values we'll be sorting will often have some pre-existing order or patterns.
The way Timsort works can be grossly oversimplified as follows:
The best way to make sense of how Timsort works is by walking through an example, so we'll do that next.
As with all great sorting algorithm walkthroughs, we are going to start with some unsorted data that needs to be sorted:

This list of unsorted values is pretty long to help us better appreciate how Timsort works. To help make all of this data easier for us to visualize here, let’s to wrap this long list of data as follows:

Nothing about our data has changed except how we can represent it on this page. The first thing we do with Timsort is divide the data we wish to sort into smaller chunks. These chunks are more formally known as runs. The size of these runs usually varies between 32 and 64 items, but for our example, we’ll keep the size of our runs much smaller at 4:

Notice that we divided our entire unsorted collection into runs of four items each, except for the last run, which only has two values.
Now that we have our runs, we perform insertion sort on each run to sort these values. We sort our first run:

Next, we sort our second run:

This sorting repeats until all of our individual runs are sorted:

An important detail to note is that only the values inside each run are sorted. In aggregate, our collection of items is still unsorted. We will address that next.
The final step is for us to take our individually sorted runs and merge them into larger and larger sorted runs. At the end of all this, the final result will be one combined sorted collection of data.
We start by merging adjacent runs together, and I have color-coded the adjacent runs that will be merged first:

The merging operation will use a subset of merge sort’s capabilities where we need to merge the individually sorted runs into a final sorted order. After the first round of merging, our collection will look as follows:

Our runs are now around double in size. We now repeat the process by merging adjacent runs again. After this round of merging, we will be left with two sorted runs:

We are almost done here. All that remains is one last step, where we merge our two unsorted runs to create our sorted output:

At this moment, no further runs need to be merged. Timsort is finished with sorting our data. Also, at this very moment, you probably have many questions about what exactly happened to make Timsort seem like a superior sorting algorithm to most other sorting algorithms out there. We'll address that next.
The above walkthrough highlighted how we can use Timsort to sort our unsorted collection of numbers. We broke our larger input down into runs, sorted each of those runs using insertion sort, and wrapped things up by merging adjacent runs until we ended up with a single fully sorted run. If we analyzed our walkthrough at face value, Timsort’s performance may not seem very fast where we have n items, n2 running time for insertion sort, and a logarithmic running time for merging values. This is where some of the optimizations that Timsort is known for kick in to speed things up...dramatically in many cases. These optimizations revolve around detecting common patterns in our data and customizing the next steps to account for how the data is structured.
The worst-case running performance for insertion sort happens when the values it is sorting are fully in reverse. To avoid this, Timsort will try to identify runs that are strictly in reverse (aka descending) order and do an in-place reverse on them first before attempting to sort and merge them:

The best case performance for insertion sort occurs when we are dealing with runs whose values are in ascending order. In these cases, the runs are left as-is. There is no need to sort them. The only real work Timsort will need to perform is the merging operation, which is a consistently fast operation.
Galloping mode (also known as binary search insertion by distant friends and relatives) is an optimization technique used in Timsort algorithm during the merging phase. It's designed to handle cases where a run has many elements that are already in their final sorted position relative to the other run.
Here's how it works:
This will make more sense with an example, so here are two sorted runs we would like to merge:

In an unoptimized merge, we would compare each element between both runs and add the smaller of the values to our merged collection. When we look at the values in Run A, we can see that the first five numbers are all consistently less than the first value in Run B. If we elaborate on that using a loose array-like syntax, we have:
At this point, our merged collection looks as follows:

Now, Timsort will compare RunA[5] (31) with RunB[0] (10):

At this point, 10 is smaller than 31, so Timsort will now check the next few elements from Run B to see if they should be added in bulk:
Since all elements in Run B are smaller than RunA[5], Timsort adds them all at once to the merged collection:

After adding all the elements from Run B, Timsort reverts to the regular comparison mode and continues merging the remaining items. In this case, both 31 and 48 from Run A will be added to the end of the merged collection.
By using galloping mode, Timsort is able to speed up the merging process by quickly adding multiple consecutive elements from one run when it's clear that they are all smaller (or larger) than the next element in the other run. This reduces the number of comparisons and overall sorting time, especially when merging runs of significantly different sizes.
Timsort’s merging strategy is adaptive, meaning it can vary the merging order based on the sizes of the runs. The goal is to maintain balance among the runs and avoid having a single, large run at the end that would make the final merge costly.
For example, let’s say these are the runs we are dealing with:

The actual values of the runs aren’t important. What is important is the size of the runs. To avoid any run from being too large and making the merge waaaaay unbalanced, we start by merging the two smallest runs:

This would result in Runs C and D merging to create Run CD:

This process continues to ensure the smallest runs are merged as part of creating a final merge pair whose sizes are similar.
Yes, insertion sort is a slow sorting algorithm. When sorting a small number of values, though, this slowness isn’t very noticeable. This is especially true in a world where our computers can process millions and billions (and trillions?) of operations a second.
For this reason, Timsort will often fall back to using plain old insertion sort when the size of the input it is trying to sort is less than the run size threshold - which is usually 32 or 64 items in length:
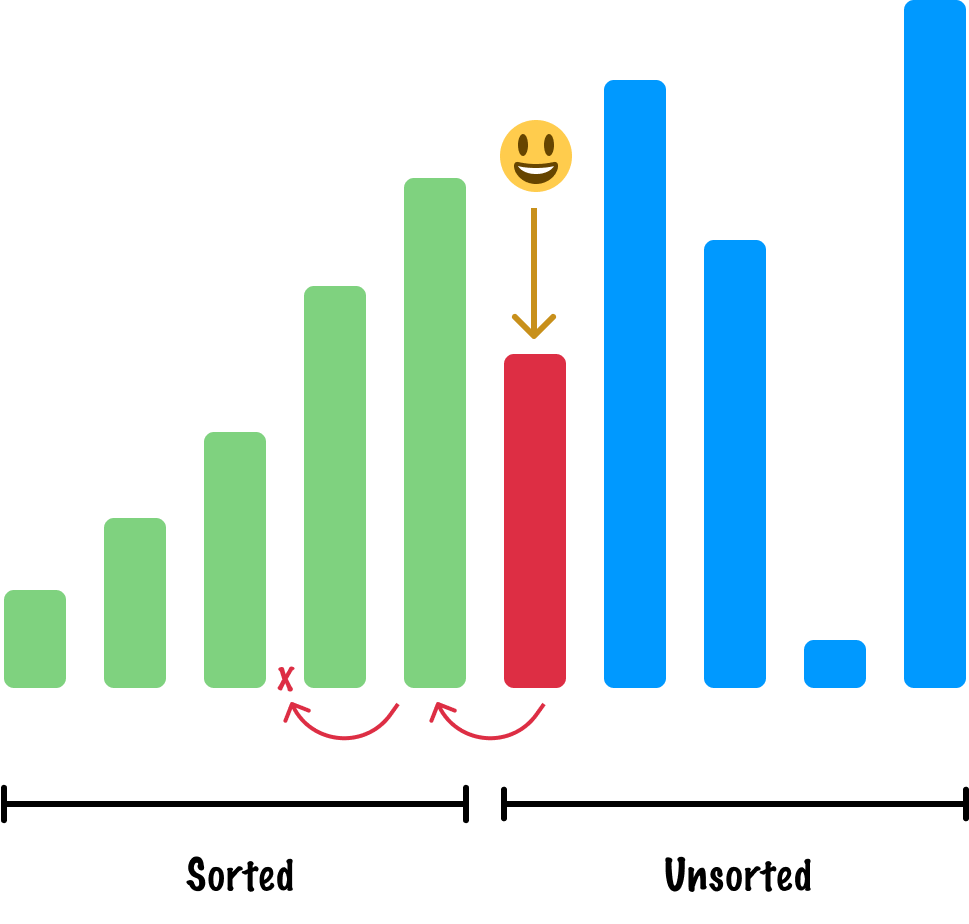
This avoids the added overhead of the merging operation, breaking runs, and so on.
Why is Timsort so efficient? It is because it tries to detect patterns in the sorted data and special case the sorting behavior accordingly. Whether it is by identifying natural runs, detecting reversed runs, using galloping mode to avoid unnecessary merging-related work, enforcing minimum run lengths, or performing adaptive merges, Timsort tries to take the most efficient path whenever possible. A subtle but important detail is that these pattern matching optimizations ensure that Timsort performs well on partially sorted data which is the most common type of data we will encounter in the real world.
Timsort is one of the best sorting algorithms out there, and we can see it live up to its grandness when we summarize its time and memory complexity below:
| Scenario | Time Complexity | Memory Complexity |
|---|---|---|
| Best case | O(n) | O(n) |
| Worst case | O(n log n) | O(n) |
| Average case | O(n log n) | O(n) |
At its best, Timsort can run in linear time. This happens when the data is already sorted or nearly sorted as part of a few large runs, and we know that Insertion Sort runs in linear time for sorted data:

Merging runs is a fast operation as well, and if we throw in any optimizations such as galloping mode if the range of sorted numbers don't overlap, the merging is almost a trivial operation.
In the average and worst cases, Timsort runs at O(n log n). The bulk of the complexity here goes into identifying runs and merging them. This puts its performance on par with Quicksort's average performance, but Timsort's optimizations give it an edge as being a faster O(n log n)! This is validated by benchmarks such as the following that compares Timsort with Quicksort on partially sorted data:

Notice how much faster Timsort is when we compare it to Quicksort. The more Timsort is used in real-world data scenarios, the more we'll see it soaring faster than every other sorting algorithm we have seen so far.
Lastly, from a space point of view, Timsort needs an O(n) amount of memory to run. This has to do with the various data structures Timsort creates behind the scenes as part of merging the various runs.
Timsort is a very complex sorting algorithm to implement. The core insertion sort and merging capabilities are straightforward. Identifying and handling all the various patterns to optimize for...is less straightforward. For that reason, most examples of Timsort we will run into is based on the original Python implementation itself. I am not going to paste the massive amount of code needed to implement Timsort in JavaScript.
Instead, here is a link to the Github repo where I took Marco Ziccardi's Node.js implementation of Timsort and turned into something that works in the browser:

As we scan through the code, we'll see a lot of familiar patterns. Towards the bottom, the example code to initialize Timsort and use it to sort some values is provided:
let example = [-7, 10, 50, 3, 940, 1, 4, -8, 24, 40, 33, 12, 10];
// Comparison function
function numberCompare(a, b) {
return a - b;
}
// Sort our example array
timsort.sort(example, numberCompare);
console.log(example);Feel free to try it out and use this in your own projects, but as we will discuss in a few moments, Timsort is already the default sorting algorithm used in many situations in our favorite programming languages.
Timsort, as the pre-eminent hybrid sorting algorithm, is one of the fastest sorting algorithms we have. When we say this, this fastest isn't qualified with caveats where the unsorted input needs to be of a certain arrangement. Timsort's worst-case behavior is very good. Timsort's best-case behavior is very VERY good. The upper and lower bounds of its performance make it a great choice for any kind of unsorted (or sorted) input we throw at it. This flexibility and power is what makes Timsort one of the default sorting algorithms across various programming languages like Python, Java, Rust, and more.
Now, Timsort isn't the only hybrid sorting algorithm in town. Another popular hybrid sorting algorithm is introsort (sometimes referredt to as introspective sort) that uses a combination of quicksort, heapsort, and insertion sort for its sorting shenanigans. Introsort is the default sorting algorithm in Swift, C#, and other languages. As we look ahead into the future and run into more interesting and new data scenarios, we may see more hybrid sorting algorithms emerge. We are in the early days here, so there will be more fun times to be had with hybrid sorting algorithms in the future.
Just a final word before we wrap up. What you've seen here is freshly baked content without added preservatives, artificial intelligence, ads, and algorithm-driven doodads. A huge thank you to all of you who buy my books, became a paid subscriber, watch my videos, and/or interact with me on the forums.
Your support keeps this site going! 😇

:: Copyright KIRUPA 2025 //--