Table of Contents
When we look around, a lot of the data around us is hierarchical, with a clear relationship between a parent and child. Common examples include family trees, organizational charts, flow charts/diagrams, and more. Below is a famous example popularized by xkcd:
While we can certainly represent hierarchical data using linear data structures like arrays or linked lists, just like it is certainly possible to eat soup using a plate and fork, it isn’t optimal. There are better ways. One of the better ways is the tree data structure.
In the following sections, we’ll learn a whole lot about trees and set ourselves up nicely to go deeper into popular tree-related topics in the future.
Onwards!
To retrace our steps a bit, a tree data structure is a way of organizing data in a hierarchical manner. Just like in nature, trees in our computer world come in many shapes and sizes. For our purposes, let’s visualize one that looks as follows:
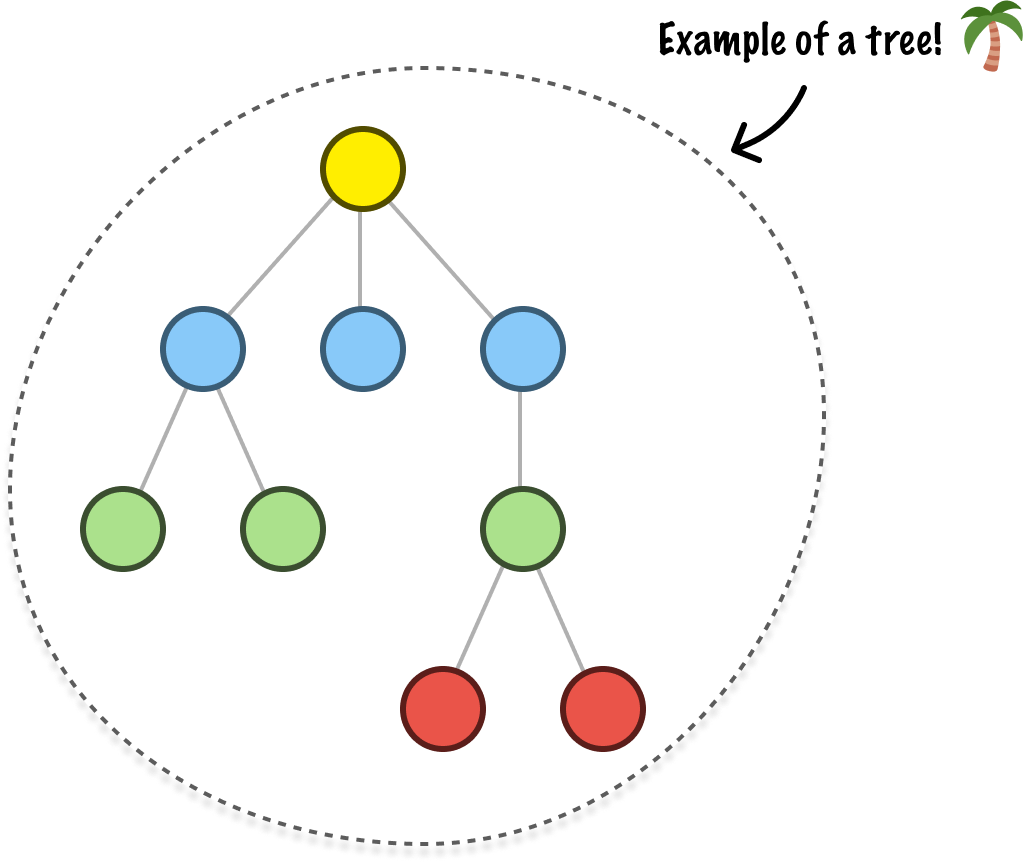
We see a bunch of circles and lines connecting each circle. Each circle in the tree is known as a node. The node plays an important role in a tree. It is responsible for storing data, and it is also responsible for linking to other nodes. The link (visualized as a line) between each node is known as an edge:
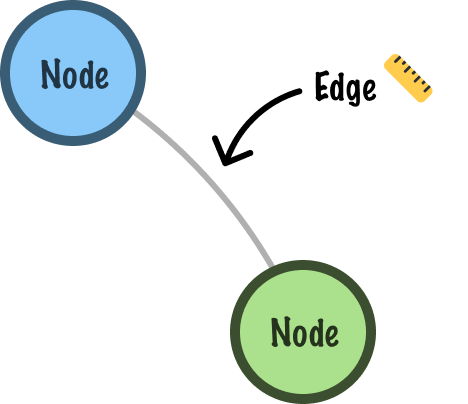
Now, just saying that our tree has a bunch of nodes connected by edges isn’t very enlightening. To help bring some more clarity, we give them additional labels such as children, parents, siblings, root, and leaves.
The easiest nodes to classify are the children. There are many of them, for a child node is any node that is a direct extension of another node. Except for the very first node at the very top, all of the nodes we see here fit that description and would be considered to be children:
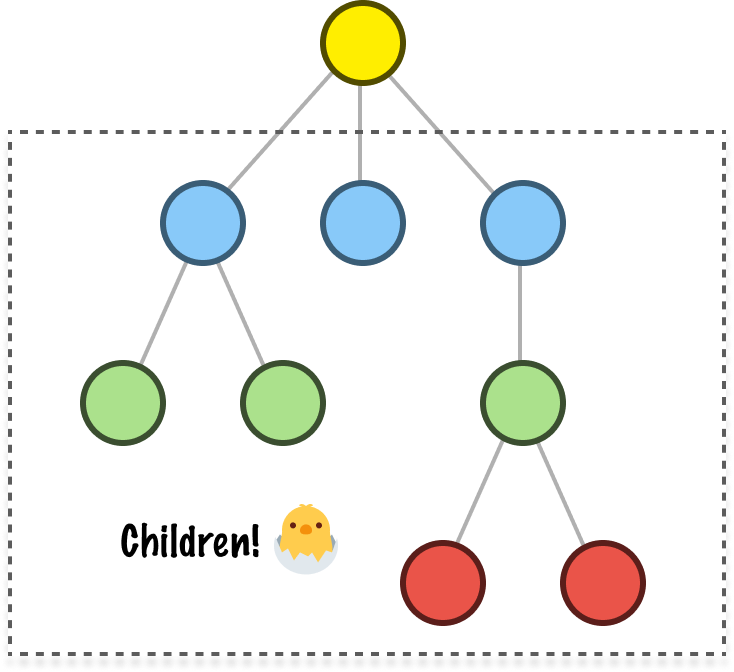
When we have child nodes, we also have parent nodes. A parent node is any node that has children:
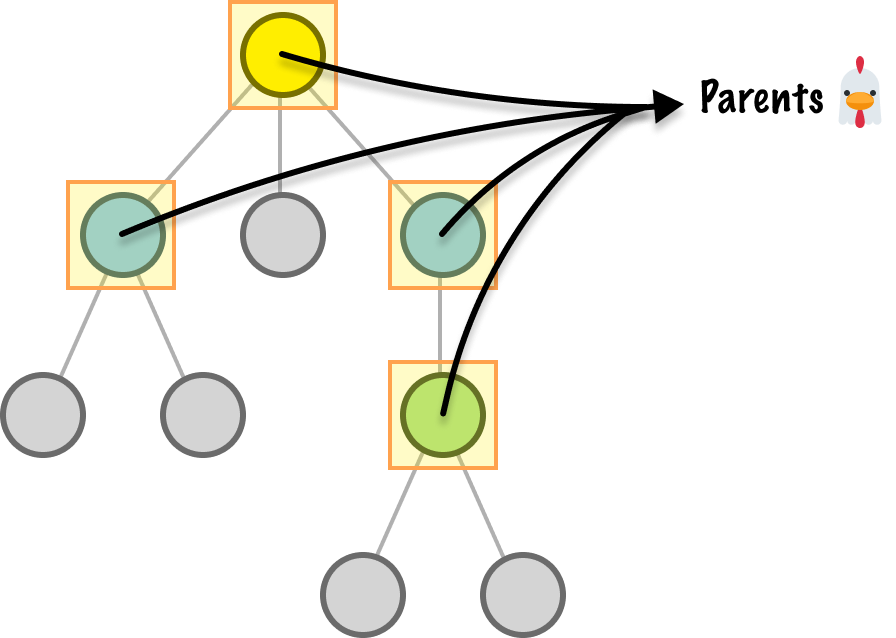
One thing to call out is that the meaning of parent or children is relative depending on what part of the tree we are looking at. A node can be a child, a parent, a grandparent, a grandchild, and more all at the same time:
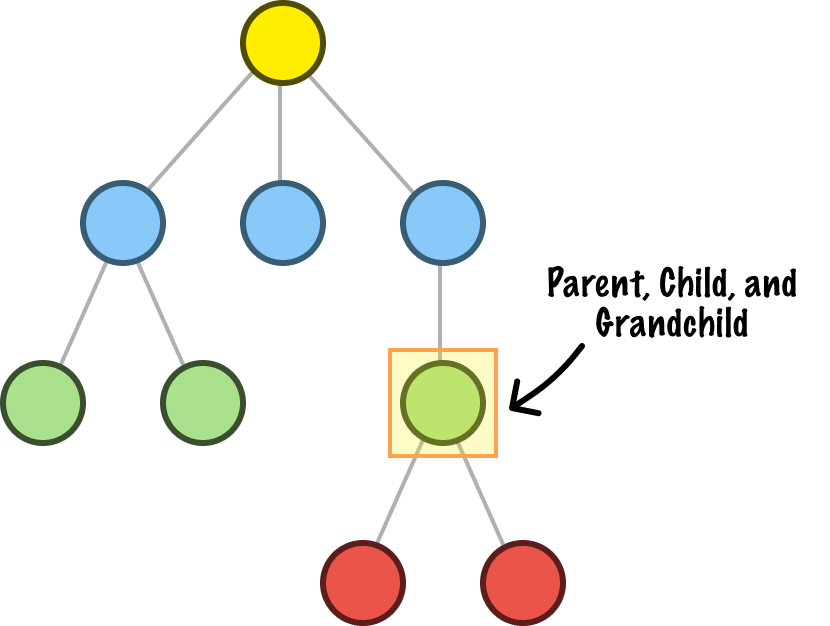
It is convention to never go beyond referring to a node as just a child or just a parent, though. Adding extra familial layers adds more complexity, especially since we have different ways of specifying the exact layer in the hierarchy a node is present in.
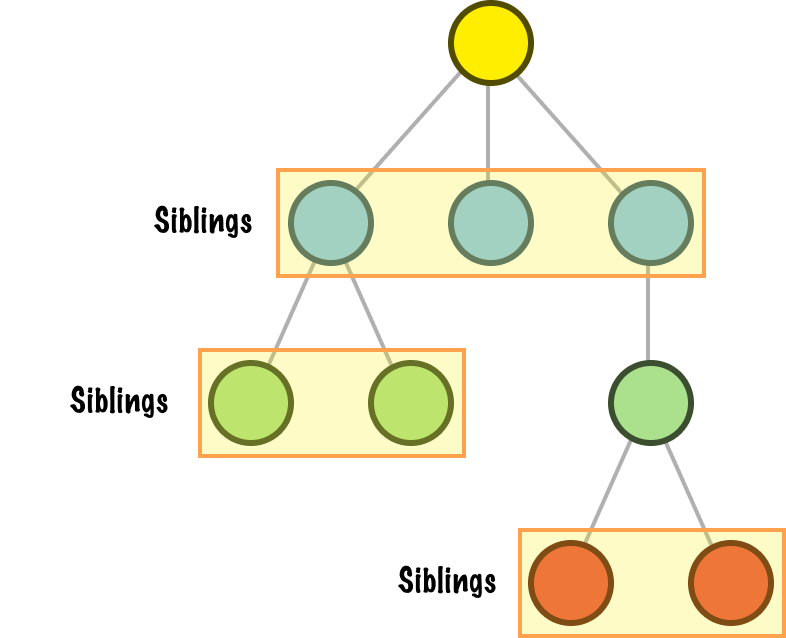
With that said, there is one more family relationship that we will encounter frequently. That one is siblings, which are all the children of the same parent:
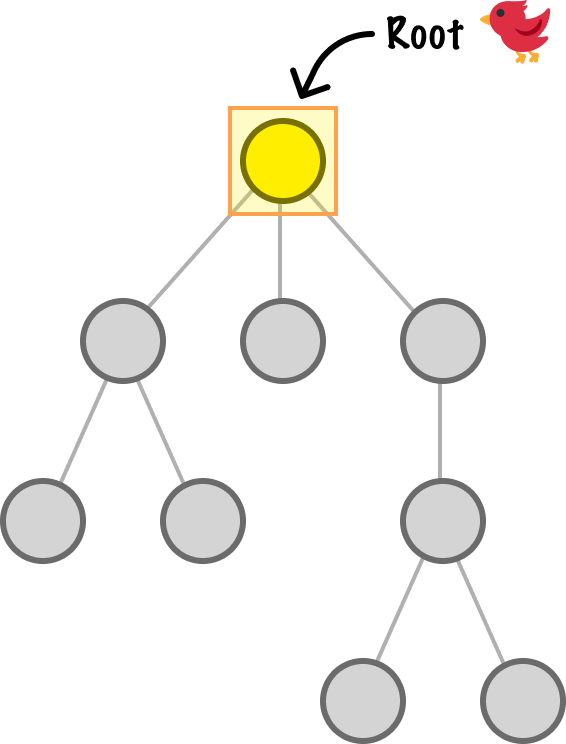
We are almost done here. Earlier, we said that all nodes are children except for the first node at the very top, which has no parent. This node is better known to friends, family, and computer scientists as the root:
While the root is a node that has no parent, on the other end are the nodes that don’t have any children. These nodes are commonly known as leaves:
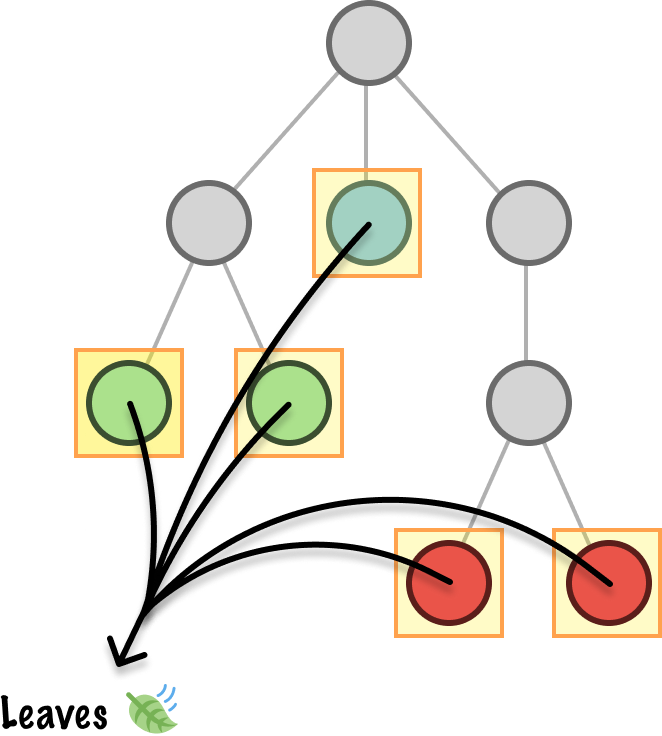
All righty. At this point, we covered the basic properties of trees and the many names we can give to each node depending on how zoomed in or zoomed out we are when looking at them. There are a few more tree properties and node groupings that have special names, but we'll cross those when we get to them later.
When we look at each node in our tree, the height and depth are little details used to describe the relative position of nodes within the tree. If we had to define both:
These definitions aren't the easiest ones to fully wrap our brains around. The easiest way to make sense of all this is by taking our example tree and seeing what the height and depth for each node will be. Take a close look at the following:
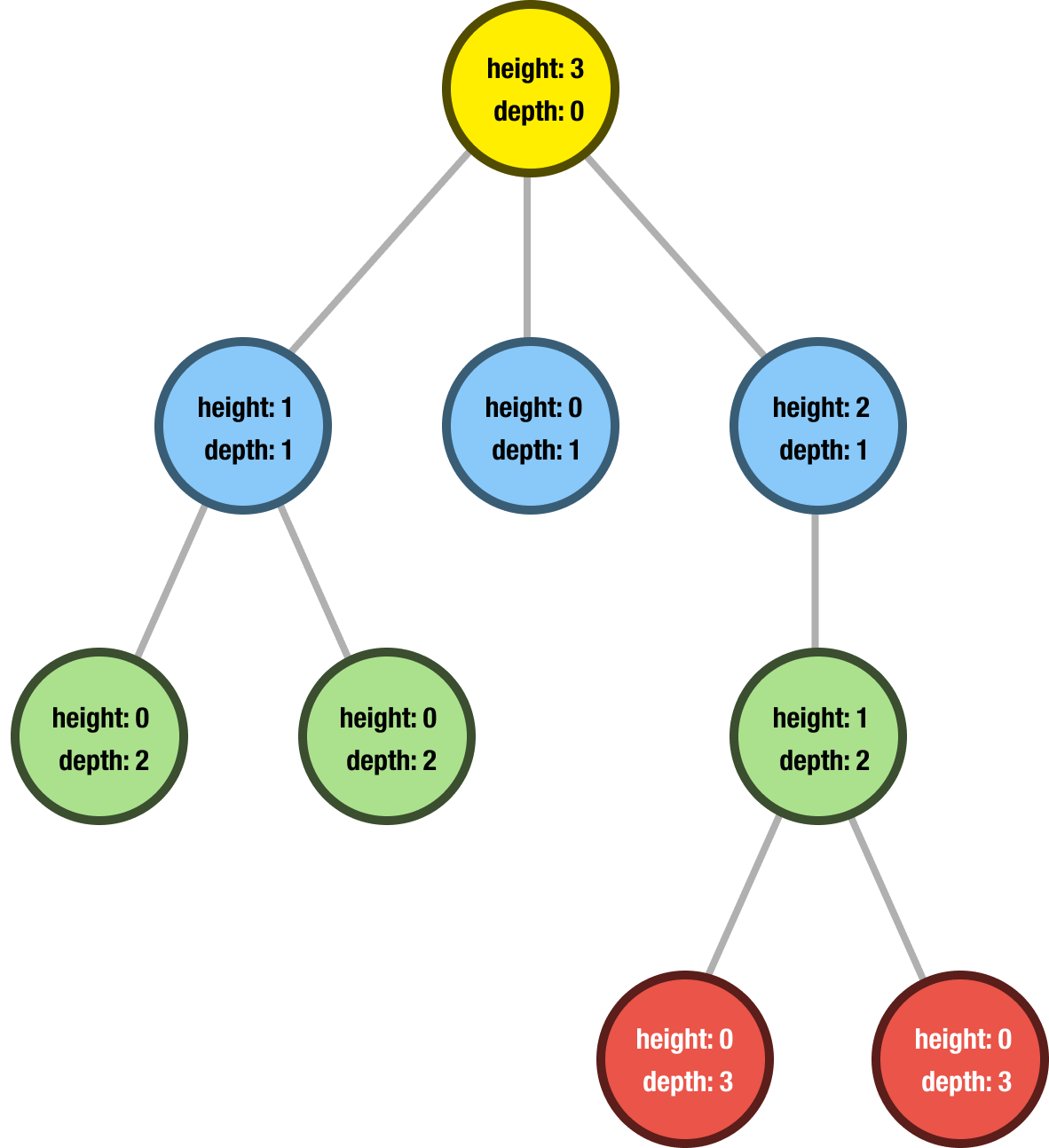
Some things to note is that the value for height is relative to each node, depending entirely on far away the furthest leaf node is. The value for depth is global to the tree, and it doesn't matter what the shape of our tree is. The root of the tree has a depth of 0, the next layer of children has a depth of 1, and so on.
Alright, my leaf-loving friends, we've finally come to the end of our little deep dive through the zany world of the tree data structure. While thinking through how our data will fit into this tree-like format may seem a little daunting at first, we will go further in subsequent articles to ensure we all become tree hugging experts! So the next time you're feeling a little stumped, just remember to tree-t yourself to a nice cup of coffee, put on your thinking cap, and branch out...ok, I'll stop.
Just a final word before we wrap up. If you have a question and/or want to be part of a friendly, collaborative community of over 220k other developers like yourself, post on the forums for a quick response!
