One of the most popular sorting algorithms you'll bump into is mergesort. It was designed in the 1940's when dinosaurs roamed the jungles:

Ever since then, mergesort (and variants of it!) can be seen everywhere - ranging from sort implementations in the Perl, Python, and Java languages to sorting data in tape drives. Ok, maybe the tape drives bit isn't relevant today, but mergesort comes up in a lot of places due to its efficiency.

In this article, we are going to take a detailed look at how mergesort does its thing and wrap it up with a simple JavaScript implementation that brings it to life.

Onwards!

How Mergesort Works

Trying to understand how mergesort works will seem overwhelming at first, but let's take it easy by walking through an example. In our example, we have nine numbers that we'd like to sort:

 

 

One quick aside. I should mention that mergesort is a divide and conquer algorithm...and it is quite shameless about that. All that it means is that mergesort performs its magic on numbers by dividing them into smaller and smaller sections first. Right now, we have nine numbers that we threw at mergesort. The first thing mergesort does is break that up into two halves:

 

 

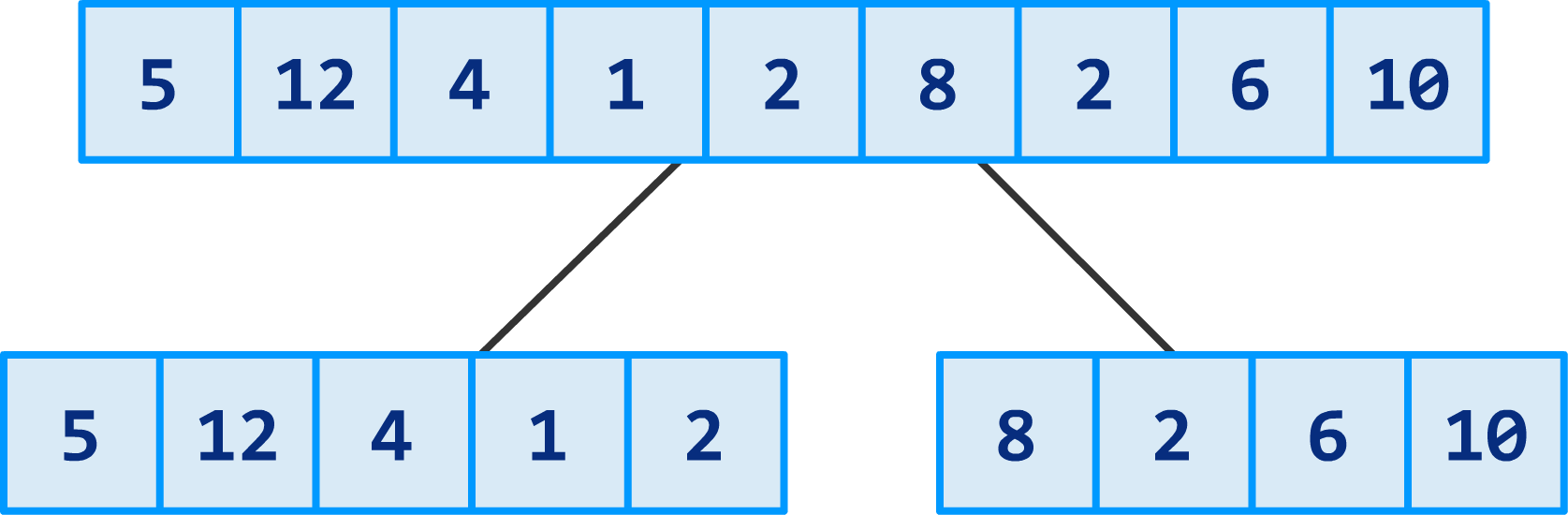
Your original input is now divided into two sections. Next, we continue the dividing by breaking our two sections into four sections:

 

 

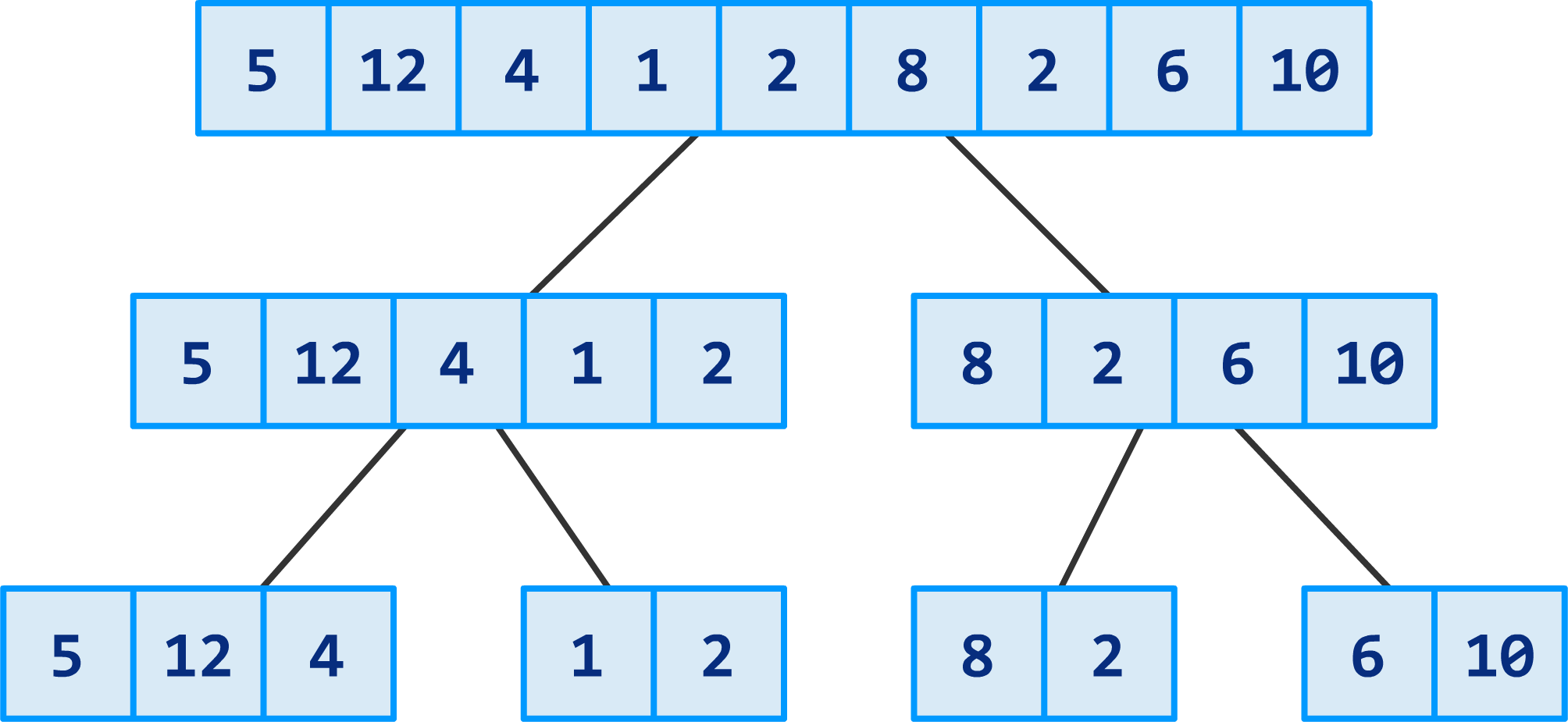
We are going to keep dividing these sections until you get to the point where you are left with just one number in each section and can't divide any further:

 

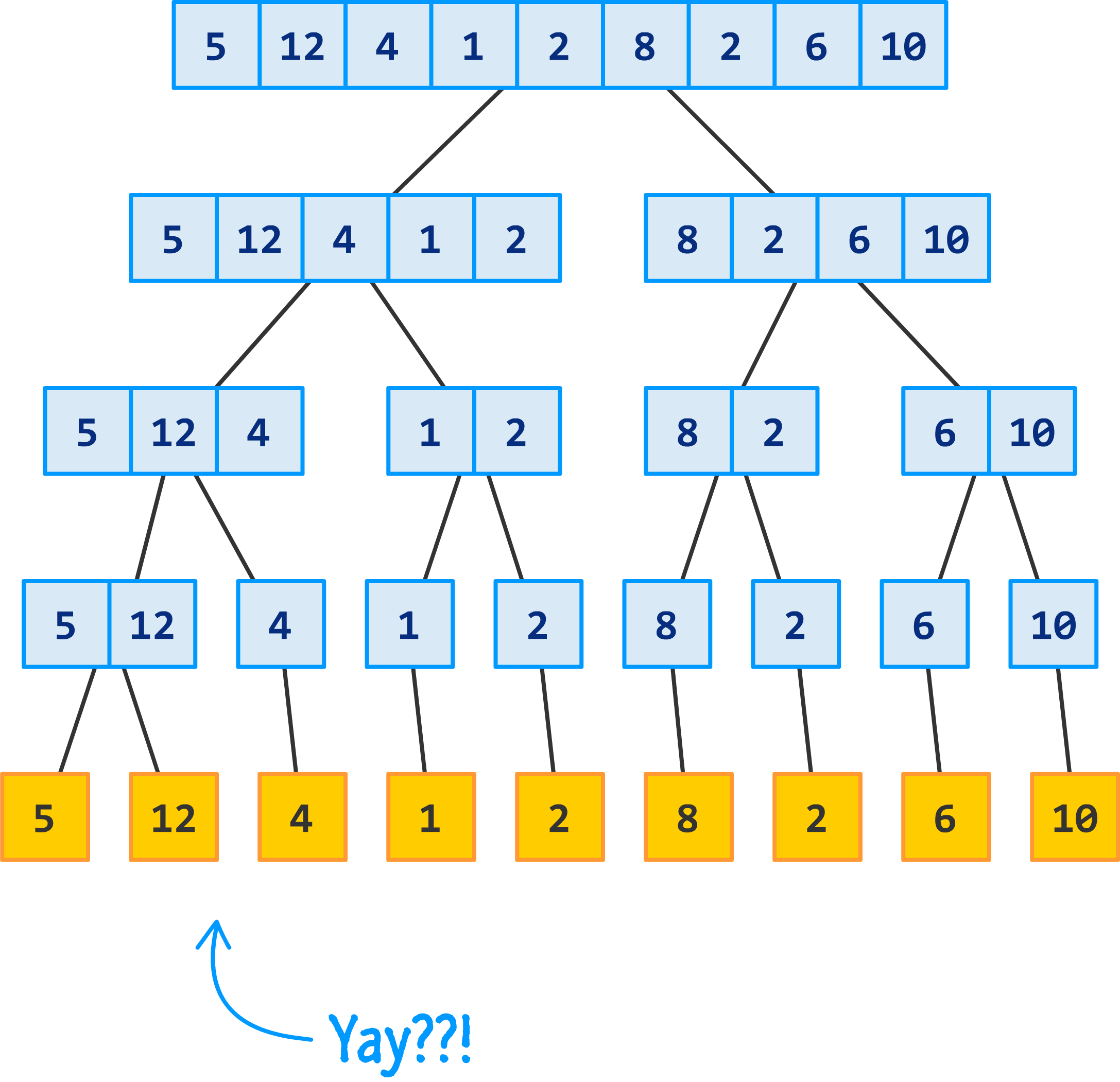
At this point, we have a bunch of individual values that look identical to what we started off with. That's not the goal of what we started out to do, but this is an important part of how mergesort functions. At this stage, we are done dividing. What we are going to see next is a whole lot of merging and sorting...aka the conquering part.

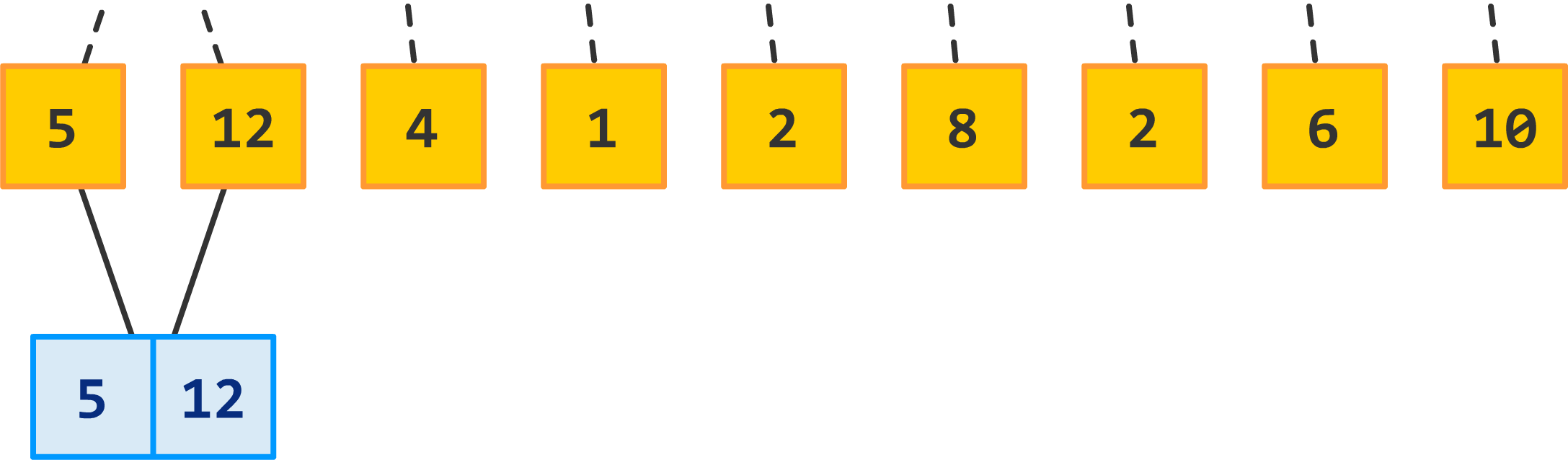
Let's start with the first two sections:

 

 

What we are going to do is merge these numbers together. As part of the merging, we'll also do a sort to ensure the the numbers in the combined section are arranged from smalles to largest. Because we are only dealing with two numbers, this is pretty easy for the 5 and 12:

 

 

We now repeat this for the next two sections made up of the numbers 4 and 1:

 

 

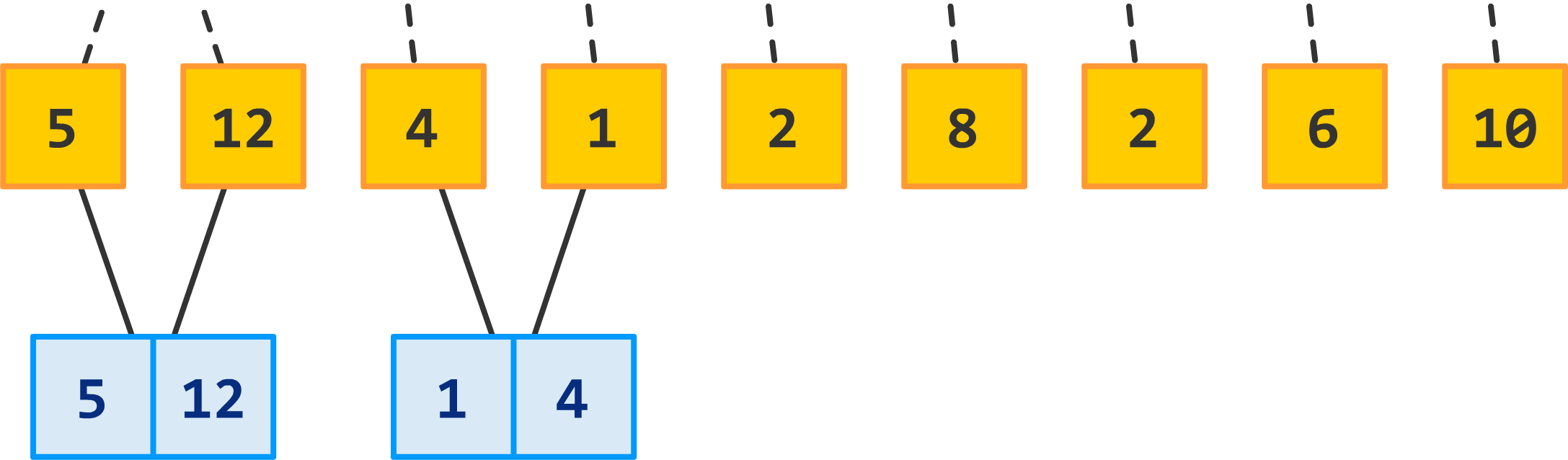
Just like before, we combine the two sections into one section. The sorting part is more clear this time around because the original arrangement wasn't already sorted. We start with a 4 and 1, and the merged arrangement is 1 and 4. Pretty simple so far, right?

Now, we will keep repeating this merge and sort operation on each pair of sections until we run out of sections:

 

 

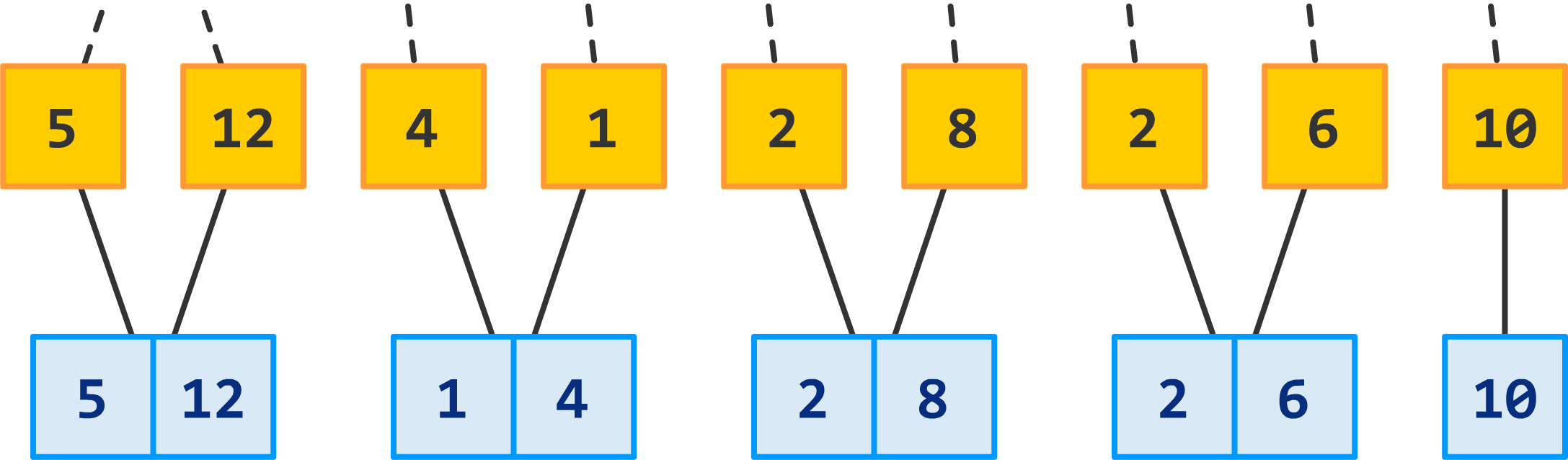
If you have a number that is the odd one and can't be a part of a merge and sort...like our number 10 here, that's OK. Stop making fun of it. We will just carry it along for the next round of merging and sorting and hope its luck improves!

Earlier, we were merging pairs of sections that were made up of one number. That was easy. This time around, we are going to continue merging pairs of sections, but each section will contain two numbers. Take a look:

 

 

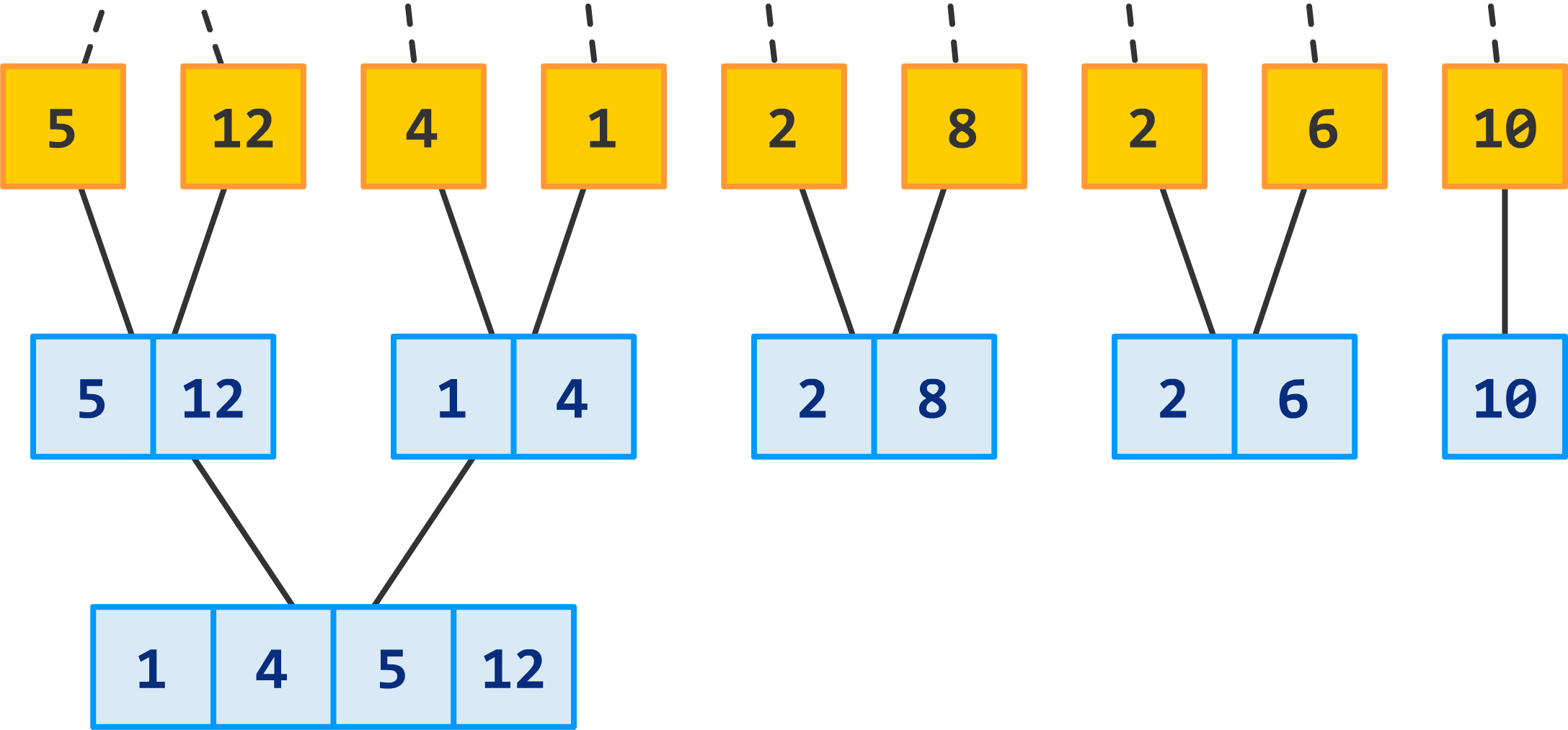
Instead of the merged section containing two numbers, it now contains four numbers...all in perfectly sorted bliss. We repeat this process for the remaining sections as well:

 

 

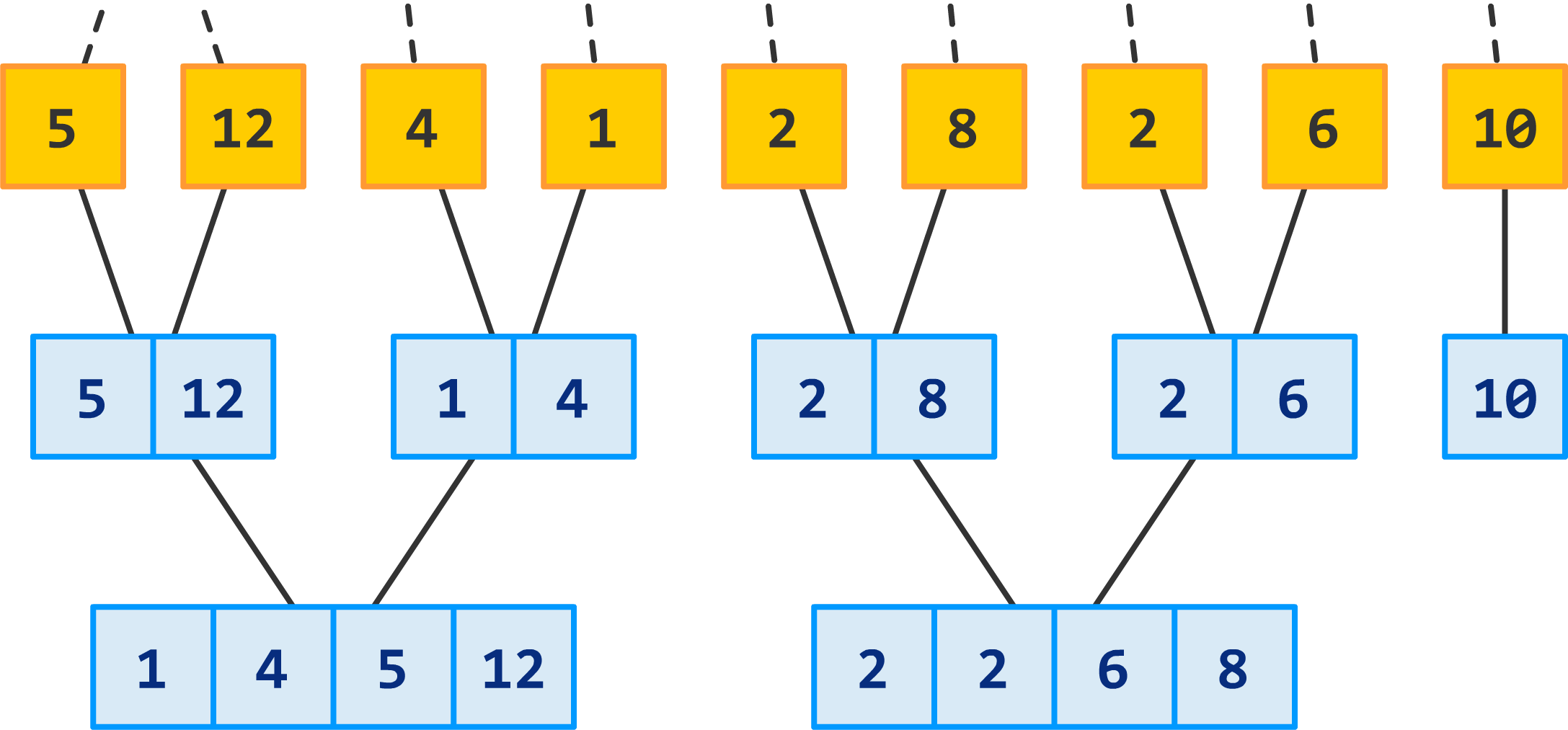
The number 10 is still not quite in the right position to be sorted and merged, so we'll drag it along for the next round:

 

 

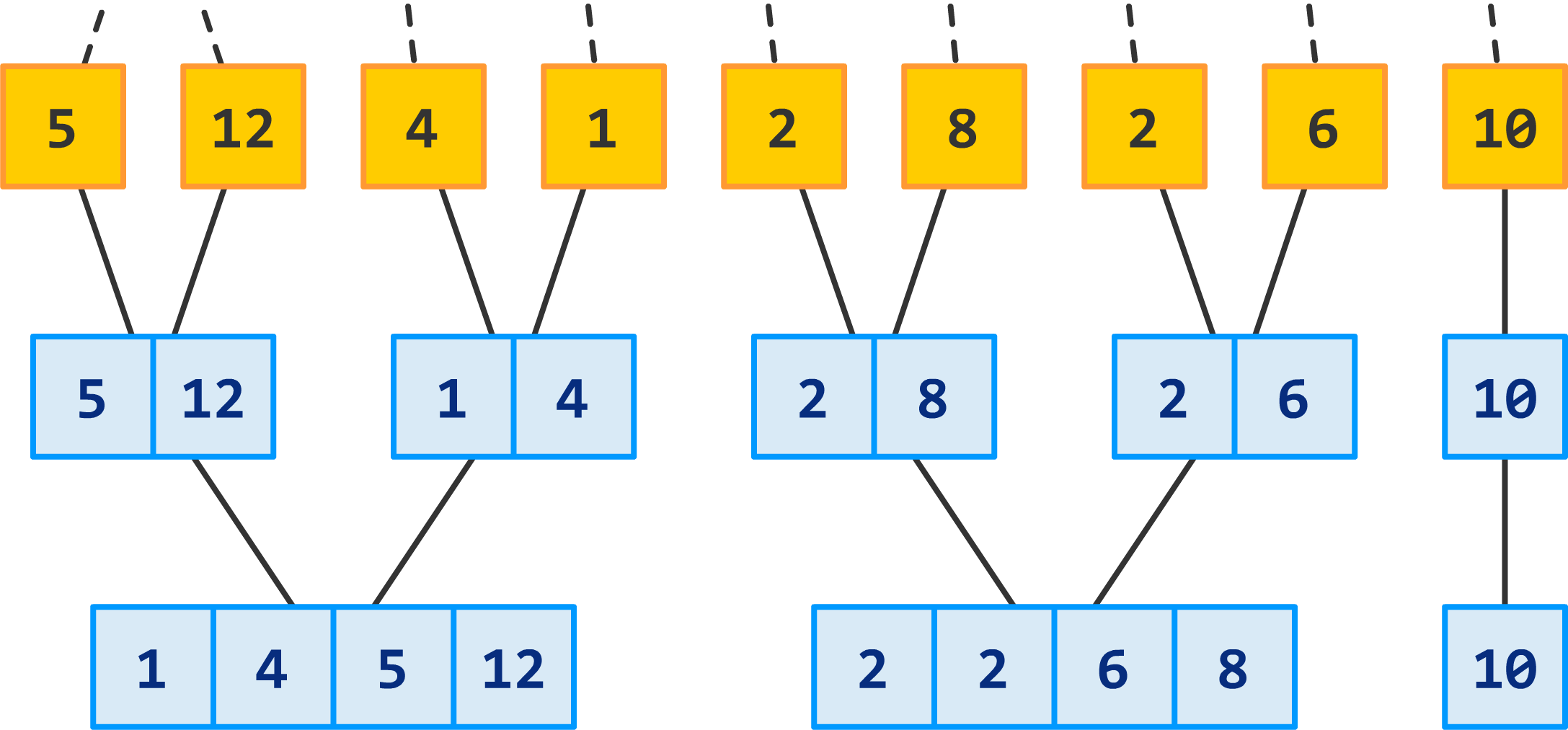
By now, you should start to see a pattern emerge. We are nearing the home stretch here, so let's continue merging and sorting with the next row:

 

 

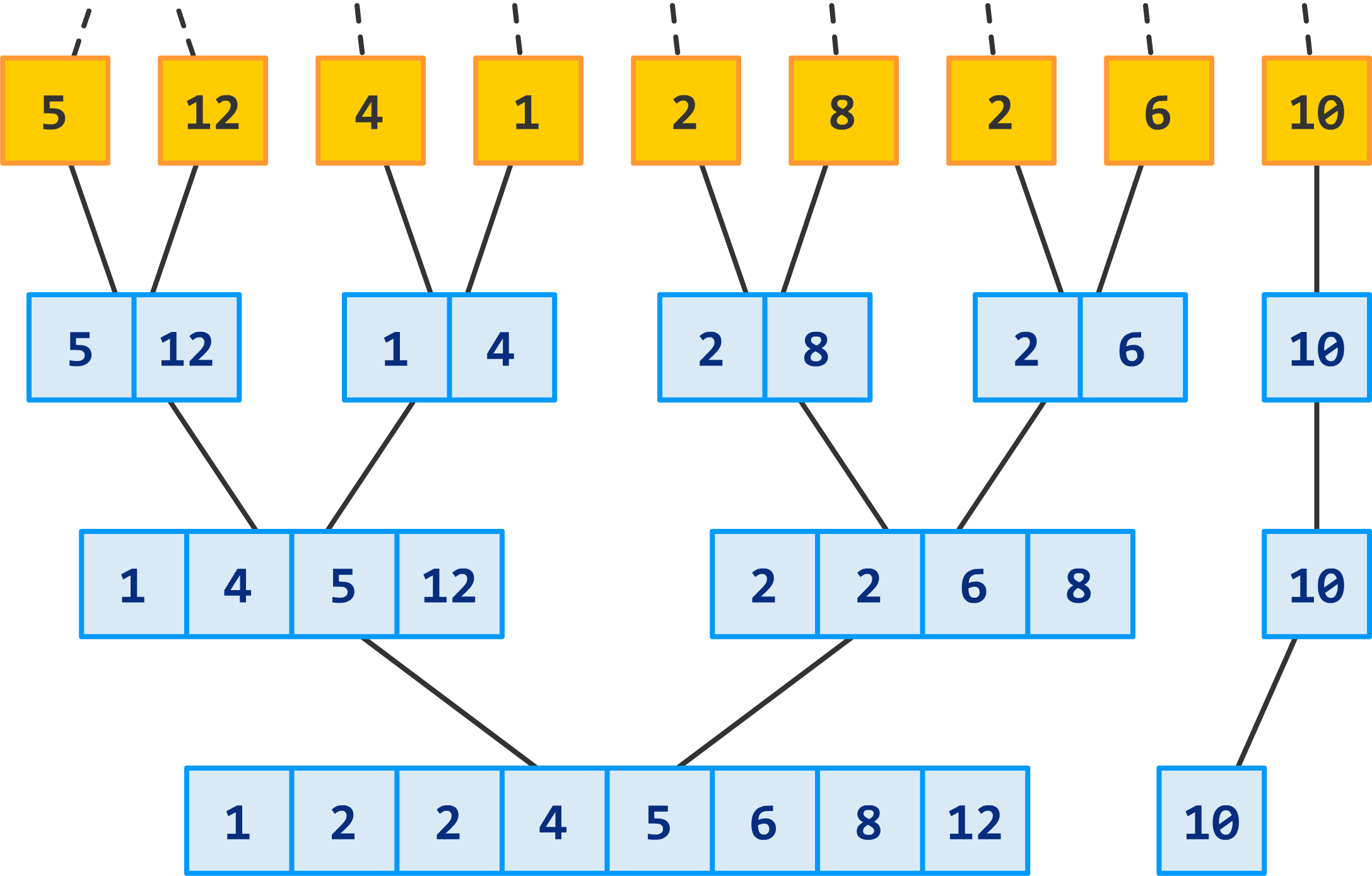
This almost looks fully sorted! We just have one one more round to go, and to those of you deeply worried about the number 10...it makes the cut this time around:

 

 

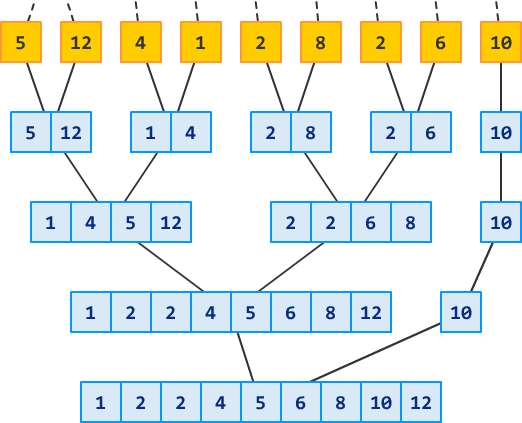
Wohooo! You now have a sorted list of numbers. There are no more sections to merge and sort, so you are done. As a quick recap (and to reminisce about all the good times we had), take a look at the full list of steps we performed to sort our initial collection of numbers:

 

 

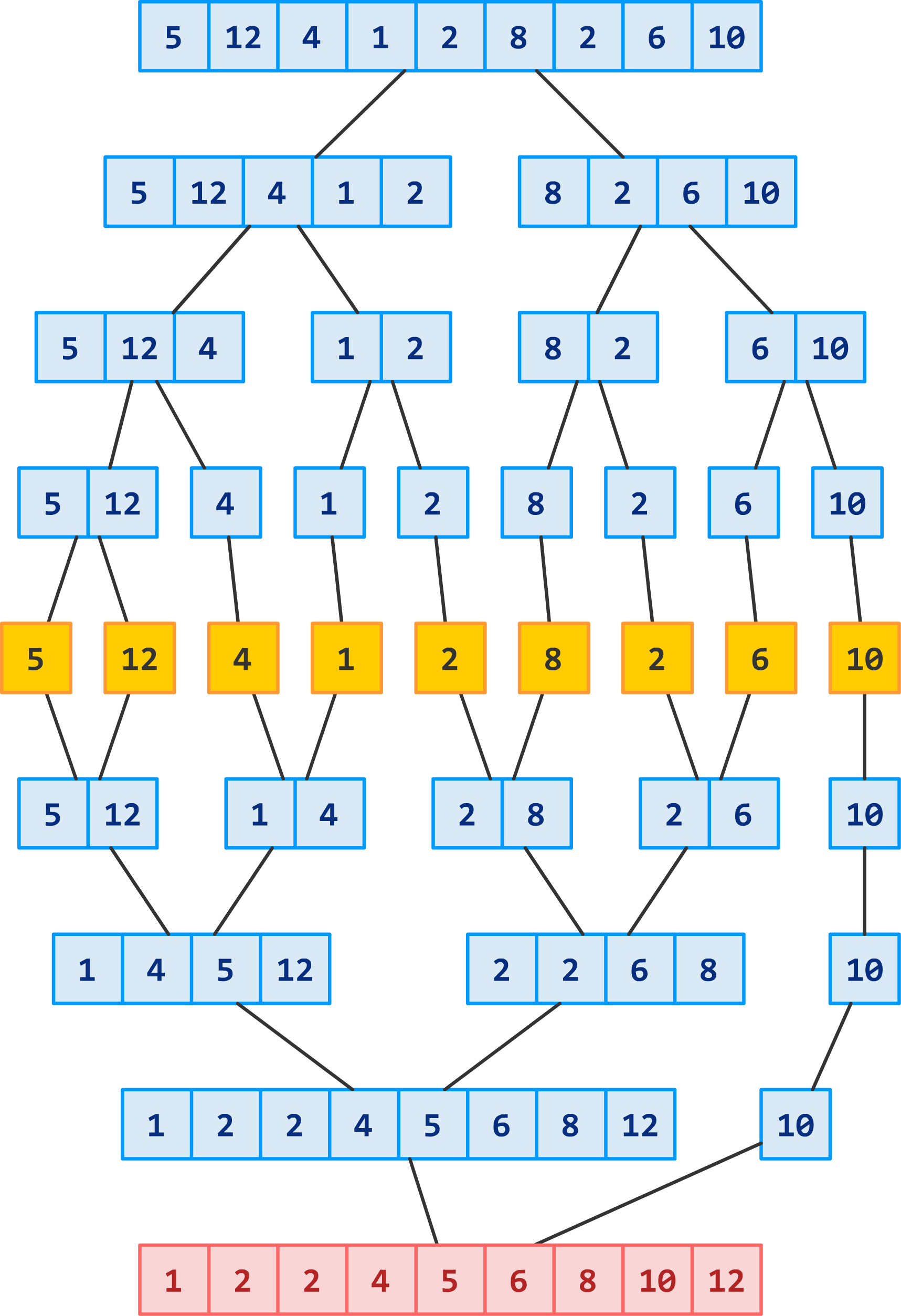
This giant list of steps is a visual representation of mergesort - with all of its dividing and conquering goodness!

Mergesort: The Boring Stuff

The hard part is getting a good handle at how mergesort actually works. If everything in the previous section made sense to you, you are in great shape for the boring (yet important) details that you will need to know in addition. Ignoring all of the diagrams and fancy explanations, mergesort simply does two things:

1. Divides (and divides, and divides, and....) its input into subsections until there is only one element left in each section.
2. Merges (and sorts) all of its subsections back into one big section that is now sorted.

It does all of this in n log n time, and the following tree representation highlights why that is the case:

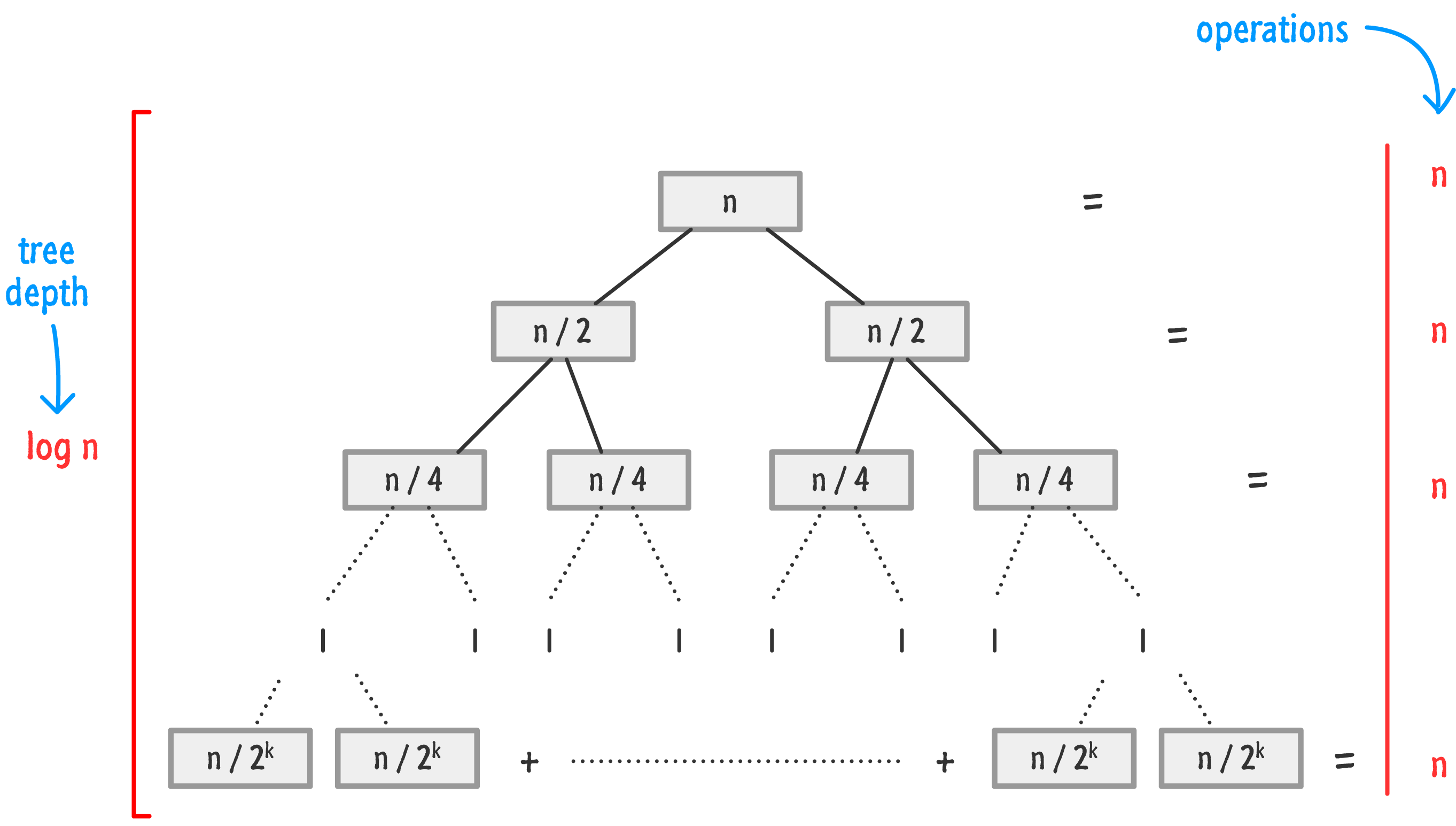
To put in plain English, that is pretty fast and efficient for a sorting algorithm. The depth of your typical mergesort implementation is log n, and the number of operations at each level is n.

When it comes to how much space it takes, things get a little less rosy. Common mergesort implementations take up 2n space in worst case scenarios - which is not terrible, but it is something to keep in mind if you are dealing with sorting within a fixed region of limited memory.

The last detail is that mergesort is a stable sort. This means that the relative order of items is maintained between the original input and the sorted input. That's a good thing if you care about things like this.

Looking at the Code

Now that you've learned how mergesort works and covered some boring details about its complexity, it is time to look at how all of that translates into JavaScript. Below is what my version of the JavaScript implementation looks like:

function mergeSort(input) {
  // just a single lonely item
  if (input.length < 2) {
    return input;
  }

  // divide
  var mid = Math.ceil(input.length / 2);
  var left = mergeSort(input.slice(0, mid));
  var right = mergeSort(input.slice(mid));

  // recursively sort and merge
  return merge(left, right);
}

function merge(left, right) {
  var result = [];

  // order the sublist as part of merging
  while (left.length > 0 && right.length > 0) {
    if (left[0] <= right[0]) {
      result.push(left.shift());
    } else {
      result.push(right.shift());
    }
  }

  // add the remaining items to the result
  while (left.length > 0) {
    result.push(left.shift());
  }

  while (right.length > 0) {
    result.push(right.shift());
  }

  // the sorted sublist
  return result;
}

If you wanted to see this code in action, just call the mergeSort function with an array of numbers as the argument:

var example = [4, 10, 11, 20, 5, 3, 4, 1, -20];
console.log(example);
alert(example);

As you follow through the code, notice that there is absolutely nothing interesting going on here. It's just a lot of loop and array manipulations that make up the divide and merge/sort conquer operations. Now, if you aren't too familiar with how loops and arrays work in JavaScript, then this code is probably just gibberish. To turn this gibberish into something more meaningful, check out my two tutorials on Loops and Arrays!

Conclusion

If you wanted to sort a large list of values, you can't go wrong with using mergesort. It is fast, uses up a reasonable amount of memory, and (unlike quicksort) is stable. Now, before we call it a night and party it up mergesort at the local paintball range, below is a table comparing it with various other popular sorting algorithms and their performance and memory characteristics:

Name	Best	Average	Worst	Memory
Quicksort	n log n	n log n	n2	log n (average)
Mergesort	n log n	n log n	n log n	n (worst case)
Heapsort	n log n	n log n	n log n	1
Tinsort	n	n log n	n log n	n
Bubble sort	n	n2	n2	1
Selection sort	n2	n2	n2	1
Insertion sort	n	n2	n2	1

You can find a more detailed comparison of these sorting algorithms as well as many others over on the Wikipedia section fully dedicated to this.

Just a final word before we wrap up. If you have a question and/or want to be part of a friendly, collaborative community of over 220k other developers like yourself, post on the forums for a quick response!