Earlier, we saw that stacks are are a Last In First Out (LIFO) data structure where items are added and removed from the end. Contrasting that, we have the other popular data structure, the queue. This is an interesting one that we'll learn more about in the following sections.
Onwards!
Meet the Queue
Living up to its name, a queue is very similar to standing in line for something:
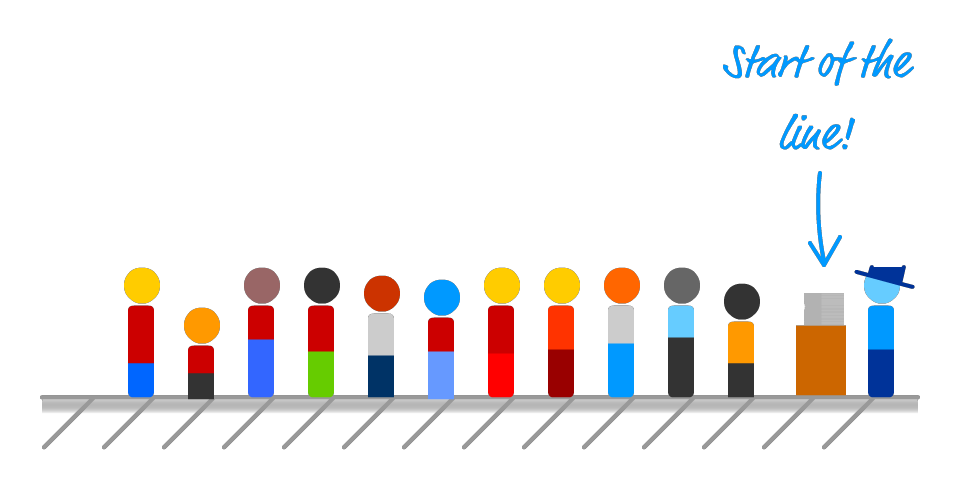
The person standing at the front of the line is the first one to have shown up, and they are the first ones to leave as well. New people show up and stand at the end of the line, and they don't leave until the person in front of them has reached the beginning of the line and has left:
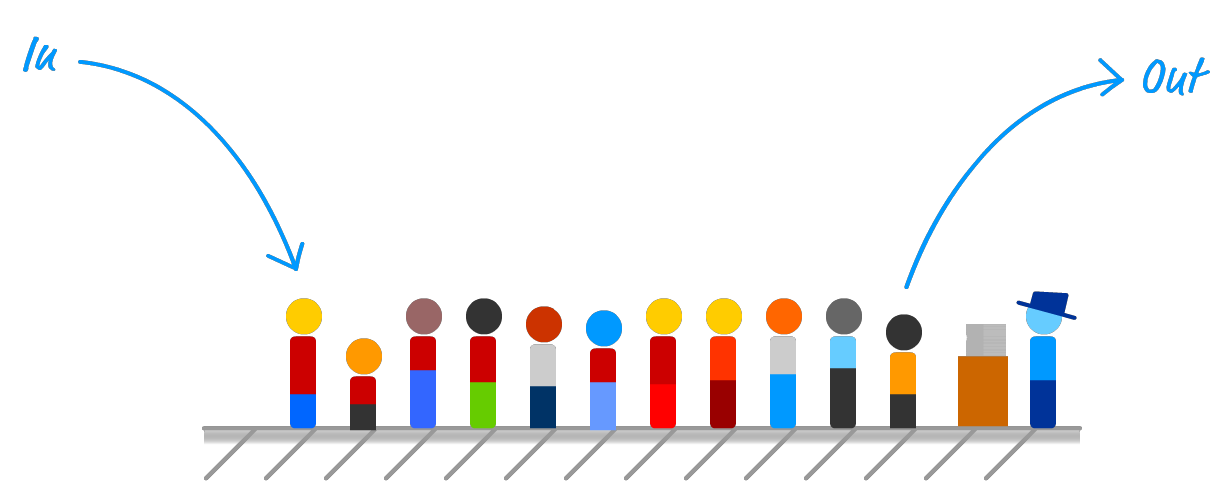
Given that behavior, a queue follows a First In First Out policy more commonly shortened to FIFO. Except for the little big detail about which items get removed first, queues and stacks are pretty similar otherwise.
When adding items, the behavior with stacks is identical:
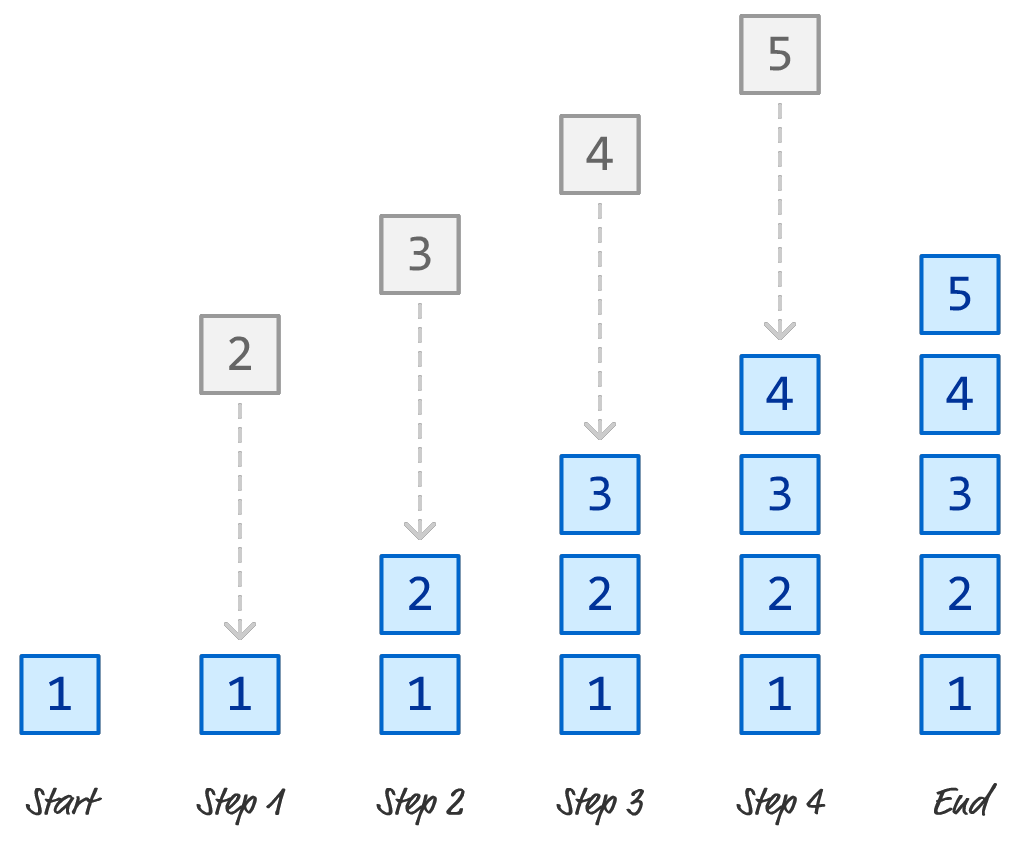
Items are added to the end. When removing items, it is the first item that gets removed in a queue-based world:
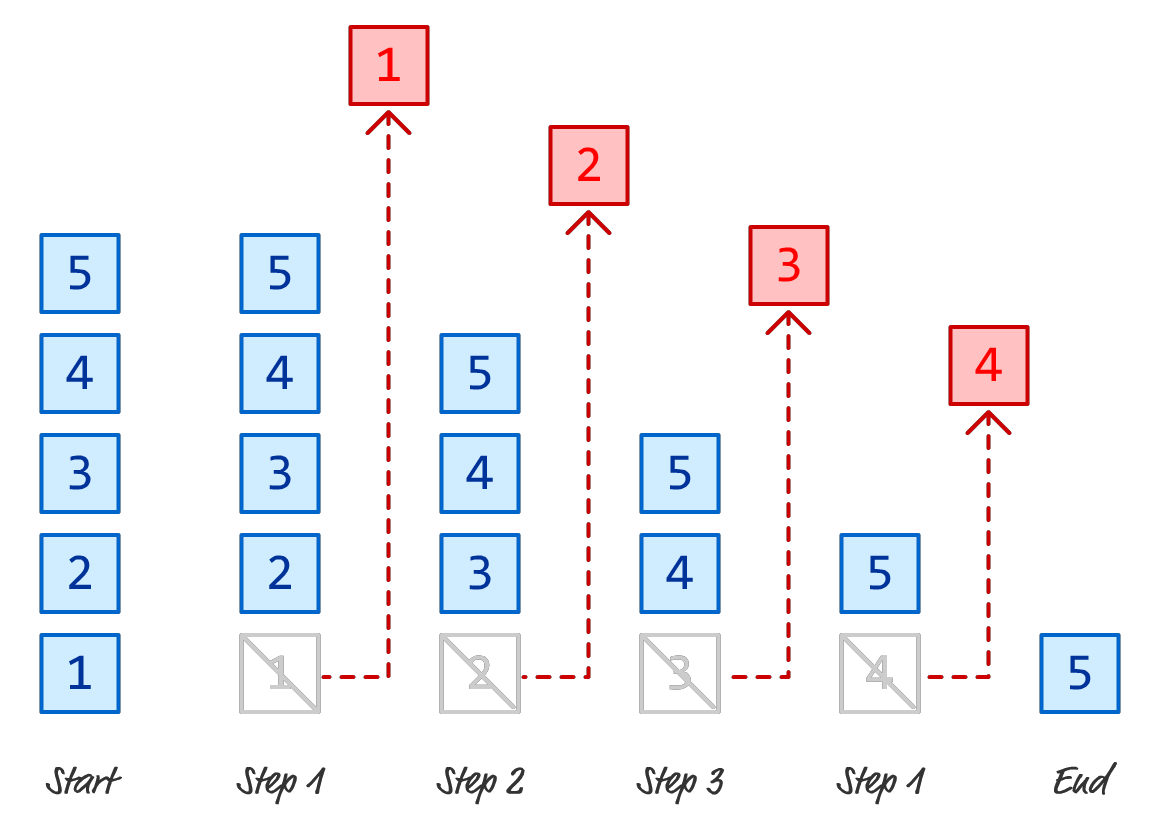
Now, you may be wondering when you'll ever end up needing to use of a queue. Besides helping you appreciate standing in line, queues have a lot of practical uses in the digital world. Pretty much any situation that requires us to maintain an order of something relies on a queue-like data structure. High traffic situations like travel booking, waiting to purchase a ticket for a popular concert, prioritizing e-mails by an e-mail server, and more are all situations where a queue is typically used. We'll see queues used a lot by various algorithms as well, so queues are here to stay! Get friendly with them.
A JavaScript Implementation
To turn all of those words and images into working code, take a look at the following Queue implementation:
class Queue {
constructor() {
this.items = new LinkedList();
}
clear() {
this.items = new LinkedList();
}
contains(item) {
return this.items.contains(item);
}
peek() {
return this.items.head.data;
}
dequeue() {
let removedItem = this.items.head.data;
this.items.removeFirst();
return removedItem;
}
enqueue(item) {
this.items.addLast(item);
}
get length() {
return this.items.length;
}
}Our implementation relies on a Linked List to make some of the data operations much faster (as opposed to just using an Array), so we need to either add our full LinkedList class via copy/paste or reference it from the following URL:
https://www.kirupa.com/js/linkedlist_v1.jsThe way we use a queue is by creating a Queue object, using the enqueue method to add items to the queue, and using the dequeue method to remove items from the queue:
// create new Queue object
let myQ = new Queue();
// add two items
myQ.enqueue("Item 1");
myQ.enqueue("Item 2");
// remove item
let removedItem = my.dequeue(); // returns Item 1We can easily create a copy of our queue by using the clone method, check whether an item exists using contains, and peek at what the removed item might be (without actually removing it) by using...um...peek! The implementation very closely mimics that of our stack, but the important detail is that we are using a Linked List and its implementation along as well.
Queues: Time and Space Complexity
For the most common queue operations, the following table summarizes how our queue performs across common operations:
| Action | Best | Average | Worst |
|---|---|---|---|
| Enqueue (Insert) | O(1) | O(1) | O(1) |
| Dequeue (Remove) | O(1) | O(1) | O(1) |
| Peek | O(1) | O(1) | O(1) |
| Search/Contains | O(1) | O(n) | O(n) |
| Memory | O(n) | O(n) | O(n) |
A key detail for these performance numbers revolves around us using a linked list as the underlying data structure. If we used something like an array, operations that involve modifying the front of our list will take O(n) time as opposed to O(1) time with the linked list. We don't want that! Let's dive a bit deeper into why our queue's performance numbers are what they are.
Runtime Performance
- Enqueue (Insertion): The enqueue operation in a linked list-based queue has a constant time complexity of O(1). This is because elements are added to the rear of the linked list, and there is no need to shift or move existing elements.
- Dequeue (Deletion): The dequeue operation in a linked list-based queue also has a constant time complexity of O(1). Elements are removed from the front of the linked list, and like the enqueue operation, no shifting of elements is required.
- Peek: The peek operation, which allows us to access the front element without removing it, is also an O(1) operation. It directly retrieves the value from the head of the linked list.
- Search: Searching for an element in a linked list-based queue is less efficient than its insertion or deletion operations. The search operation requires traversing the linked list from the front to the rear, resulting in a linear time complexity of O(n), where n is the number of elements in the queue.
Memory Performance
The overall memory usage of a queue is O(n) where each element in the queue is represented by a node, which contains the data and a pointer/reference to the next node. Therefore, the space required grows linearly with the number of elements in the queue.and the following are some details to keep in mind. With that said, there are a few additional details to keep in mind:
- Dynamic Memory Allocation: Linked lists are dynamically allocated, meaning that memory is allocated for each node as elements are added to the queue. This allows the queue to dynamically resize and efficiently handle varying numbers of elements.
- Memory Overhead: Linked lists require additional memory for maintaining the pointers between nodes. We know that already! This overhead, compared to an array-based implementation, can be a disadvantage when dealing with a large number of small elements.
- Cache Performance: Linked lists can suffer from cache performance issues because the elements are not stored in contiguous memory locations. This might lead to more cache misses, affecting the overall performance for certain operations.
Not too shabby, right? A queue implemented using a Linked List provides efficient insertion and deletion operations with a constant time complexity of O(1). Searching for an element in the queue is slower with a linear time complexity of O(n). When it comes to memory, things are pretty consistent with a linear O(n) growth based on the number of items our queue is storing.
Conclusion
Between what we saw earlier with Stacks and what we saw just now with Queues, we covered two the most popular data structures that mimic how we model data enters and leaves. A queue is known as a FIFO data structure where items get added to the end but removed from the beginning. This "removed from the beginning" part is where our reliance on a linked list data structure comes in. Arrays, as we have seen a few times, are not very efficient when it comes to removing or adding items at the front.
Just a final word before we wrap up. If you have a question and/or want to be part of a friendly, collaborative community of over 220k other developers like yourself, post on the forums for a quick response!
