The Monty Hall Problem is a puzzle loosely based on the premise of the popular game show Let's Make a Deal, which was hosted by Monty Hall. We'll go into more detail on how the game is played, but the inherent conflict in the game comes from a situation where the contestants have less information than they need to craft a winning strategy.

This is one of those games whose winning strategy has puzzled and divided people for years, sparking heated debates and lively discussions among mathematicians, statisticians, Twitteratis (or X-eratis), and game show enthusiasts alike. Even though the solution may seem counterintuitive at first, we'll walk through the logic together and explore the probabilities involved.

Onwards!

How the game is played!

When a contestant walks onto the stage where the Monty Hall Problem takes place, they'll immediately be greeted by three doors:

Behind one of the doors is an item of high-value. Behind the other two doors is an item of low value:

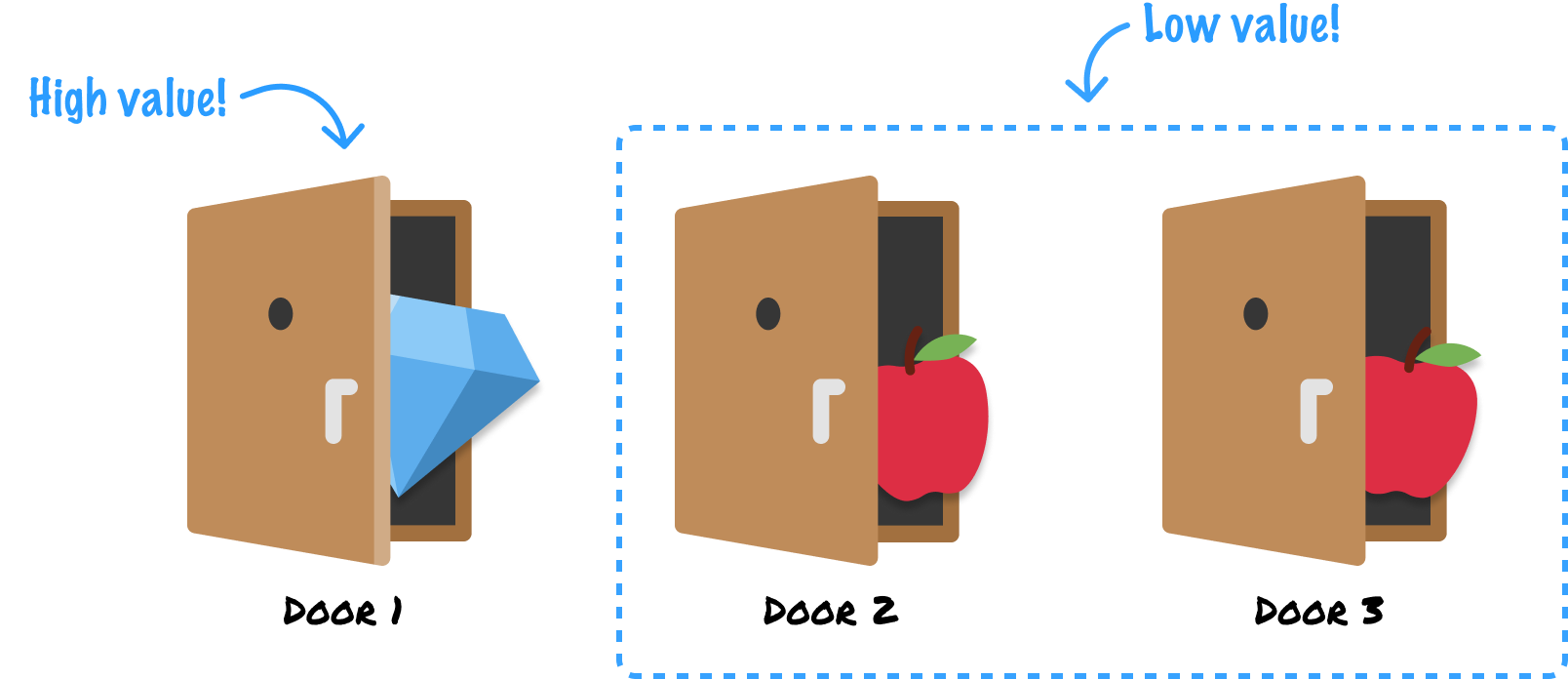
The part that makes this interesting is that the contestant has no idea what is behind any of the doors. There are no clues or signals that can help the contestant make an informed choice on which door contains the high-value item. It could be any of them:

Armed with zero knowledge, the contestant has to randomly pick a door that they think has a high-value item in it. For example, they may pick Door 2:

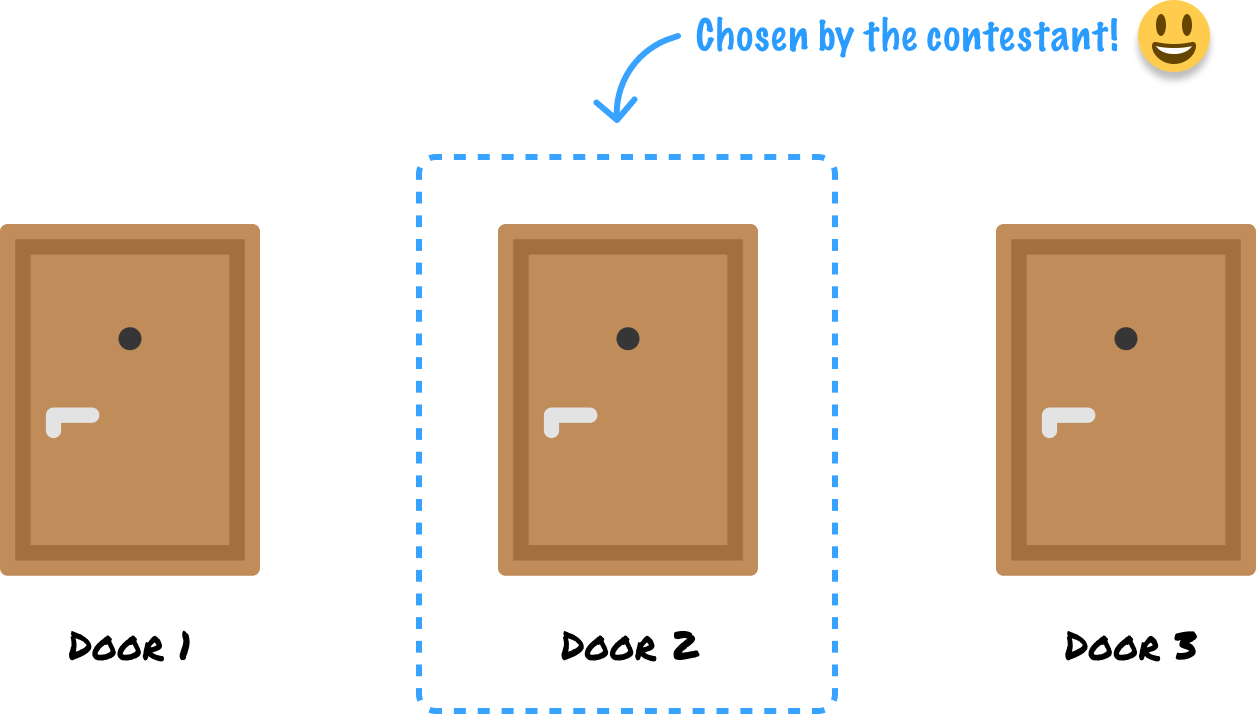
This leaves behind Doors 1 and 3. Monty, unlike the contestant, knows what is behind all of the doors. For example, he knows that Door 1 has the high-value item in it. He also knows that Doors 2 and 3 have low-value items in them. What he does next is give the contestant a hint. He reveals what is behind one of the doors using the following criteria:

1. The contestant didn't select this door
2. This door has a low-value item in it

Based on this, Monty exposes what is behind Door 3:

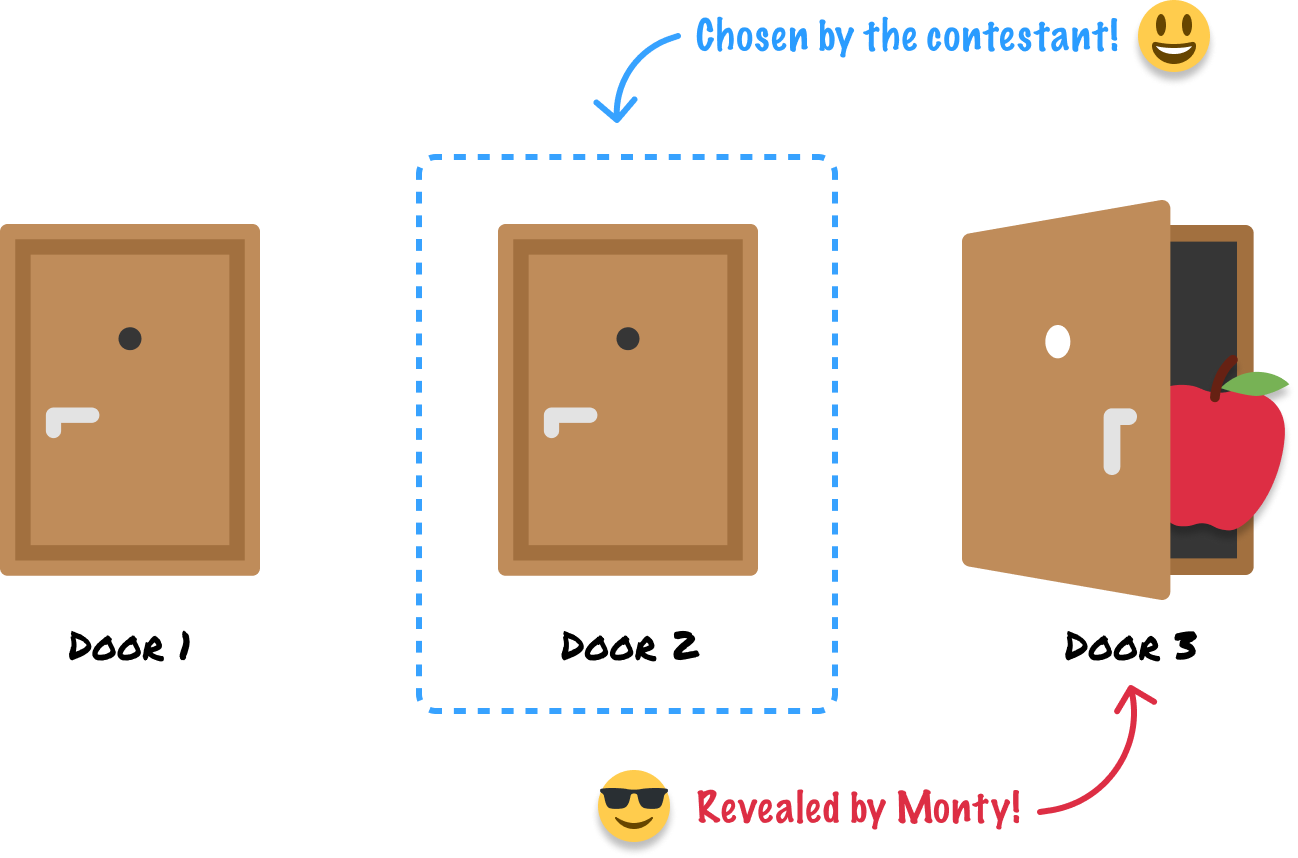
Remember, the contestant chose Door 2. The high-value item is in Door 1. The only door that Monty can reveal to keep the game going is Door 3. Monty will never reveal the door with a high-value item, for that would end the game in a pretty anticlimactic way.

The contestant now has added information that they didn't have when making their initial selection. Thanks to Monty's reveal, the high-value item is definitely not in Door 3. The high-value item is now either in Door 1 or, the door the contestant chose, Door 2. At this point, Monty offers the contestant a choice:

Do you want to stick with your current selection of Door 2, or do you want to switch your selection to Door 1?

What should the contestant do? Do they stick with their initial choice of Door 2. Or do they switch to the other remaining door, Door 1? Dealing with this conundrum is the source of the Monty Hall Problem.

Thinking About Probabilities

Before we talk about what the contestant should do, let's take a few steps back. When we first encounter this game, we can reasonably state that the probability that one of the doors has a high-value item is one-third (1/3 or ~33%). When the contestant makes a selection, they are making it with no real information. They are just guessing. This means they randomly select a door hoping that it has a high-value item behind it.

In selecting one door, our contestant leaves two doors unselected. At this stage of the game, it is just as likely that one of the two unselected doors has a high-value item behind it instead:

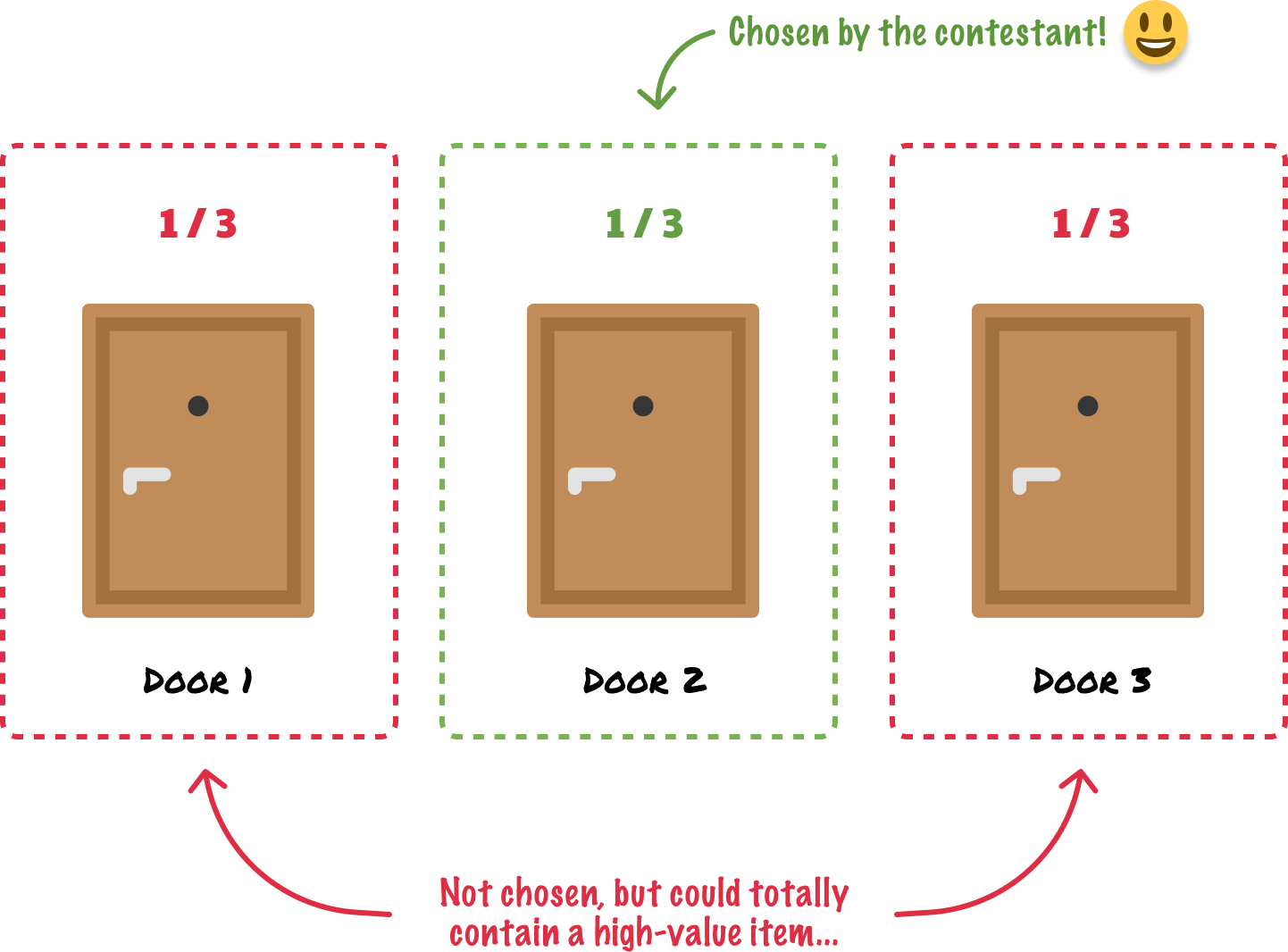
It's hard to know. We are all just guessing after all. So far, our contestant has a one-third chance of having chosen the door with a high-value item. There is a two-thirds (2/3 or ~66%) chance that one of the unchosen two doors has a high-value item in it instead. Take a moment to mentally visualize this situation.

Now, this is where Monty steps in. He does his big reveal and shows that Door 3, one of the doors that the contestant didn't select, has a low-value item in it:

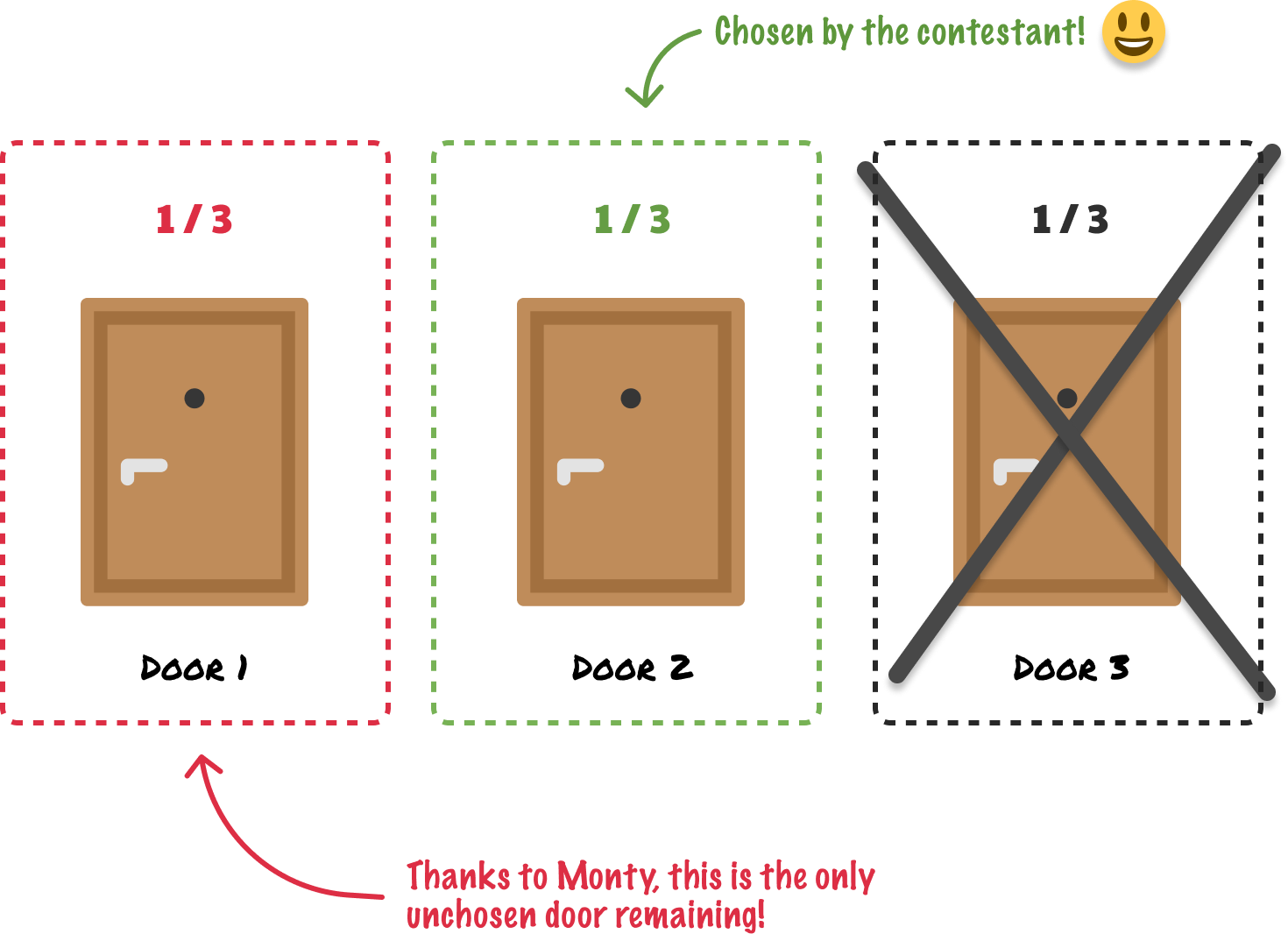
What does this do to our earlier probability, where we said that there is a two-thirds chance that the high-value item is behind one of the doors we didn't select? The probability remains unchanged. There is a two-thirds chance that the high-value item is behind Door 1. That seems counterintuitive, right? Let's dive deeper into why that is the case by looking at a variation of this game involving more doors.

Instead of playing the game with three doors, we now have twenty doors:

The rules of this twenty-door variation are still the same. The contestant picks one door, Monty reveals what is behind all but one of the unselected low-value doors, and the contestant has to decide whether to stay with their original pick or switch to the door Monty indirectly selected by process of elimination.

For this game, let's say that the high-value item is located at the following location:

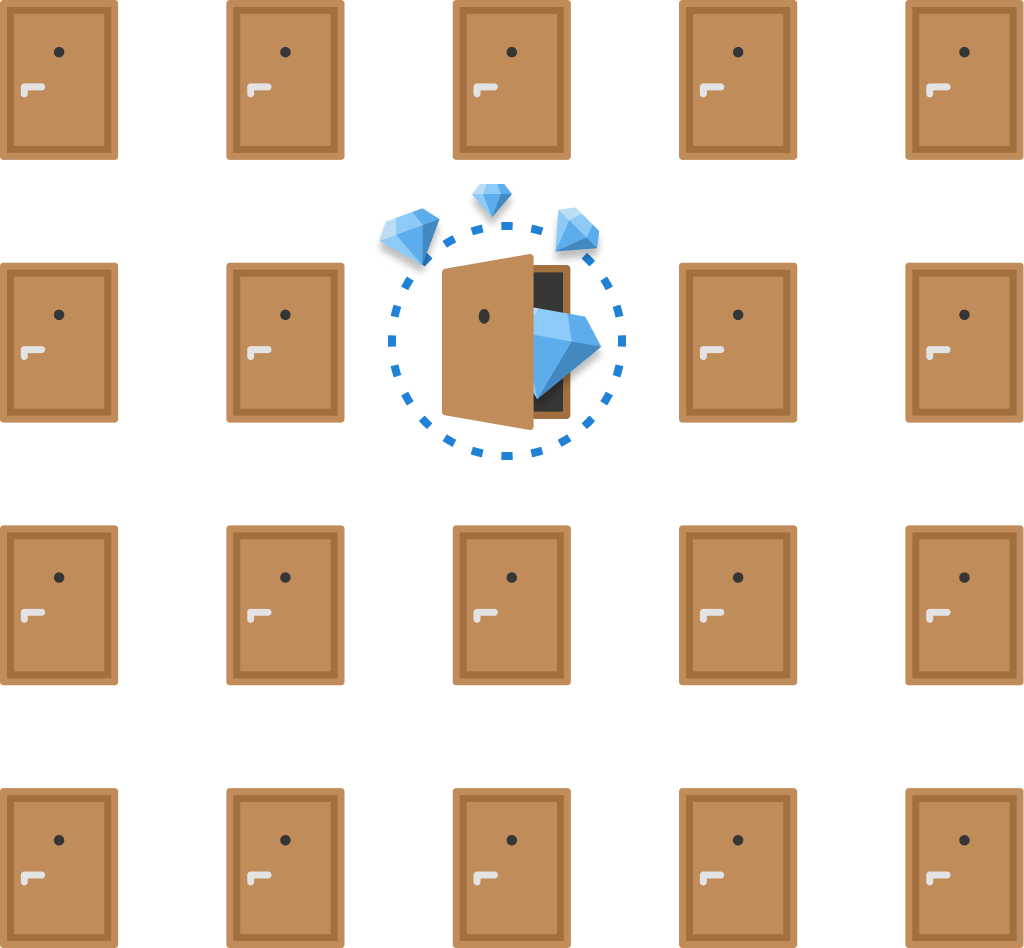
Remember, the contestant has no idea about where the high-value item is located. The only people who know where the high-value item is located are you, me, and Monty.

Getting back to the game, the contestant picks the first door as being the one they think has a high-value item inside it:

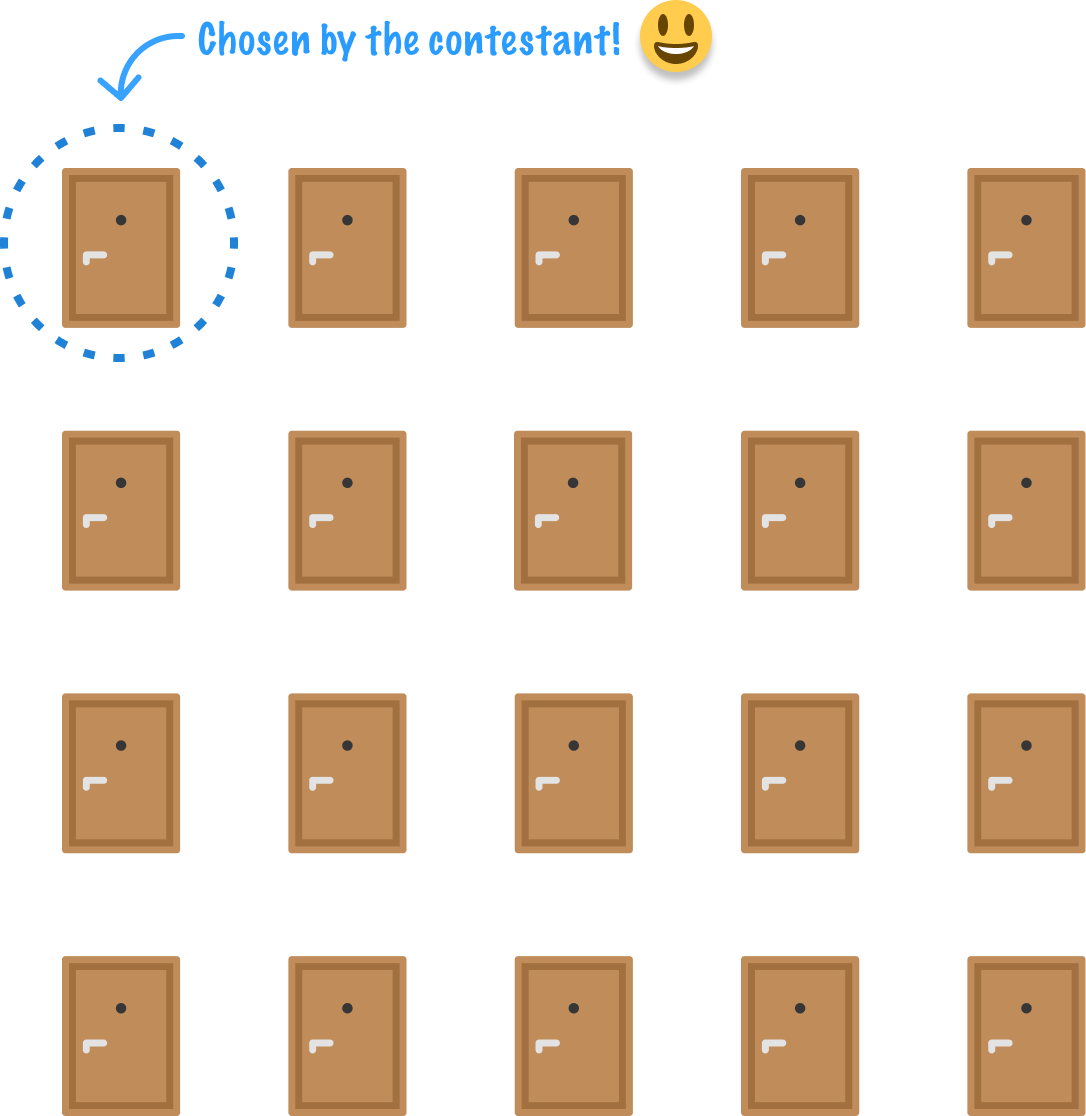
Using the same probability approach that we saw with the three doors variation of the game, the chances that the contestant's selected door hides a high-value item behind it is one out of twenty (1 / 20 or 5%). This means that there is a nineteen out of twenty (19 / 20 or 95%) chance that the high-value item is in one of the doors the contestant didn't select:

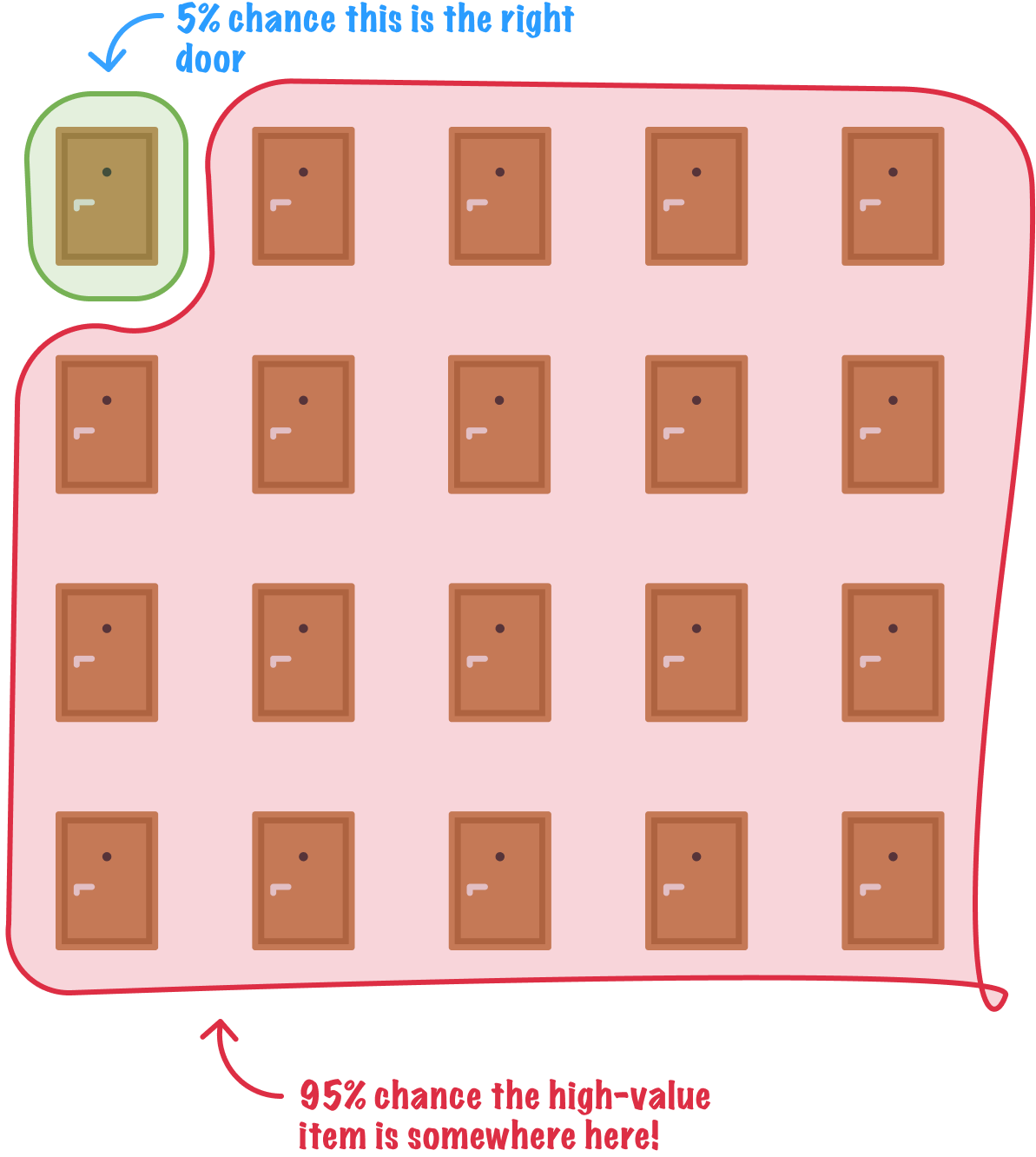
Our good friend Marty re-enters this game. He goes through all the unselected doors and reveals all the low-value ones (except for one):

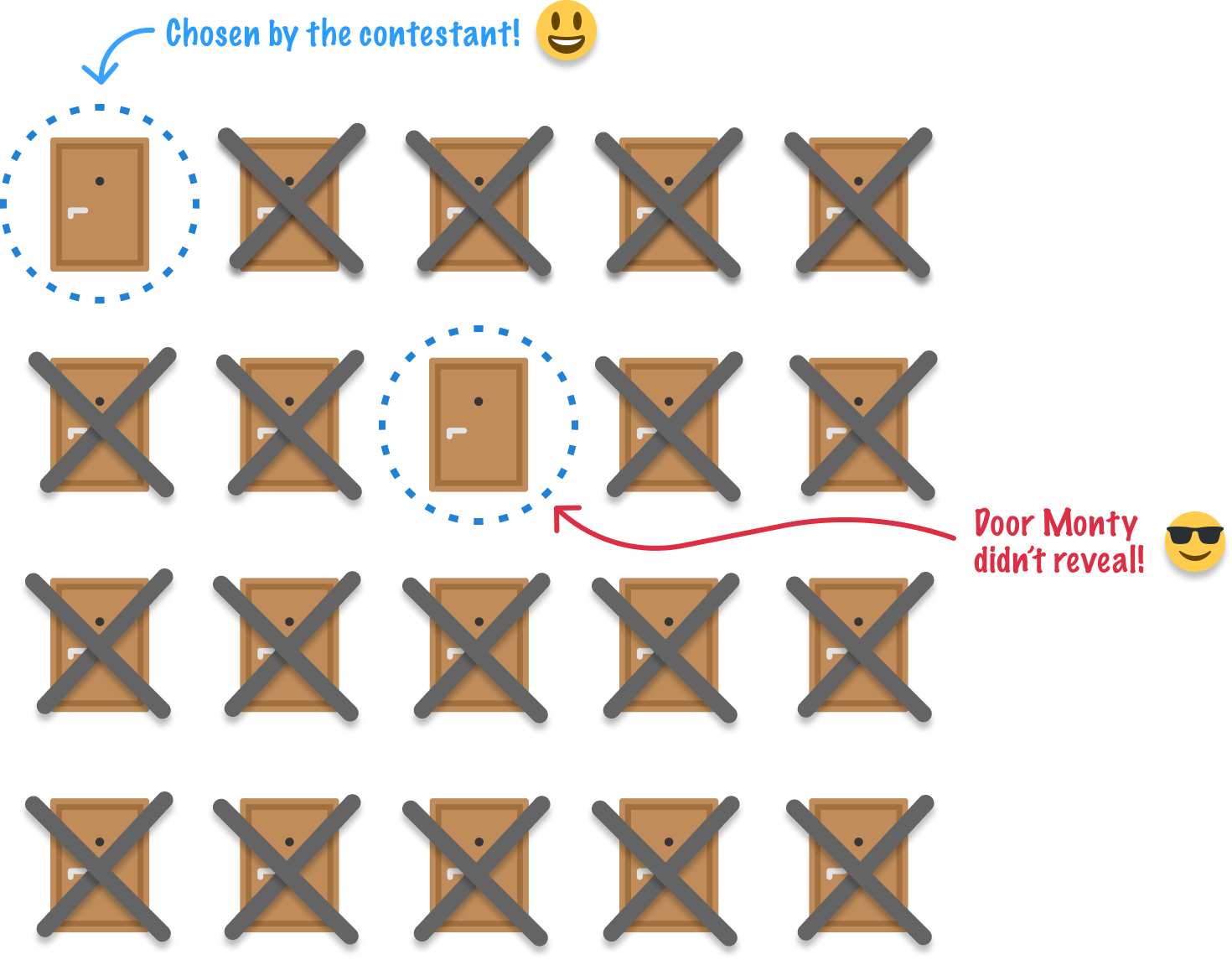
The door Monty doesn't reveal is the one that contains our high-value item. Again, our contestant doesn't know that. At this point, Monty asks the contestant his classic question:

Do you want to stick with your current selection, or do you want to switch your selection to the other door?

What should the contestant do? There is a winning strategy here. The contestant should always switch. It isn't often the word always shows up in probabilities, but this is one of those cases. In the following section, we'll learn why.

Why You Should Always Switch

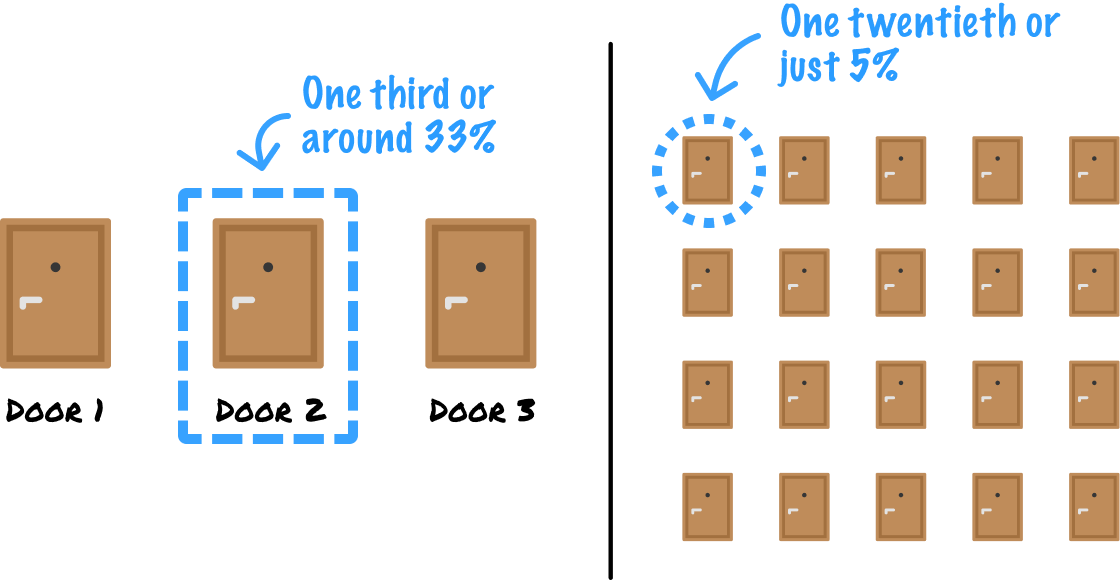
When situations are truly random, our choices aren't going to be well-informed. We would pick randomly, expecting a random outcome. What we see with the Monty Hall problem is something that starts off as a random guessing game. The probability that our contestant selects a high-value door is one-third (1 / 3 or ~33%) for our original three-door variation, and one-twentieth (1 / 20 or 5%) for our twenty-door variation:

The game changes once, of the remaining unselected doors, Monty reveals all low-value doors except for one. What we have now is a selected door and an unselected door:

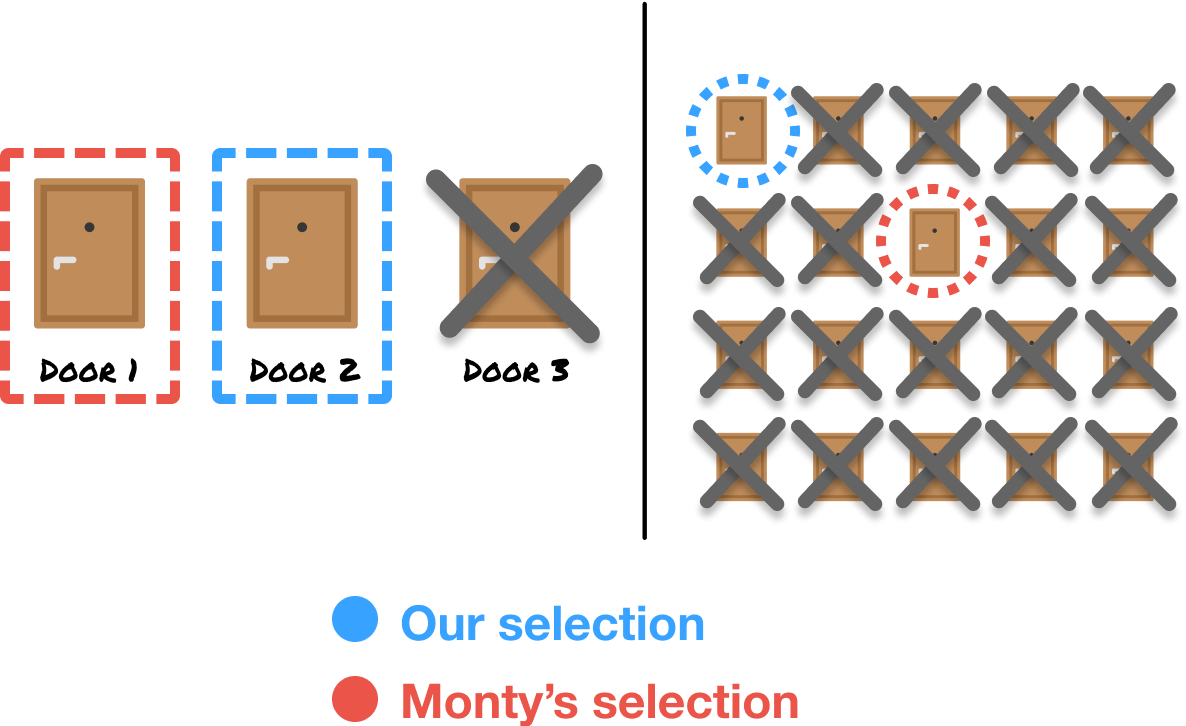
The mistake is to think that the probability of the remaining unselected door returns to being one-third or one-twentieth, just like it was during the initial selection.

The reason why that isn't the case is because the contestant has more information to help them make an educated selection. They are no longer choosing randomly. After Monty reveals the low-value doors, what he essentially did was eliminate a bunch of bad choices. Out of three doors, one door was eliminated because it housed a low-value item. Out of twenty doors, eighteen doors were eliminated for housing low-value items.

At the start of the game, we kinda knew the game was rigged against the contestant. Even if the contestant selected a door, the probability of our high-value item being in one of the doors the contestant didn't select was much higher. For our three-door variation, the probability that one of the unselected doors housed a high-value item was at two-thirds or around 66%. For our twenty-door variation, the probability rose to nineteen out of twenty or 95%.

When Monty reveals all but one of the unselected doors as having a low-value item, he concentrates the probability onto the door that he indirectly selects for us. This means that the remaining unselected door, thanks to Monty, has a much higher probability of storing our high-value item than the door the contestant selected initially:

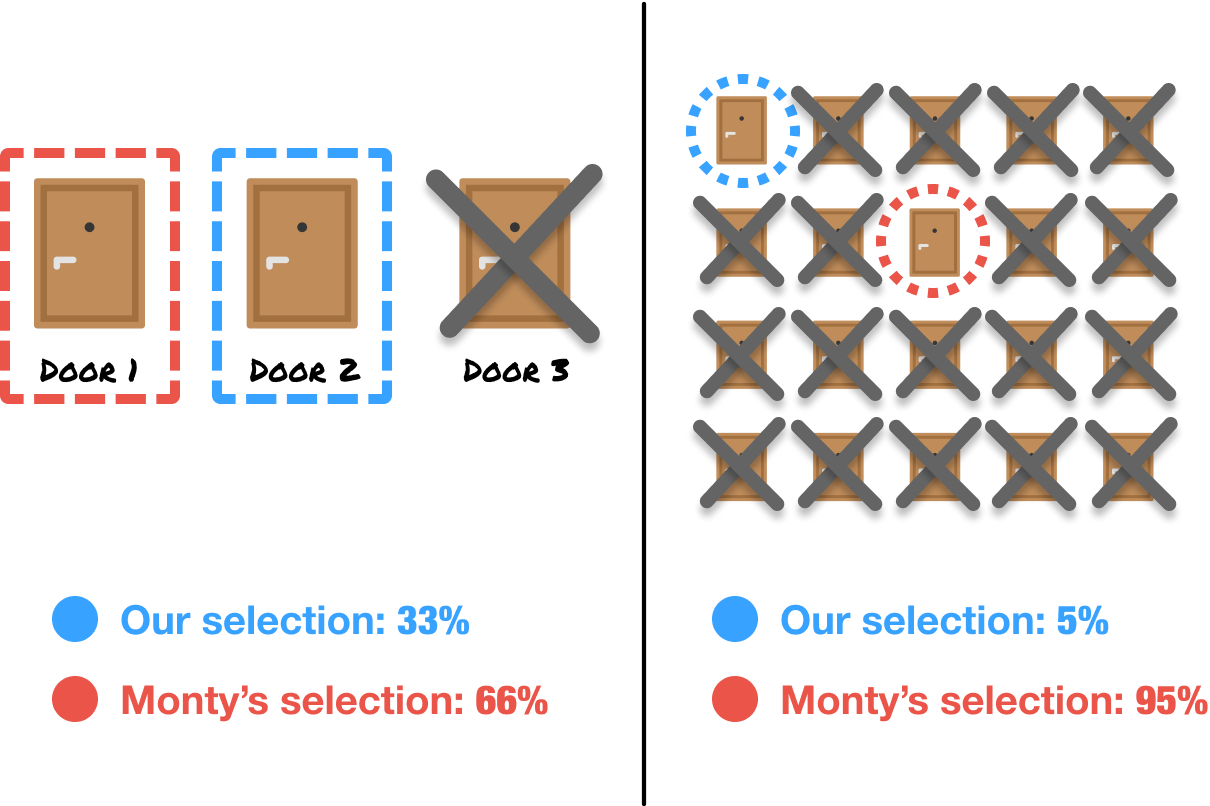
This is why, when faced with a similar situation, we should always switch to the door Monty provides as an alternative to what we originally chose. The probabilities are heavily in favor of the switcher.

Conclusion

As numerical reasoning exercises go, the Monty Hall problem is one of the most popular ones for a few reasons. The rules of the game are simple: pick a door, wait for Monty to clear the field, and decide whether to either stick with the original door or switch to the unselected door Monty presents you with. That's it. The simplicity of the rules hides a series of interesting thought experiments that mathematically lead to one strategy: always switch to the door Monty provides for you. If you are still unconvinced, we can even run a simulation to see why switching is best! 🎲

Just a final word before we wrap up. If you have a question and/or want to be part of a friendly, collaborative community of over 220k other developers like yourself, post on the forums for a quick response!