Learn three ways to calculate pi (π) with varying degrees of speed and accuracy using JavaScript!
Today, we know that the value of pi is around 3.14. Let’s take a step back for a moment. How did we arrive at this value for pi? The answer to this is rooted in thousands of years of history where, for a really REALLY long time, we have been trying to figure out what the value of pi is via a bunch of clever and cutting-edge techniques.
Originally, they way we calculated PI was by taking a circle and measuring two things:
If we had to visualize those two things, it would look a little something like the following:
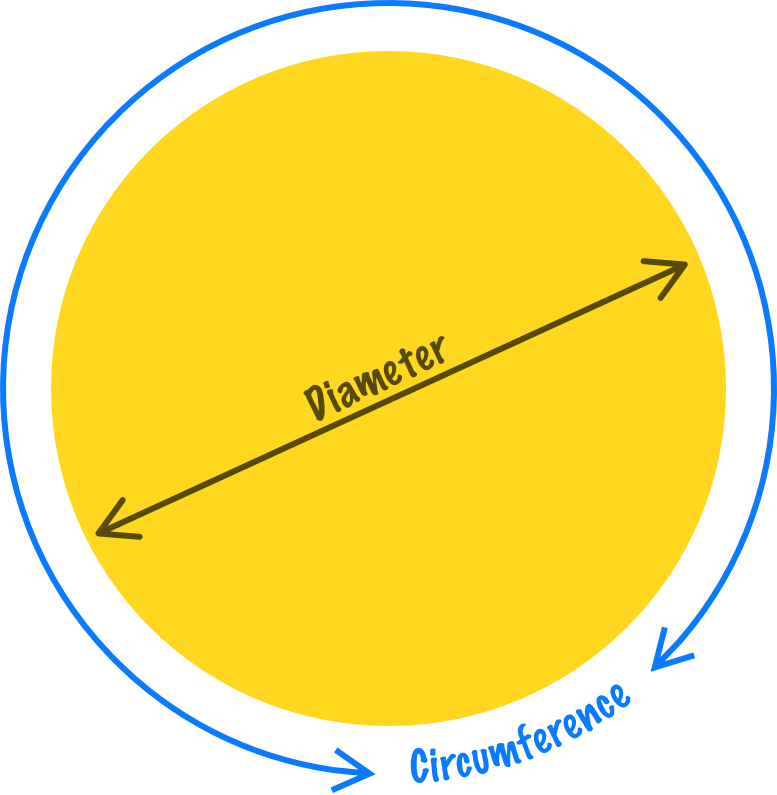
With these two important details chalked out, what people found is that the ratio between the circumference and the diameter turned out to be a constant value. This value never changed no matter the size of the circle. This constant value became cemented as the greek letter, π or commonly referred to as pi in English:
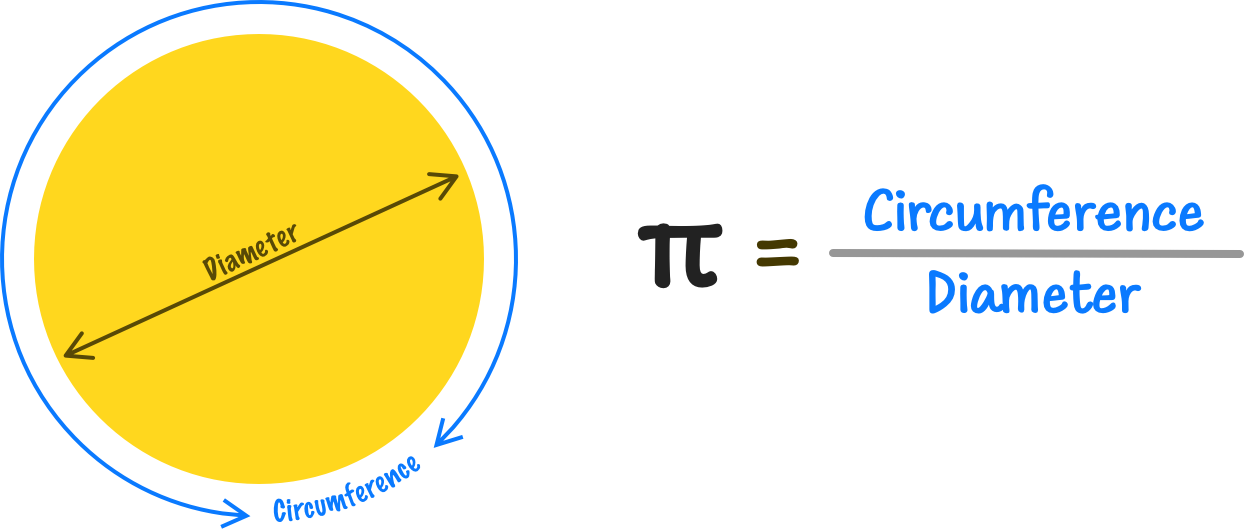
The value for pi got more precise as time went on and people developed better techniques for calculating its true value. This is highlighted by the following visual from Google:
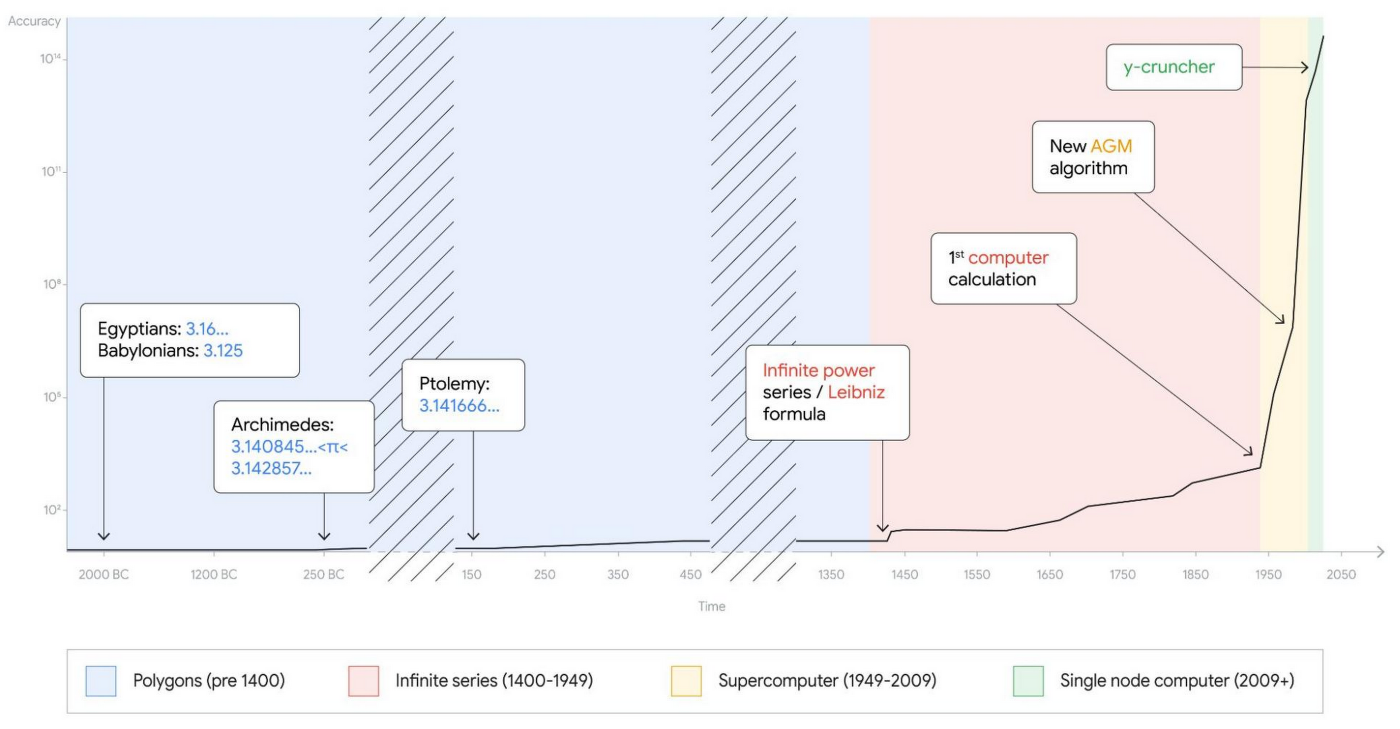
Notice that each major increase in the precision of pi was marked by some major technical advancement such as better ways to take measurements, new mathematical techniques, or the invention of the computer.
What we are going to do in this article is look at a few popular approaches for calculating pi and reimplement them ourselves in JavaScript. This is going to be a fun activity that ties together some of the more basic JavaScript concepts around functions, looping, console logging, and mathematical operators.
Onwards!
Before I go too far here, if you are here to just get a value of pi that you can use in your JavaScript apps, you have ready access to that by using the Math.PI constant:
console.log(Math.PI); // 3.141592653589793This will give you a version accurate enough to use for most calculations. If this is what you were looking for, the rest of the content here is around how we can generate this value ourselves. Now, if you are down for learning how to calculate pi using some common techniques spanning all the way from 2000 years ago to more modern times, read on!
The earliest approaches for calculating pi were of the geometric kind by Archimedes. While measuring the circumference of a circle accurately was tricky, measuring the perimeter of shape with straight lines that we could easily measure like a polygon was not very tricky:
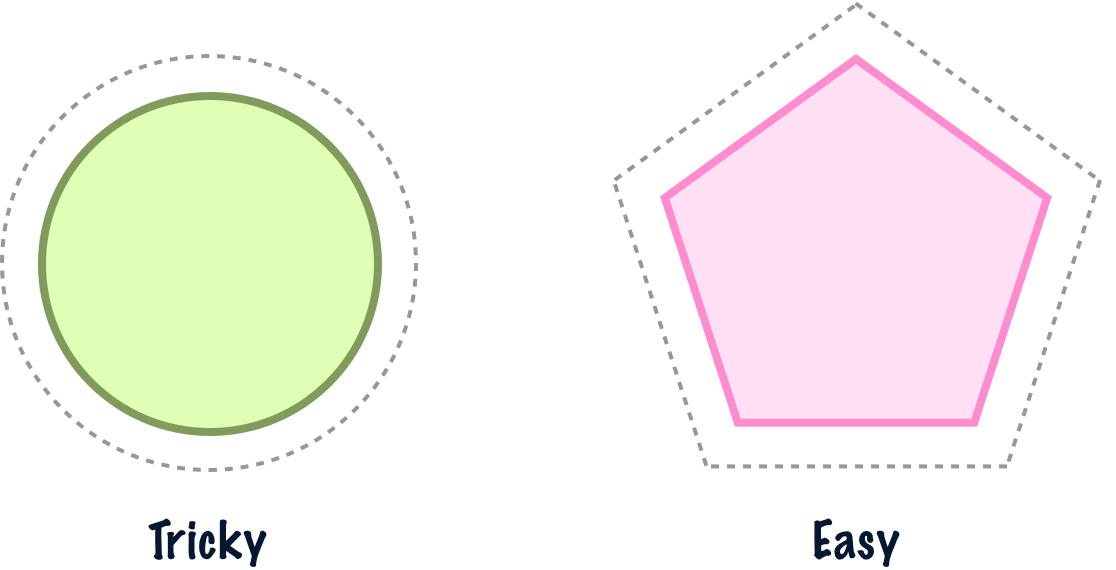
So what Archimedes did was take a circle and wrap it with polygons on the inside and the outside. The outside polygon’s perimeter would be the upper bound of a circle’s circumference. The inner polygon’s perimeter would be the lower bound of a circle’s circumference:
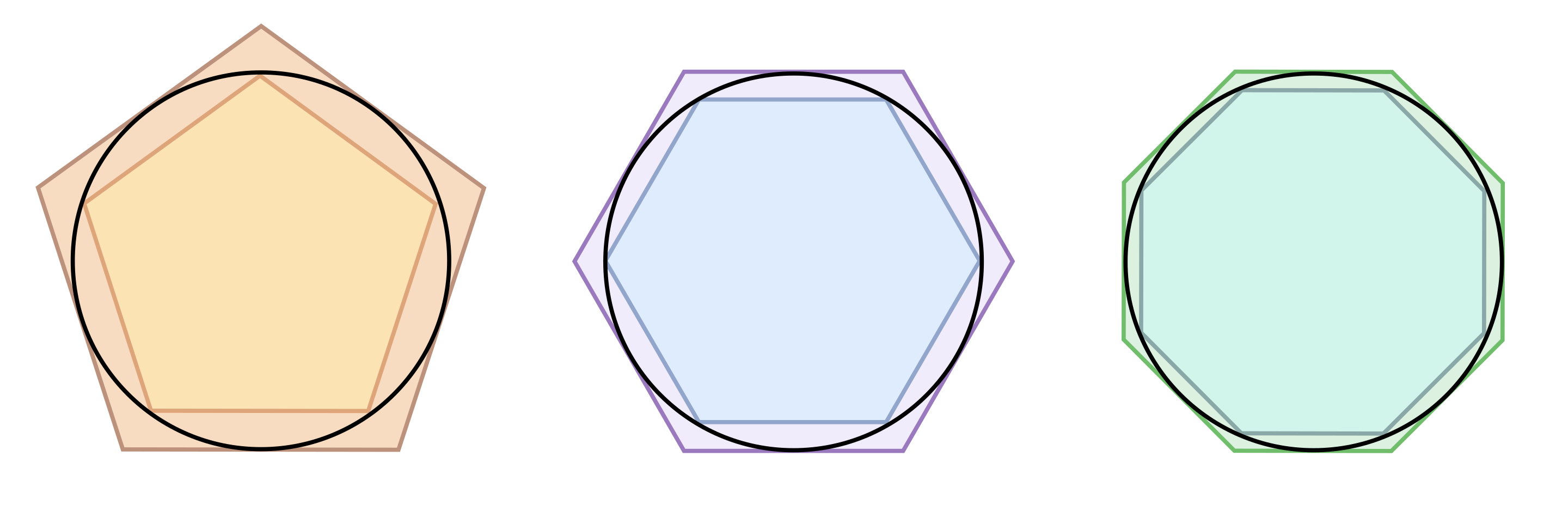
As Archimedes added more sides to the polygons, he was able to more accurately wrap the circle and found that the approximation for pi became more accurate as well. Eventually, a whopping 96 sides later, Archimedes came up with the following range for the value of pi:
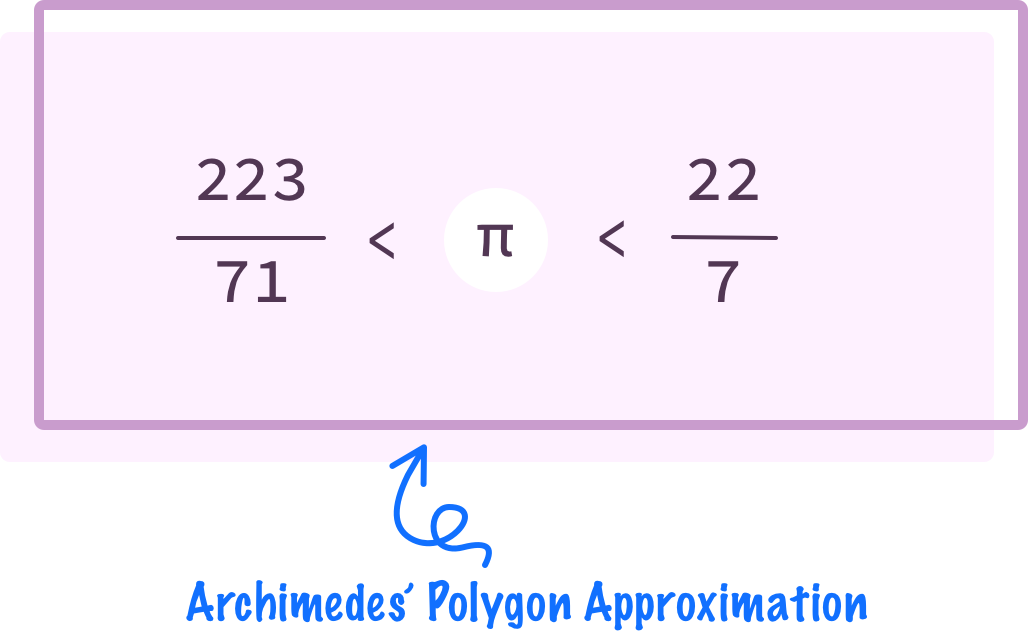
What Archimedes concluded is that the value for pi would fall between 223/71 on the lower end and 22/7 on the upper end. If we turned all of this into JavaScript (with the supporting HTML), what we would see would be something that looks as follows:
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8">
<title>Calculate PI</title>
</head>
<body>
<script>
function calculatePI() {
let lower = 223 / 71;
let upper = 22 / 7;
console.log(lower + ": lower bound!");
console.log(Math.PI + ": value for Math.PI!");
console.log(upper + ": upper bound!");
}
calculatePI();
</script>
</body>
</html>To follow along, create a new HTML file, add the above contents into it, and open this file in the browser. When we bring up our Console, we would see something like the following:
3.140845070422535: lower bound!
3.141592653589793: value for Math.PI!
3.142857142857143: upper bound!We can see how the actual value of Math.PI fits within the range Archimedes calculated. Diving into the specifics of the code we added, our lower and upper calculations for Pi were just divisions of two numbers:
function calculatePI() {
let lower = 223 / 71;
let upper = 22 / 7;
console.log(lower + ": lower bound!");
console.log(Math.PI + ": value for Math.PI!");
console.log(upper + ": upper bound!");
}
calculatePI();This means, for this particular calculation, the only mathematical operator we needed was the / character. This is a good starting point. In the next few sections, we are going to see more advanced techniques for calculating pi that go well beyond division. It’s going to be a hoot...as Archimedes was known to say. I think!
As our understanding of numbers and the various mathematical techniques for working with them grew, we were able to calculate the value of pi really accurately. A key technique from the 16th and 17th centuries that helped here is the application of infinite series techniques towards figuring out pi. What infinite series describe is a way to add an infinite number of items to arrive at a particular finite value, such as pi itself:
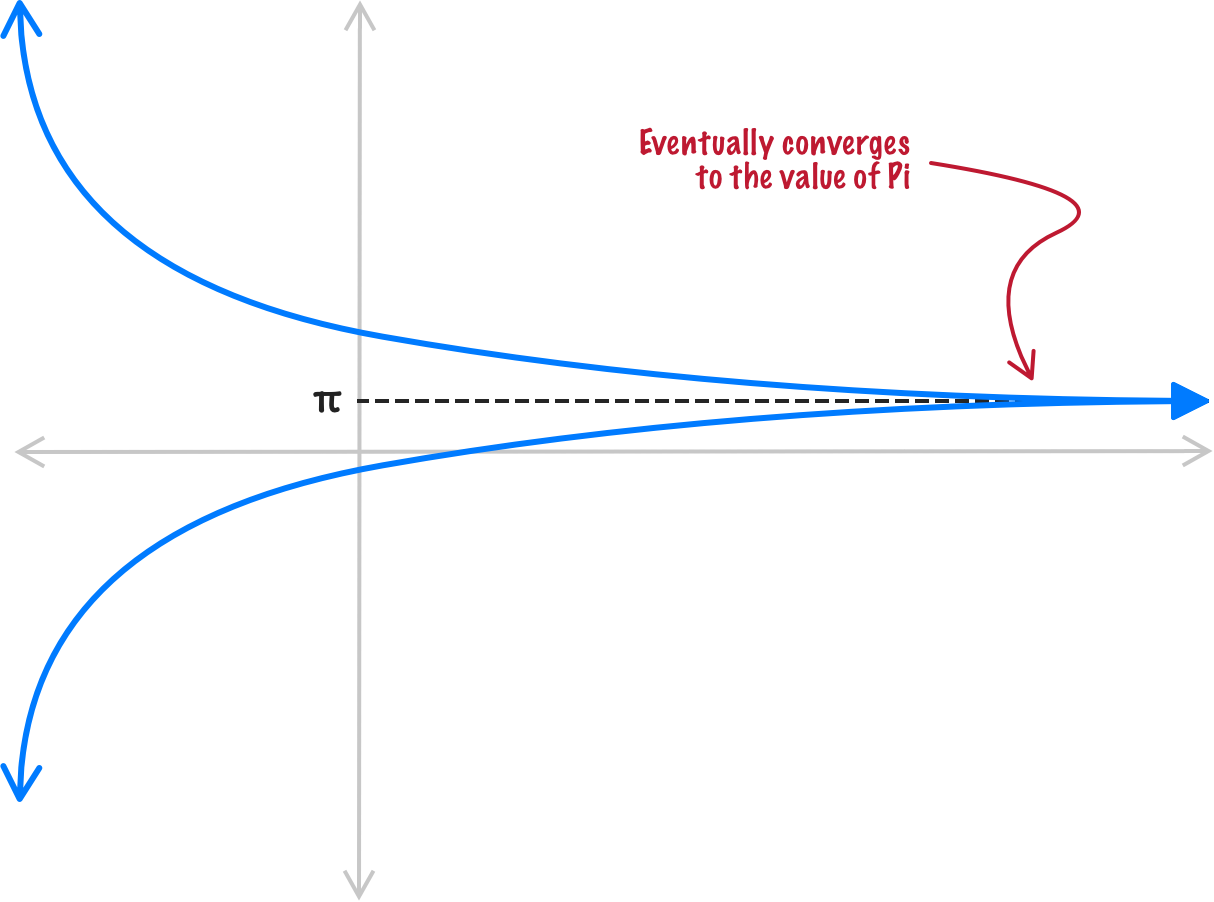
When calculating just a few individual terms of our infinite series, the value we may get may not be very accurate. The more terms we throw into our infinite series calculations, the more accurate the value becomes. The idea is that, as we approach an infinite number of terms that we add up, the number we get at the end is a precise value we are looking for. Let’s look at two implementations of how we can calculate the value for pi by using the infinite series approach.
One infinite series-based approach for calculating PI is the Gregory–Leibniz series, named after Gottried Liebniz and James Gregory. The approach they came up with looks as follows:
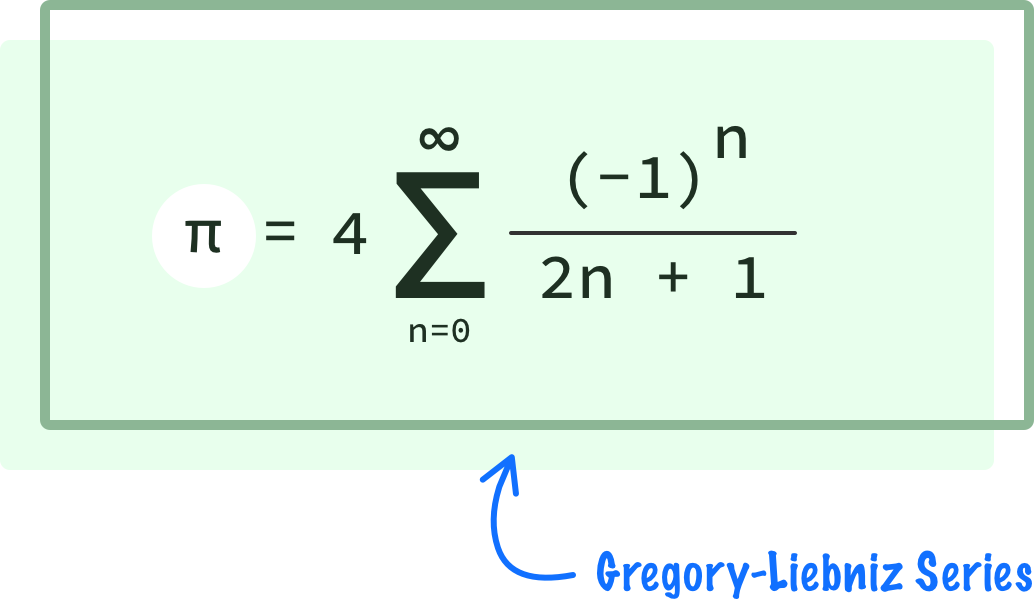
If we had to describe this equation, there are a few parts to it. The biggest part is the sigma character which indicates a sum of multiple terms:
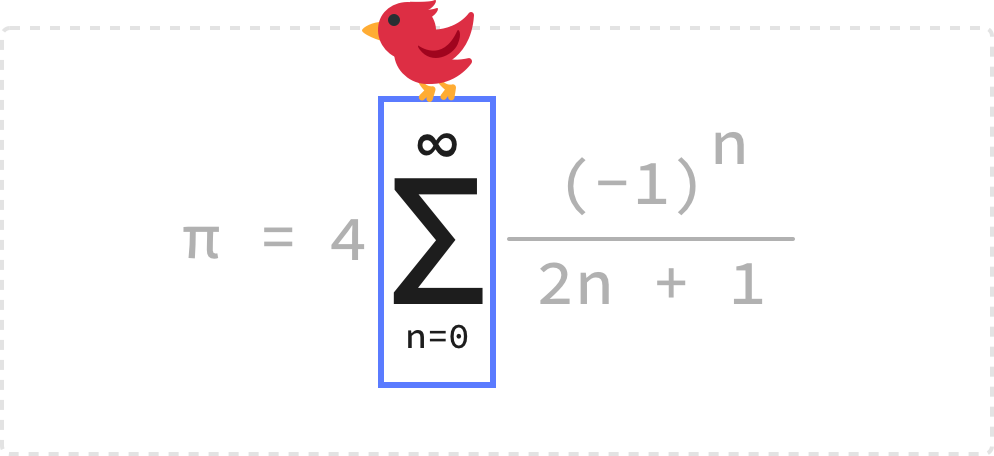
In JavaScript land, think of the sigma character as defining a for loop. The starting condition is n = 0, found at at the bottom of the sigma character. The ending condition is located just above the sigma, and it is set to infinity. This means this equation will run forever (hence the infinite in an infinite series), but we can’t have anything be truly forever in JavaScript. What we’ll do instead is just pick a large number for when our loop will end, such as 1000.
Translating from a mathematical equation to our for loop, we will see something that looks as follows:
for (let n = 0; n < 1000; n++) {
}We mentioned earlier that the sigma character defines a sum of multiple items. What exactly are the items we are summing up? That would be everything after the sigma character:
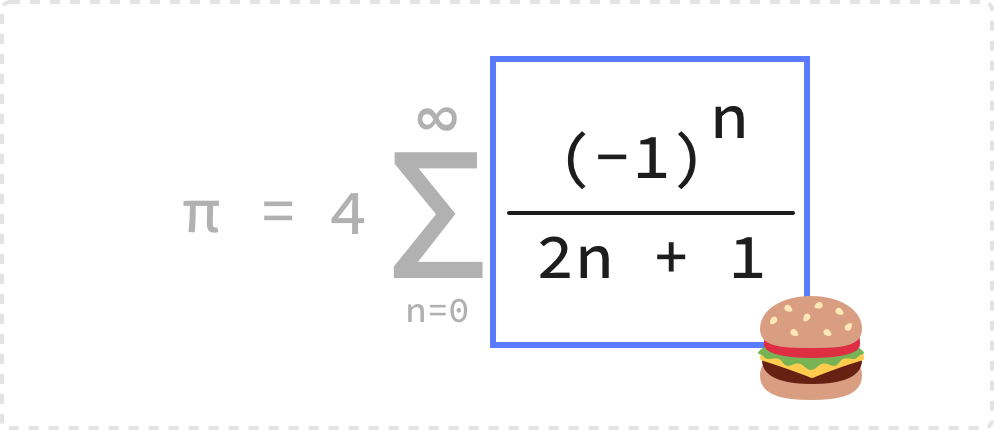
Putting our JavaScript hat back on, the items we are summing up is equivalent to what happens inside our for loop. Turning the rest of our equation into code, what we see will look as follows:
let total = 0;
function calculatePI() {
for (let n = 0; n < 1000; n++) {
let numerator = Math.pow(-1, n);
let denominator = ((2 * n) + 1);
total += (numerator / denominator);
}
}Notice how, for simplicity, we represent the numerator and denominator separately. Critical to making our summation is a variable that stores the result of each iteration, and that is the total variable in our case. We are incrementing the value of total with each run of the loop, and what we are incrementing by is our numerator divided by the denominator:
let total = 0;
function calculatePI() {
for (let n = 0; n < 1000; n++) {
let numerator = Math.pow(-1, n);
let denominator = ((2 * n) + 1);
total += (numerator / denominator);
}
}We are not quite done yet! The last step is to take care of any additional details our mathematical equation may have and calculate the final value. In our case, that is multiplying the results of our summation by 4, so we created a variable called final to help with this:
let total = 0;
let final = 0;
function calculatePI() {
for (let n = 0; n < 1000; n++) {
let numerator = Math.pow(-1, n);
let denominator = ((2 * n) + 1);
total += (numerator / denominator);
}
final = 4 * total;
}
calculatePI();Now that we have our equation translated into JavaScript, we need a way to visualize what our code is doing. Let's add a few console.log statements that, when run, helps us see the value of pi we calculated and the difference between our value and the value returned by Math.PI:
let total = 0;
let final = 0;
function calculatePI() {
for (let n = 0; n < 1000; n++) {
let numerator = Math.pow(-1, n);
let denominator = ((2 * n) + 1);
total += (numerator / denominator);
}
final = 4 * total;
console.log("Value of PI we calculated is: " + final);
console.log("Value of Math.PI is: " + Math.PI);
console.log("Difference is: " + Math.abs(final - Math.PI));
}
calculatePI();When we run our code, this is the output we see for 1000 iterations:
Value of PI we calculated is: 3.140592653839794
Value of Math.PI is: 3.141592653589793
Difference is: 0.000999999749998981The results look a little bit off, right? The 3.14 part looks good, but the rest of the digits don’t seem right. To increase the accuracy of an infinite series calculation, we can increase the number of iterations. In our case, let’s go from 1000 iterations of our loop to 1 million where our loop now has an ending condition of n < 1000000. When we run our code with this increased number of iterations, the output is:
Value of PI we calculated is: 3.1415916535897743
Value of Math.PI is: 3.141592653589793
Difference is: 0.0000010000000187915248Much better, right? If we keep increasing the number of iterations, we will get more accurate results. There is a catch though. The more iterations our code runs, the longer it will take our code to complete. You’ll have to balance speed vs. accuracy, and there is no right answer. It all depends on what you are trying to do. Now, there is another path...a faster and better equation!
As we saw in the previous section, the Gregory-Liebniz series converges to the value of pi very slowly. It took us a lot of iterations (1 million!) to get a reasonably accurate value, but we’d probably need a bunch more iterations to get a “good enough” converged value that rivals Math.PI. Over time, mathematicians continued to find more efficient approaches for calculating pi that converged more quickly and accurately.
One such efficient approach is the BBP Formula, named after its contributors David Bailey, Peter Borwein, and Simon Plouffe. It looks as follows:
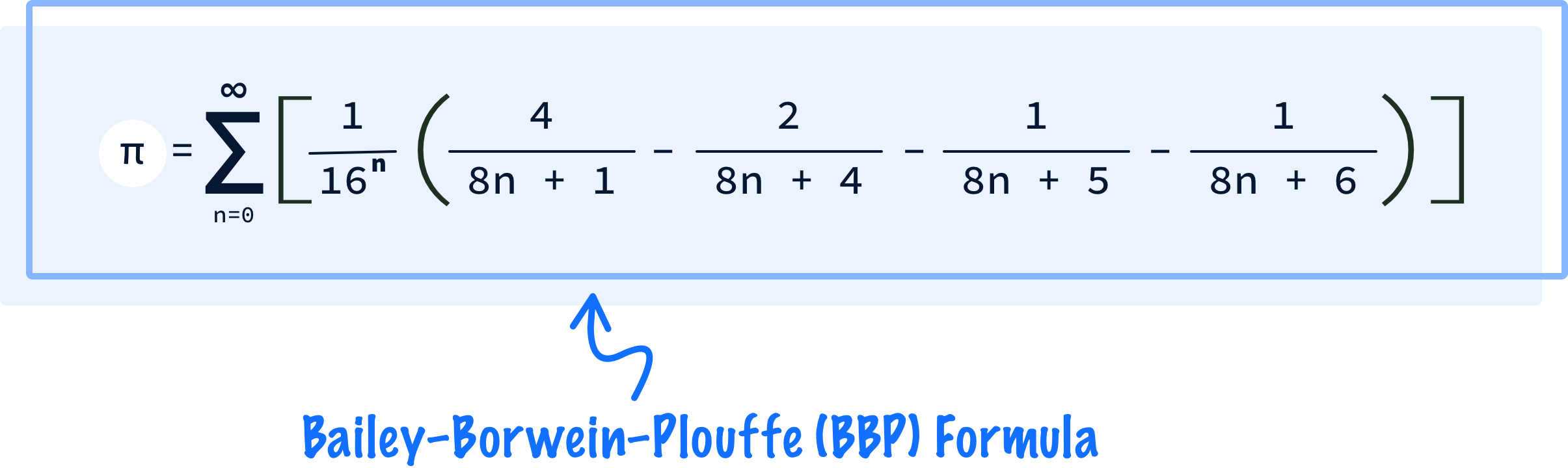
While this mathematical formula seems longer than what we saw earlier, the fundamental techniques we used earlier still hold. There is a sigma operator that defines our looping operation, and there is a bunch of mathematical operations that make up the body of our loop.
If we turned this expression into a JavaScript equivalent, we would get something that looks as follows:
let final = 0;
function calculatePI() {
for (let n = 0; n < 100; n++) {
let scale = (1 / Math.pow(16, n));
let inner = (4 / (8 * n + 1)) - (2 / (8 * n + 4)) - (1 / (8 * n + 5)) - (1 / (8 * n + 6));
let iteration = scale * inner;
final += iteration;
}
console.log("Value of PI we calculated is: " + final);
console.log("Value of Math.PI is: " + Math.PI);
console.log("Difference is: " + Math.abs(final - Math.PI));
}
calculatePI();Take a few moments to understand how we translated our equation into what you see above. In the Gregory-Liebniz series, we broke up our equation into individual numerator and denominator sections. Here we are taking a different path and separating each section based on the parentheses:

There is no right or wrong approach for you to take here. Pick whatever approach you like for turning all of these individual mathematical terms into something we can process in JavaScript.
Before we move on, there is one important detail to call out. Notice that we are running our code for only 100 iterations. Despite the low number of iterations, when we run this code, the output is the following:
Value of PI we calculated is: 3.141592653589793
Value of Math.PI is: 3.141592653589793
Difference is: 0Your eyes don’t deceive you. The output from the BBP approach from just 100 iterations is identical to what we get with our built-in value for Math.PI. Fast and efficient! Who can argue with that?
Now, our quest to more accurately calculate pi didn’t stop with the BBP formula in 1995. Humans are still at it. Because of limitations in how large our numbers in JavaScript can be, there is a limit to how precise we can go in calculating the value for pi. What gets returned for Math.PI is all we need, and we will rarely ever need to calculate the value for Math.PI ourselves outside of fun exercises like what we saw today.
Going beyond JavaScript (yes, there is a beyond!), there are many environments where we need more accurate values for pi. To say there has been exciting work done is an understatement. The latest is the work by Google in calculating Pi to 100 trillion digits:
Yes, that’s a lot of digits of precision. Take a look at their blog post on how they pulled this off and the Chudnovsky algorithm that forms the mathematical basis for the calculation. By the time you read this, there may be even more precise calculations done even faster, so keep your eye out for these things if pi is something you dream about.
Just a final word before we wrap up. What you've seen here is freshly baked content without added preservatives, artificial intelligence, ads, and algorithm-driven doodads. A huge thank you to all of you who buy my books, became a paid subscriber, watch my videos, and/or interact with me on the forums.
Your support keeps this site going! 😇

:: Copyright KIRUPA 2025 //--