Tutorials
Books
Videos
Forums
Table of Contents
It is time for us to learn about the Graph data structure. This particular data structure is used in so many applications and has so much going for it, an entire field of study exists for it called Graph Theory. Smart people every year get advanced degrees in it. There are walls of books dedicated to just this topic. Famous musicians sing songs about...ok, maybe not.
The point to emphasize is that there is a lot to learn when it comes to graphs. We will certainly not cover everything in our time together, but we are going to cover the big topics that we will run into the most in our everyday programming life.
Onwards!
Graphs are a way to organize information and understand how different things are connected to each other. This connected to each other part is important. They help us to find and analyze the relationships between things. Let's start with an example.
Meet Jerry, a fairly successful comedian who lives in New York City:
He has a handful of friends named Elaine, Kramer, and George. We can model Jerry's friendships as follows:
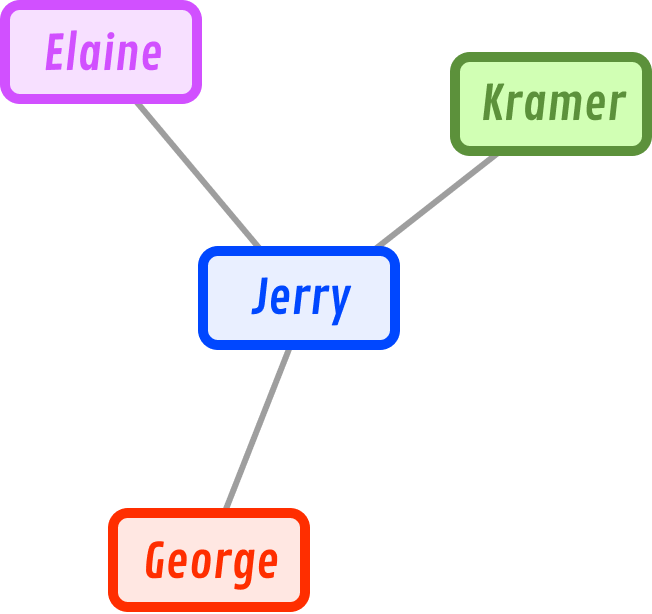
What we have here is a graph. The nodes (also known as vertexes or points) are Jerry, Elaine, Kramer, and George. The connection between the nodes is known as an edge:
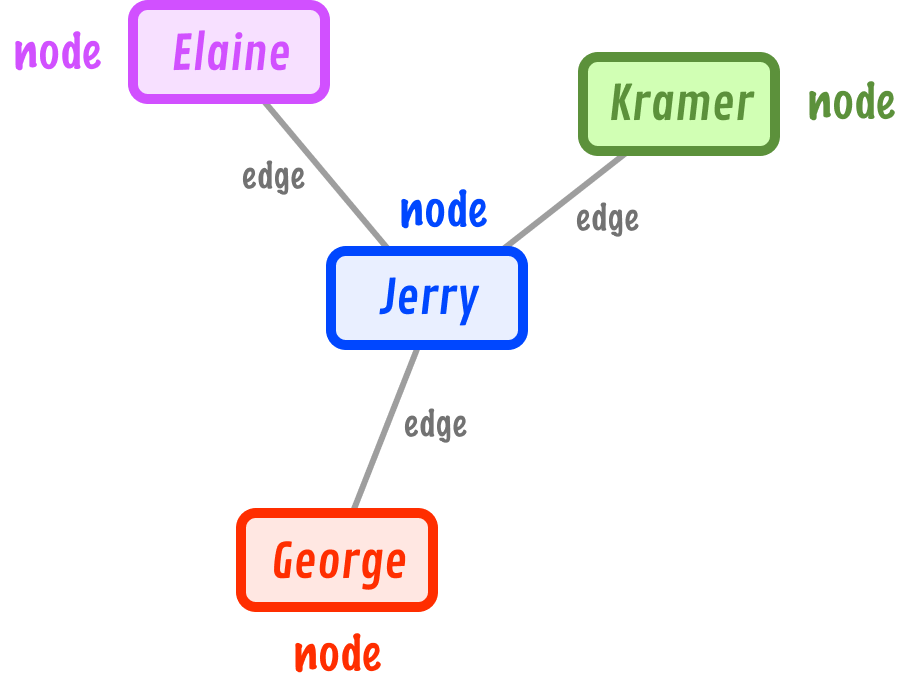
Right now, the edges don't have any direction to them. They are considered to be bi-directional where the relationship between the connected nodes is mutual. A graph made up of only bi-directional edges is known as an undirected graph:
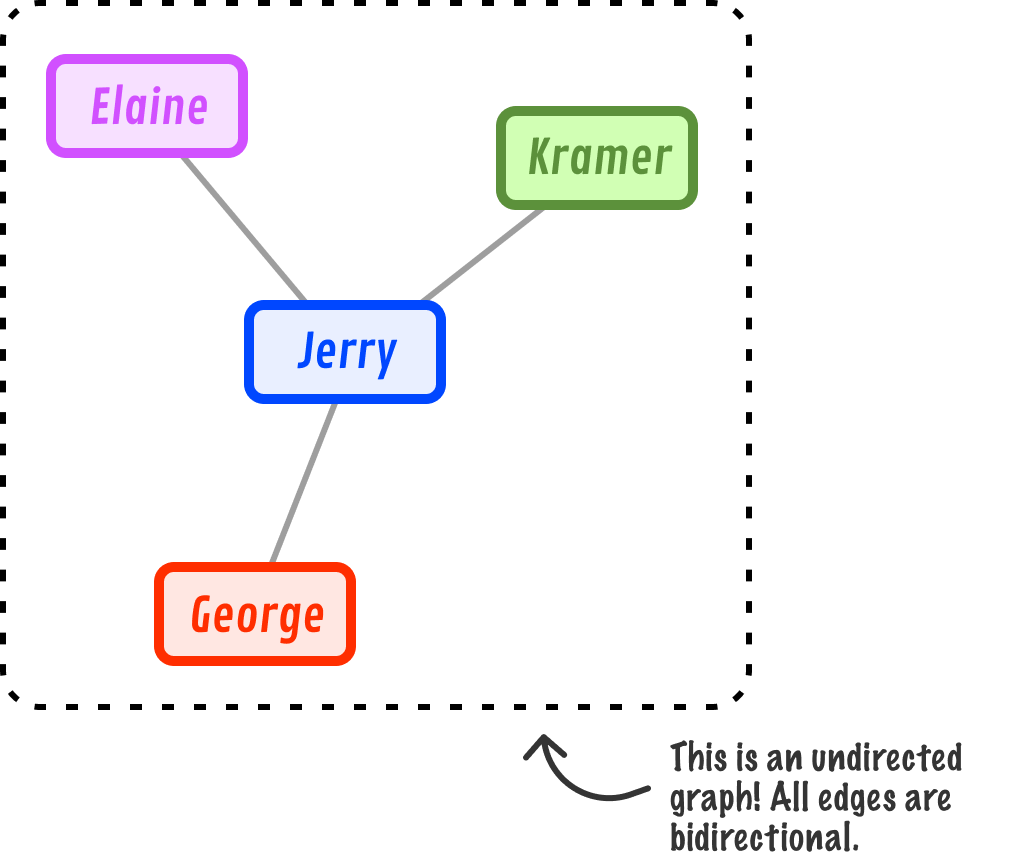
We can also visualize an undirected graph as follows, where the bi-directionalness of the edges is more clearly evident and our ambiguous single path is separated into dedicated paths:
In many real-life cases, our graphs will rarely be undirected. They will have a specific order in the relationship where some connections may be one way. Continuing with our example, Jerry has a friend named Newman. Newman considers Jerry as a friend:
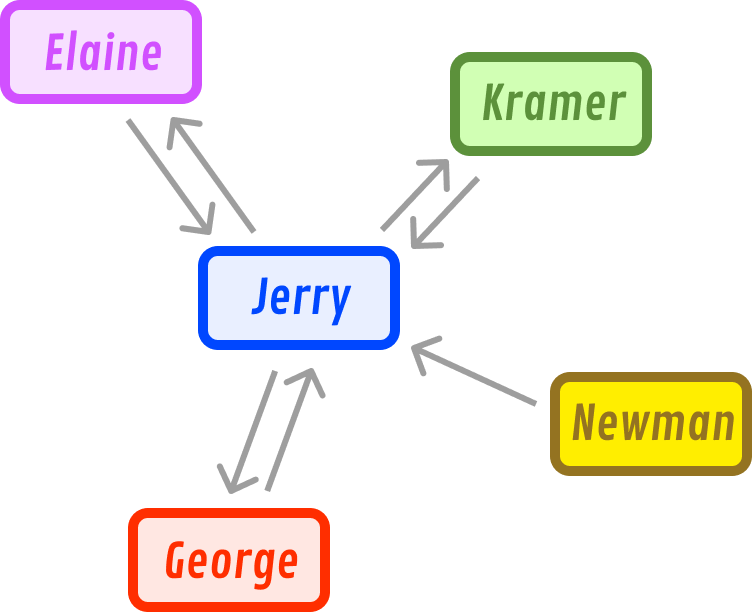
This consideration isn't mutual. Jerry does not consider Newman a friend, so there won't be a reciprocating edge from Jerry pointing towards Newman. A graph where some of the edges have a direction, kind of like what we have right now, is known as a directed graph or digraph for short.
Let's go ahead and detail more of the relationships between Jerry, Elaine, Kramer, George, and Newman:
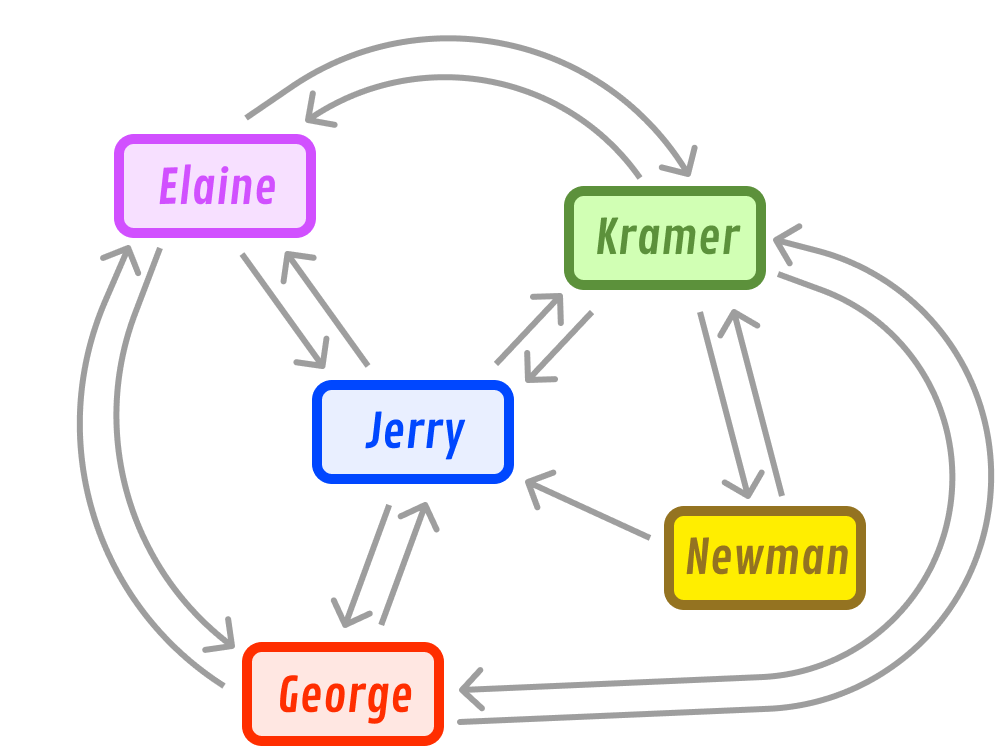
We can now see that Jerry, Elaine, Kramer, and George are mutual friends with each other. Newman is a mutual friend of Kramer, and he has a one-way friendship with Jerry.
There is another detail of graphs that we need to discuss. That has to do with this thing known as cycles. A cycle occurs when we have a path that starts and ends at the same node. For example, our graph highlighting Jerry's friends has many cycles with multiple paths that start and end with each node. If we had to list all the cycles for just Jerry, here are the paths that we can identify:
Graphs with cycles are commonly known as cyclic graphs. We will also encounter graphs that contain no cycles whatsoever:
These graphs are known as acyclic graphs and what we see above is a more specific variation known as a directed acyclic graph (aka dag) because the edges have a direction to them. We also have acyclic graphs that are undirected. Can you guess what these types of graphs are also more commonly known as? Spoiler alert:
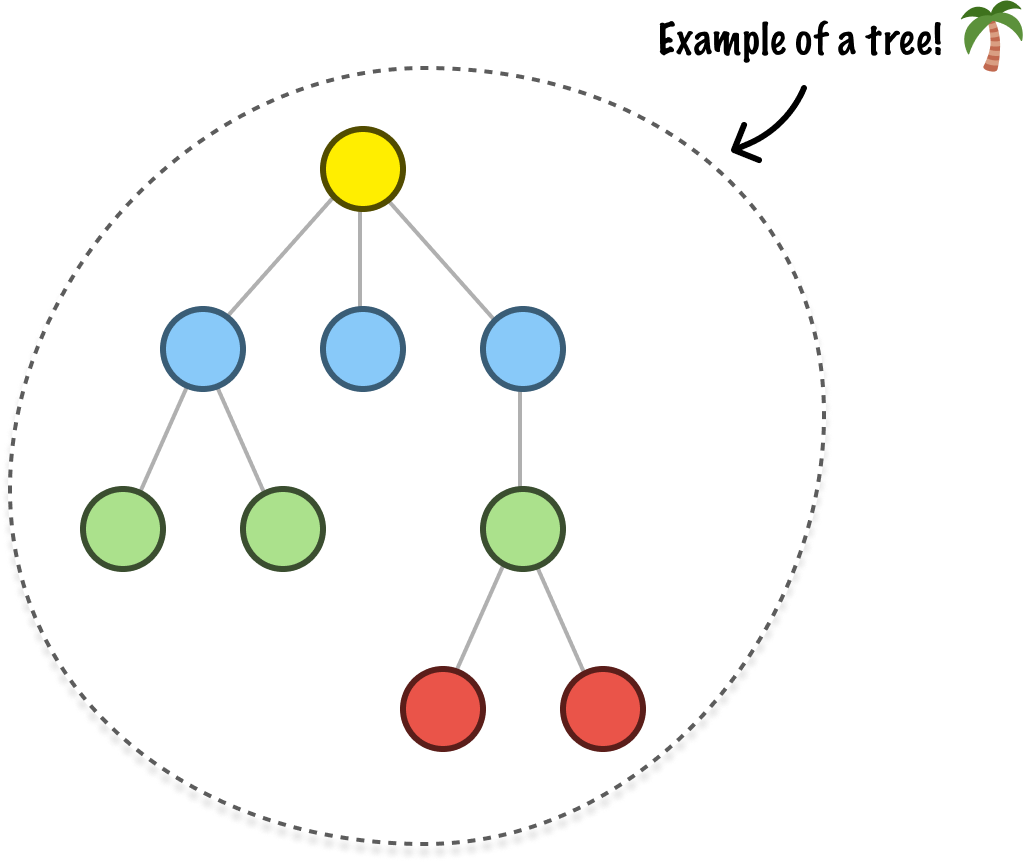
They are known as Trees, a data structure we spent a fair amount of time looking into earlier. Yes, Trees are a very specific type of graph. They are acyclic in that there aren't multiple paths that start from and end at the same node. They are undirected in that the direction of the edges is bidirectional. There is one more detail. The graphs that represent a tree are connected. Connected means that there is a path between every pair of nodes.
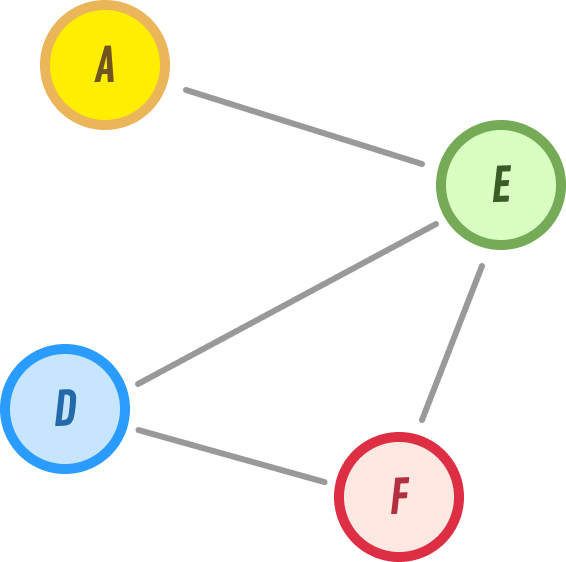
The best way to visualize a connected graph is to look at one that is unconnected:
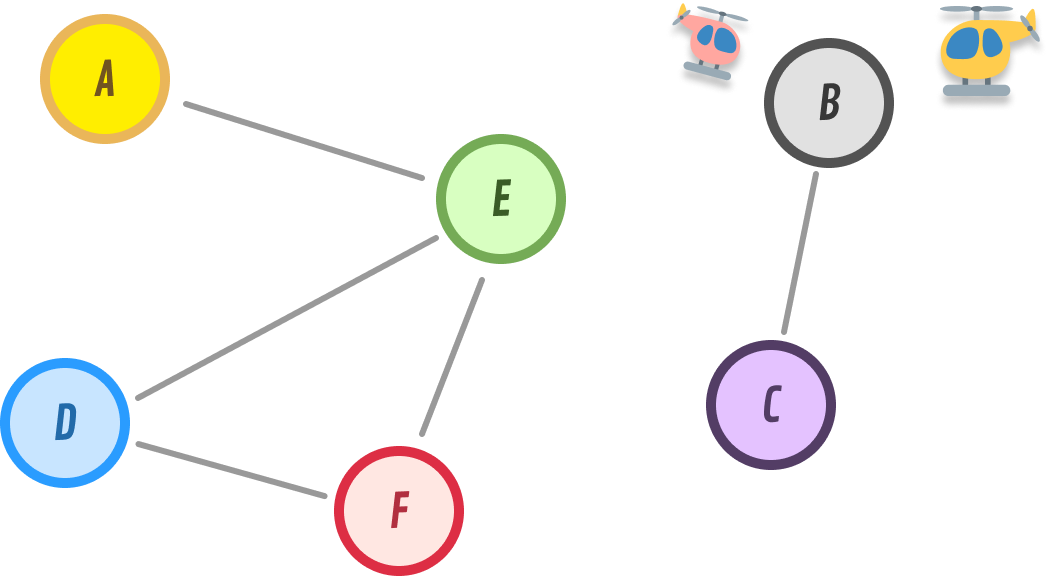
Notice that nodes B and C are floating on an island with no way to get to either B or C from any of the other nodes. For example, is there a path from F to either B or C? The answer is Nope. A connected graph will not have this problem:
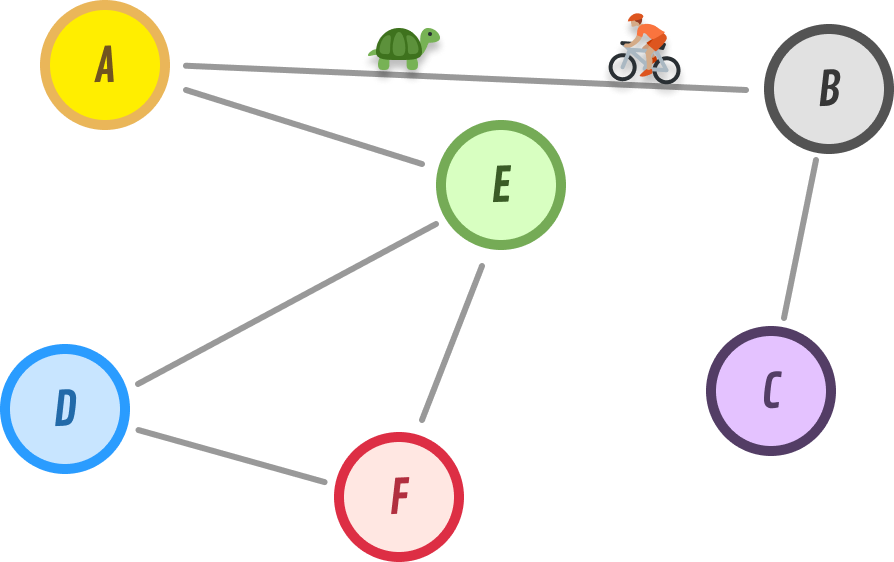
The path created by A and B brings B and C back into connectedness. Now, every pair of nodes in our graph can be reached by some path.
Now that we have a good overview of what graphs are and the variations they come in, it's time to shift gears and look at how we can actually implement one. If we take many steps back, the most common operations we'll do with a graph are:
Before we dive into the implementation, an interesting detail here has to do with how exactly we will represent our node and its relationship with its neighbors. Let's say that we have a graph and a node called A that has the following connections:
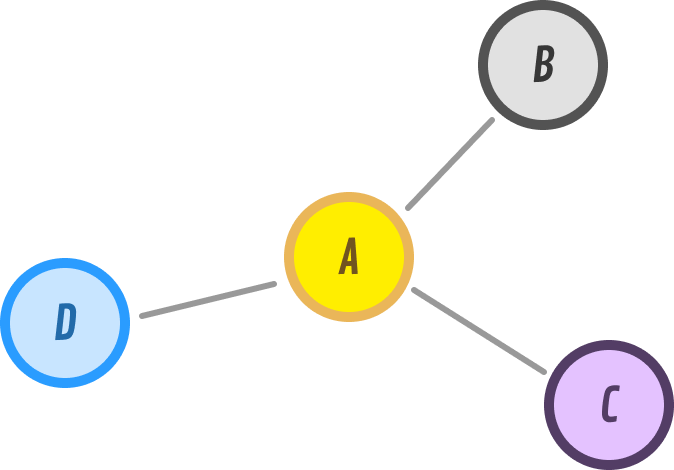
The nodes are A, B, C, and D. We have edges that connect A-B, A-C, and A-D. Because our graph is undirected, the direction of the edges is bidirectional. This means we also have edges that connect B-A, C-A, and D-A.
Getting back to our A node, its neighbors are the nodes B, C, and D. Some nodes will have fewer neighbors, and some nodes can have significantly more. It all boils down to both the type and volume of data our graph represents. So, how would we represent a node's neighbors? One really popular way is by using what is known as an adjacency list.
When using an adjacency list, each node is associated with a list of adjacent nodes. A rough visualization using our current example can look as follows:
A: [B, C, D]
B: [A]
C: [A]
D: [A]This list can take many forms in a potential graph implementation. Our list can be an array, map, hash table, or host of other data structures. Because we mentioned earlier that a node can have a LARGE amount of neighbors, we will want to go with a data structure that makes finding a node lighting fast. This is why, in a few moments, you'll see us representing our adjacency list using a Map (aka Hashtable) data structure.
By using a Map, we can have the key be a node. The value will be a Set data structure whose contents will be all of the neighboring nodes. Sets are great because they don't allow duplicate values. This ensures we avoid a situation where we are going in a loop and adding the same node over and over again.
With the background out of the way, let's dive right in and look at our implementation for the Graph data structure:
class Graph {
constructor() {
// Map to store nodes and their adjacent nodes
this.nodes = new Map();
// Flag to indicate if the graph is directed or undirected
this.isDirected = false;
}
// Add a new node to the graph
addNode(node) {
if (!this.nodes.has(node)) {
this.nodes.set(node, new Set());
}
}
// Add an edge between two nodes
addEdge(node1, node2) {
// Check if the nodes exist
if (!this.nodes.has(node1) || !this.nodes.has(node2)) {
throw new Error('Nodes do not exist in the graph.');
}
// Add edge between node1 and node2
this.nodes.get(node1).add(node2);
// If the graph is undirected, add edge in the opposite direction as well
if (!this.isDirected) {
this.nodes.get(node2).add(node1);
}
}
// Remove a node and all its incident edges from the graph
removeNode(node) {
if (this.nodes.has(node)) {
// Remove the node and its edges from the graph
this.nodes.delete(node);
// Remove any incident edges in other nodes
for (const [node, adjacentNodes] of this.nodes) {
adjacentNodes.delete(node);
}
}
}
// Remove an edge between two nodes
removeEdge(node1, node2) {
if (this.nodes.has(node1) && this.nodes.has(node2)) {
// Remove edge between node1 and node2
this.nodes.get(node1).delete(node2);
// If the graph is undirected, remove edge in the opposite direction as well
if (!this.isDirected) {
this.nodes.get(node2).delete(node1);
}
}
}
// Check if an edge exists between two nodes
hasEdge(node1, node2) {
if (this.nodes.has(node1) && this.nodes.has(node2)) {
return this.nodes.get(node1).has(node2);
}
return false;
}
// Get the adjacent nodes of a given node
getNeighbors(node) {
if (this.nodes.has(node)) {
return Array.from(this.nodes.get(node));
}
return [];
}
// Get all nodes in the graph
getAllNodes() {
return Array.from(this.nodes.keys());
}
// Set the graph as directed
setDirected() {
this.isDirected = true;
}
// Set the graph as undirected
setUndirected() {
this.isDirected = false;
}
// Check if the graph is directed
isGraphDirected() {
return this.isDirected;
}
}Below is an example of how we can use the above graph implementation to perform common graph operations:
// Create a new graph
const characters = new Graph();
characters.setDirected();
// Add nodes
characters.addNode('Jerry');
characters.addNode('Elaine');
characters.addNode('Kramer');
characters.addNode('George');
characters.addNode('Newman');
// Add edges
characters.addEdge('Jerry', 'Elaine');
characters.addEdge('Jerry', 'George');
characters.addEdge('Jerry', 'Kramer');
characters.addEdge('Elaine', 'Jerry');
characters.addEdge('Elaine', 'George');
characters.addEdge('Elaine', 'Kramer');
characters.addEdge('George', 'Elaine');
characters.addEdge('George', 'Jerry');
characters.addEdge('George', 'Kramer');
characters.addEdge('Kramer', 'Elaine');
characters.addEdge('Kramer', 'George');
characters.addEdge('Kramer', 'Jerry');
characters.addEdge('Kramer', 'Newman');
characters.addEdge('Newman', 'Kramer');
characters.addEdge('Newman', 'Jerry');
// Get the adjacent nodes of a node
console.log("Jerry's neighbors: ");
console.log(characters.getNeighbors('Jerry')); // ['Elaine', 'George', 'Kramer']
console.log("Newman's neighbors: ");
console.log(characters.getNeighbors('Newman')); // ['Kramer', 'Jerry']
// Check if an edge exists between two nodes
console.log("Does edge exist between Jerry to Newman? ");
console.log(characters.hasEdge('Jerry', 'Newman')); // false
console.log("Does edge exist between Newman to Jerry? ");
console.log(characters.hasEdge('Jerry', 'Newman')); // true
console.log("Does edge exist between Elaine to George? ");
console.log(characters.hasEdge('Elaine', 'George')); // true
// Get all nodes in the graph
console.log("All the nodes: ");
console.log(characters.getAllNodes()); // ['Jerry', 'Elaine', 'Kramer', 'George', 'Newman']
// Remove a node
console.log("Remove the node, Newman: ")
characters.removeNode("Newman");
console.log(characters.getAllNodes()); // ['Jerry', 'Elaine', 'Kramer', 'George']
console.log("Does edge exist between Kramer to Newman: ");
console.log(characters.hasEdge('Kramer', 'Newman')); // falseTake a moment to walk through the code, especially the comments. As we can see, this implementation of the graph data structure very closely matches the type of graph we have been describing. That's good and bad. It's good because there should be no surprises in our code. It's bad because a more complete graph implementation will contain a few more bells and whistles...which our implementation does not contain. Rest assured that we'll touch upon those missing pieces when we go deeper into looking at graphs in subsequent tutorials.
The graph data structure is one of those fundamental concepts in computer science that you and I can't avoid running into. Because graphs provide a powerful way to model relationships between things, their usefulness is through the roof. So many activities we take for granted such as navigating using an online map, joining a multiplayer game, analyzing data, navigating to anywhere on the internet, and doing a billion other activities all rely on the core capabilities the graph data structure provides. We've only scratched the surface of what graphs are capable of, so there are more graph-related things we are going to cover.
Just a final word before we wrap up. If you have a question and/or want to be part of a friendly, collaborative community of over 220k other developers like yourself, post on the forums for a quick response!
:: Copyright KIRUPA 2024 //--