Linked lists are pretty sweet. They provide an elegant solution for dealing with large amounts of data that are constantly changing, and they have some tricks up their sleeve for doing all of this dealing quickly and efficiently. In this article, we'll explore the ins and outs of linked lists, such as their basic structure, performance characteristics, code implementation, and more! It's going to be a hoot.

Onwards!

Meet the Linked List

Linked lists, just like arrays, are all about helping us store a collection of data. Below we have an example of a linked list we are using to store the letters A through E:

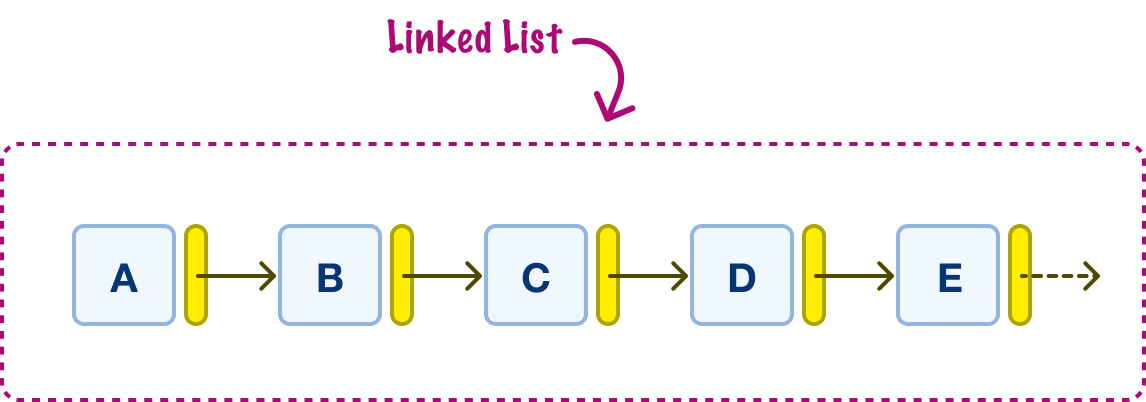
The way linked lists work is by relying on individual nodes that are connected to each other. Each node is responsible for two things:

1. Whatever data it is storing, such as a letter
2. A next pointer (aka reference) that points to the next node in the list

It goes without saying that the node is a big deal. We can zoom in on a node and visualize it as follows:

The abbreviated biography of a linked list is this: when we take a bunch of data, match them with nodes, and connect the nodes together via the next pointer, we have a linked list. How does a linked list become a linked list? How does it help us work with data? Let’s walk through some more details and answer these questions!

Finding a Value

We have a linked list with a bunch of data, and we want to find something. This will be one of the most common operations we’ll perform. The way we do this is by starting with the first node (aka the head node) and traversing through each node as referenced by the next pointer:

We keep jumping from node to node until we either:

1. Find the node whose value we are looking for
2. Reach the last node (aka tail node) that marks the end of our list, and we have nowhere to go

If this sounds a whole lot like a linear search, you would be correct. It totally is...and all the good and bad performance characteristics that it implies.

Adding Nodes

Now, let’s look at how to add nodes to our linked list. The whole idea of adding nodes is less about adding and more about creating a new node and updating a few next pointers. We’ll see this play out as we look at a handful of examples. Let’s say that we want to add a node F at the end:

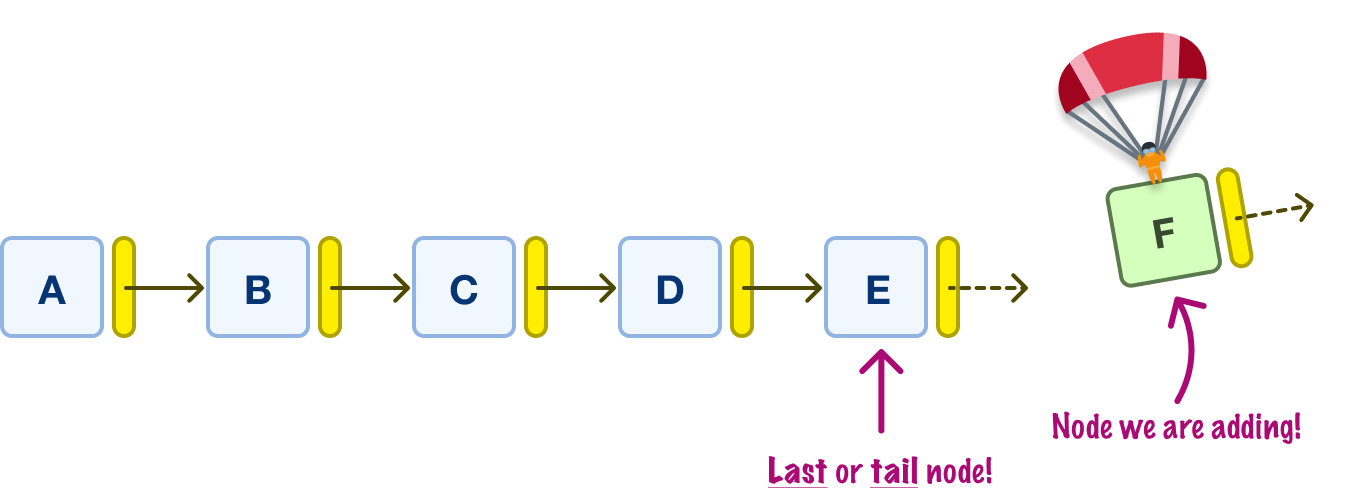
What we need to do is update the next pointer for our tail or last E node to the new node F we are adding:

It doesn’t matter where in our linked list we are adding our new node. The behavior is mostly the same. Let’s say that we want to add a new node Q between our existing nodes of C and D:

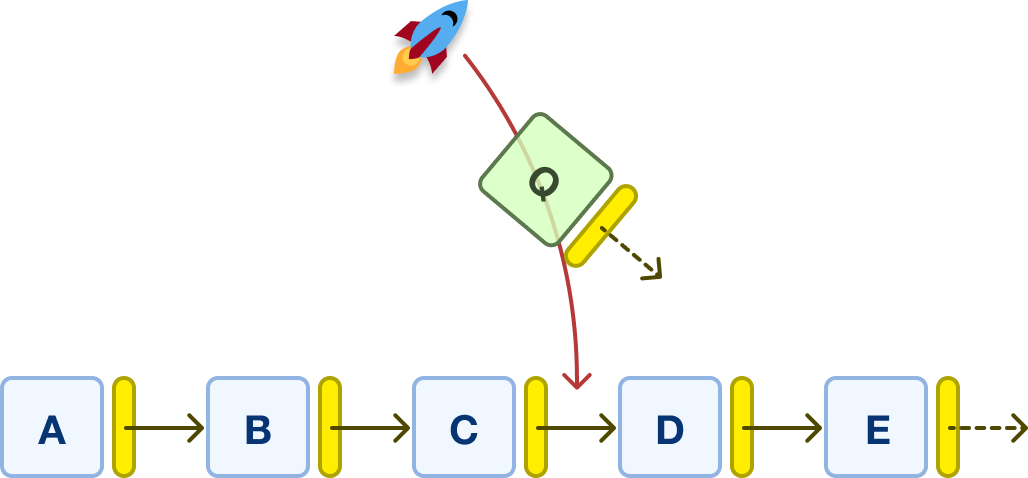
To make this work, the steps we need to take are:

1. Replace the next pointer on C to point to Q
2. Replace the next pointer on Q to point to D

This will result in the following arrangement, which is exactly what we wanted:

An important detail to keep in mind is that it doesn’t matter where in our linked list we are adding our node. Our linked list’s primary job is to ensure the next pointers are updated to account for the newly added node. While this sounds complicated, this is a small amount of work. If we are adding a node to the beginning or end of our linked list, we make only one pointer-related update. If we are adding a node anywhere else but the beginning or end of our linked list, we make two pointer-related updates. That’s pretty efficient!

Deleting a Node

When we want to delete a node, the steps we take are similar-ish to what we did when adding nodes. Let’s say that we want to delete node D in our linked list:

What we do is update the next pointer on node C to reference node E directly, bypassing node D:

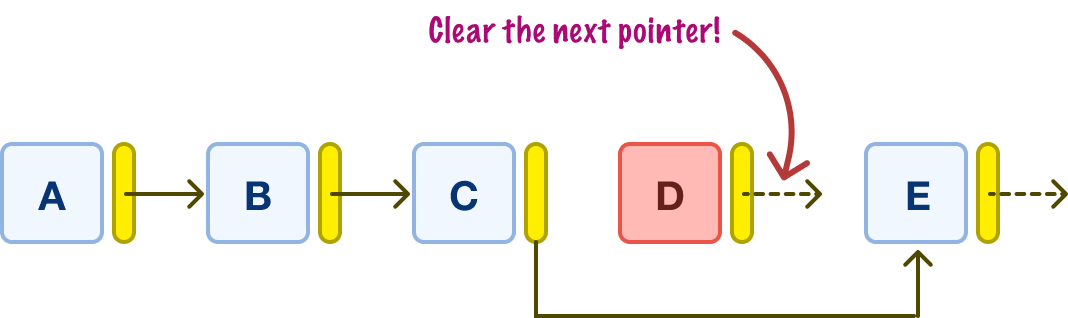
We also clear the next pointer on the D node. All of this makes node D unreachable via a traversal and removes any connection this node has with the rest of the nodes in our linked list. Unreachable does not mean deleted, though. When does node D actually get deleted? The exact moment varies, but this will happen automatically as part of something known as garbage collection when our computer reclaims memory by getting rid of unwanted things.

Linked List: Time and Space Complexity

It’s time for some more fun! We started off our look at linked lists by talking about how fast and efficient they are. For the most common operations, the following table summarizes how our linked list performs:

Action	Best	Average	Worst
Searching	O(1)	O(n)	O(n)
Adding / Insertion	O(1)	O(n)	O(n)
Deleting	O(1)	O(n)	O(n)

An important detail to keep in mind is that the exact implementation of a linked list plays an important role in how fast or slow certain operations are. One implementation choice we will make is that our linked list will have a direct reference to both the first (aka head) node and the last (aka tail) node.

Deeper Look at the Running Time

The table glosses over some subtle (but very important) details, so let's call out the relevant points below:

Search:

• Searching for an element in a singly linked list takes O(n) time. This is because we have to traverse the list from the beginning to find the element
• If what we are looking for happens to be the first item, then we return the found node in O(1) time

Adding / Insertion:

• Inserting an element at the beginning or end of a singly linked list takes O(1) time, as we only need to update the reference of the new node to point to the current head or tail of the list.
• Inserting an element at a specific position in the list takes O(n) time in the average and worst cases, for we have to traverse through the list to find the position

Deletion:

• Similar to the adding case, deleting an element from the beginning or end of a singly linked list takes O(1) time, as we only need to update the reference of the first or last node.
• Deleting an element from a specific position in the list takes O(n) time in the average and worst cases, for we have to traverse the list to find the element and then delete it

Space Complexity

From a memory/space point of view, linked lists require O(n) space. For each piece of data we want our linked list to store, we wrap that data into a node. The node itself is a very lightweight structure where all it contains is a thin wrapper to store our data and a reference to the next node.

Linked List Variations

As it turns out, linked lists aren't a one-size-fits-all phenomenon. We'll want to be aware of a few popular variations and talk through what makes them useful.

Singly Linked List

The singly linked list, spoiler alert, is the type of linked list we have been looking at in-depth so far:

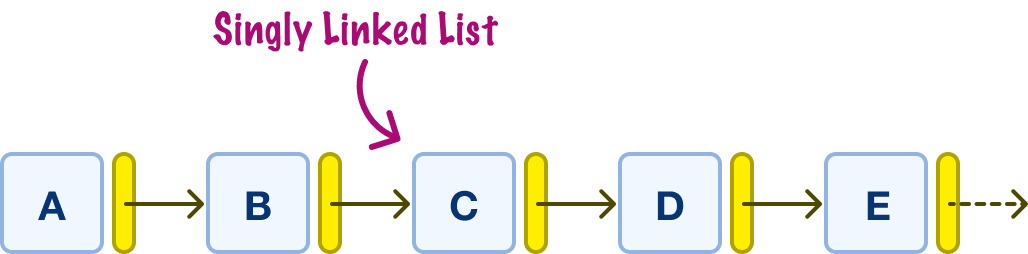
In a singly linked list, each node has exactly one pointer that references the next node. For many situations, this one-way behavior is perfectly adequate.

Doubly Linked List

In a doubly linked list, each node has two pointers, one to the previous node and one to the next node:

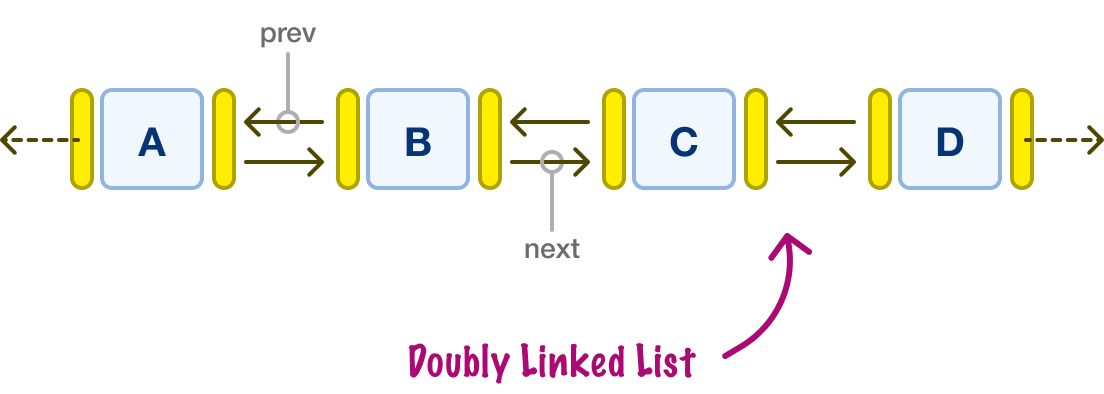
This allows for easier traversal in both directions, similar to moving from a one-lane road to a two-lane one. We'll typically see a doubly linked list being used in implementations of associative arrays and other complex data structures.

Circular Linked List

In a circular linked list, the last node's next pointer points to the first node, creating a circular structure:

This can be used in situations where items need to be accessed in a circular fashion, such as a scheduling algorithm, picking the next player in a game of poker, and more. Speaking of poker:

Sorry. I couldn't resist. If you mention poker, I am obligated to share this image.

Skip List

We already saw that linked lists are fast. Skip lists make things even faster. A skip list is a linked list that includes additional "skip" links that act like shortcuts to make jumping to points in the list faster:

Notice that each level of our skip list gives us faster access to certain elements. Depending on what data we are looking for, we will be traversing both horizontally as well as up and down each level to minimize the number of nodes we need to examine.

Skip lists are often used in situations where we need to perform frequent lookups or searches on a large dataset. By adding skip links to a linked list, we can reduce the amount of time it takes to find a specific element while still maintaining the benefits of a linked list (such as constant time insertion and deletion).

Implementation

With our linked list, there are a handful of operations that are going to be critical for us to support. Those operations will be:

• Creating a new linked list
• Adding item at the beginning
• Adding item at the end
• Adding an item before an existing item
• Adding an item after an existing item
• Checking if our linked list contains a specific item
• Removing the first item
• Removing the last item
• Removing a specific item
• Converting our items into an array
• Getting the length of our linked list

Here is our implementation that supports all of these operations we have listed:

class LinkedListNode {
  constructor(data, next = null) {
    this.data = data;
    this.next = next;
  }
}

class LinkedList {
  constructor() {
    this.head = null;
    this.tail = null;
    this.size = 0;
  }

  addFirst(data) {
    const newNode = new LinkedListNode(data, this.head);

    this.head = newNode;

    if (!this.tail) {
      this.tail = newNode;
    }

    this.size++;
  }

  addLast(data) {
    const newNode = new LinkedListNode(data);

    if (!this.head) {
      this.head = newNode;
      this.tail = newNode;
    } else {
      this.tail.next = newNode;
      this.tail = newNode;
    }

    this.size++;
  }

  addBefore(beforeData, data) {
    const newNode = new LinkedListNode(data);

    if (this.size === 0) {
      this.head = newNode;
      this.size++;
      return;
    }

    if (this.head.data === beforeData) {
      newNode.next = this.head;
      this.head = newNode;
      this.size++;
      return;
    }

    let current = this.head.next;
    let prev = this.head;

    while (current) {
      if (current.data === beforeData) {
        newNode.next = current;
        prev.next = newNode;
        this.size++;
        return;
      }

      prev = current;
      current = current.next;
    }

    throw new Error(`Node with data '${beforeData}' not found in list`);
  }

  addAfter(afterData, data) {
    const newNode = new LinkedListNode(data);

    if (this.size === 0) {
      this.head = newNode;
      this.size++;
      return;
    }

    let current = this.head;

    while (current) {
      if (current.data === afterData) {
        newNode.next = current.next;
        current.next = newNode;
        this.size++;
        return;
      }

      current = current.next;
    }

    throw new Error(`Node with data '${afterData}' not found in list!`);
  }

  contains(data) {
    let current = this.head;

    while (current) {
      if (current.data === data) {
        return true;
      }

      current = current.next;
    }

    return false;
  }

  removeFirst() {
    if (!this.head) {
      throw new Error('List is empty');
    }

    this.head = this.head.next;
    if (!this.head) {
      this.tail = null;
    }
    this.size--;
  }

  removeLast() {
    if (!this.tail) {
      throw new Error('List is empty');
    }

    if (this.head === this.tail) {
      this.head = null;
      this.tail = null;
      this.size--;
      return;
    }

    let current = this.head;
    let prev = null;

    while (current.next) {
      prev = current;
      current = current.next;
    }

    prev.next = null;
    this.tail = prev;
    this.size--;
  }

  remove(data) {
    if (this.size === 0) {
      throw new Error("List is empty");
    }

    if (this.head.data === data) {
      this.head = this.head.next;
      this.size--;
      return;
    }

    let current = this.head;

    while (current.next) {
      if (current.next.data === data) {
        current.next = current.next.next;
        this.size--;
        return;
      }

      current = current.next;
    }

    throw new Error(`Node with data '${data}' not found in list!`);
  }

  toArray() {
    const arr = [];

    let current = this.head;

    while (current) {
      arr.push(current.data);
      current = current.next;
    }

    return arr;
  }

  get length() {
    return this.size;
  }
}

To see this code in action, here are some example prompts:

let letters = new LinkedList();
letters.addLast("A");
letters.addLast("B");
letters.addLast("C");
letters.addLast("D");
letters.addLast("E");

console.log(letters.toArray()); // ['A', 'B', 'C', 'D', 'E']

letters.addFirst("AA");
letters.addLast("Z");

console.log(letters.toArray()); // ['AA', 'A', 'B', 'C', 'D', 'E', 'Z']

letters.remove("C");
letters.removeFirst();
letters.removeLast();

console.log(letters.toArray()); // ['A', 'B', 'D', 'E']

letters.addAfter("D", "Q");

console.log(letters.toArray()); // ['A', 'B', 'D', 'Q', 'E']

letters.addAfter("Q", "H");
letters.addBefore("A", "5");

console.log(letters.toArray()); // ['5', 'A', 'B', 'D', 'Q', 'H', 'E']

console.log(letters.length); // 7

To see a live example of all the code you see above, visit this Codepen demo. In the future, if we need to use this LinkedList in our code, we can either copy/paste all of this code or reference it directly by adding the following script tag:

<script src="https://www.kirupa.com/js/linkedlist_v1.js"></script>

As we'll see shortly, the linked list plays a crucial role in how several other data structures and algorithms are implemented.

Conclusion

Phew! As we saw across the many words and diagrams, linked lists provide an efficient way to store and manipulate data. They allow for constant time insertion and deletion, and they can be easily traversed to perform operations such as searching. While they aren't the most efficient data structure out there, they can safely claim the top spot in their simplicity. As we will see in the next article, building a linked list in JavaScript is just as elegant as our explanation of how they work.

Just a final word before we wrap up. If you have a question and/or want to be part of a friendly, collaborative community of over 220k other developers like yourself, post on the forums for a quick response!