Search Algorithms and Linear Search

by kirupa   |   filed under Data Structures and Algorithms

In the real world, when we talk about search or searching, we are trying find something. What we are trying to find could be a sock in a pile of clothes, a needle in a haystack, a matching fork to go with a knife, Waldo (and possibly his dog companion Woof), car keys, a particular star in our solar system, and a billion other things:

In our algorithmic digital world, when we talk about search or searching, we are still trying to find something. The key difference is that what we are trying to find will live in a collection of data, such as an array, a list, or a tree. Depending on what we are looking for and what the collection of data looks like, we will employ a variety of approaches to help us find something efficiently. These varieties of approaches have a more formal name. They are known as search algorithms.

Together, we're going to look at some really popular search algorithms, each with their own unique twist that makes them special. In this tutorial, we are going to start our journey by looking at one of the most approachable search algorithms, the linear search (sometimes also referred to as a sequential search).

Onwards!

For a comprehensive and beginner-friendly look at data structures and algorithms, check out Kirupa's best-selling book on this topic.

BUY ON AMAZON

Linear Search

As search algorithms go, linear search is easy to explain. It works by iterating through each item in a collection of data and checking if the item you are on matches the item you are looking for. This search will continue until either we find the item or we reach the end of our collection and ended up not finding the item. Let's look at an example.

Linear Search at Work

Here is our setup. We have a collection of items stored in an array:

What we want to do is find the item whose value is 3:

With linear search, we start at the beginning with the first item (aka array index position 0) and ask ourselves this question: Is the value at this location the same as what I am looking for? For our example, we check if our first item 5 is the same as 3...which we know isn't the case:

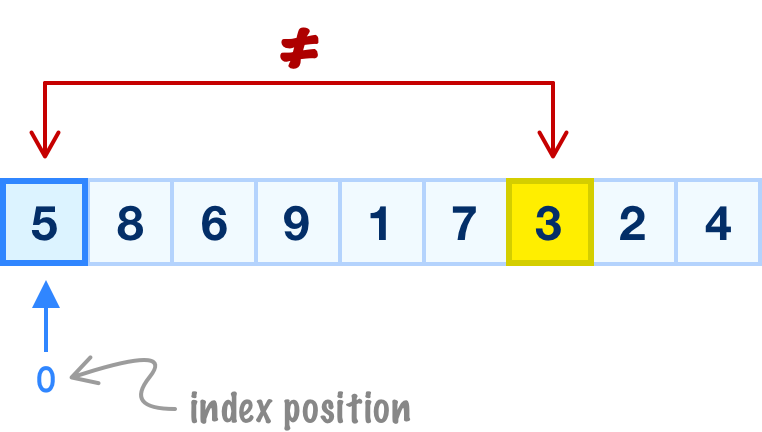
Because we don't have a match, we move to the next item in our array and repeat the same process. We ask if the value at this location the same as what I am looking for? We know that our second item's value is 8, and 8 isn't equal to 3 either:

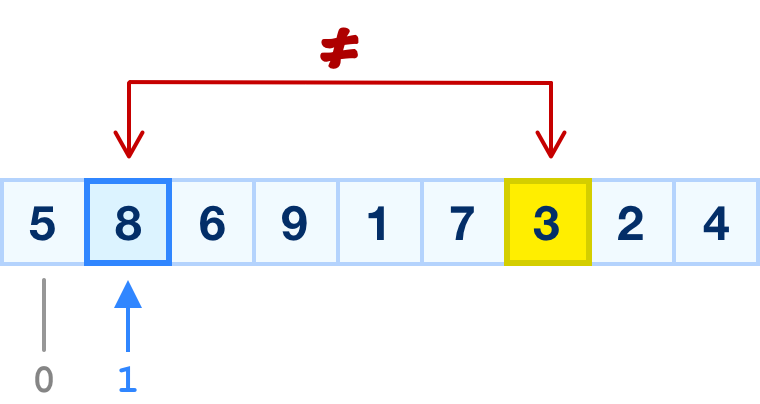
This pattern keeps repeating. We keep going down each item in our array until we eventually get to the item storing our 3 value:

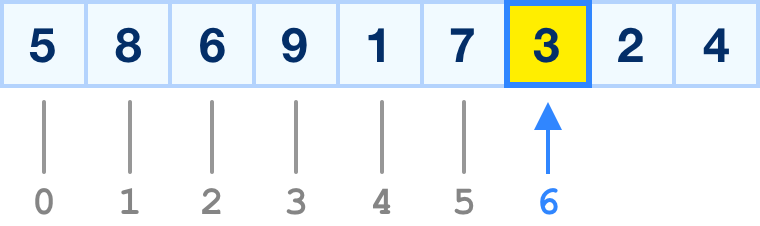
At this point, we have a match. We found what we were looking, and it was at array index position 6.

If our array never contained the item we are looking for, we would have examined every item in our array and returned the equivalent of a "Not found" result upon reaching our last item.

JavaScript Implementation

If we turn all of our words and diagrams into code, below is what one implementation of our linear search algorithm can look like:

function linear_search(collection, item) {
  for (let i = 0; i < collection.length; i++) {
    if (collection[i] === item) {
      // Return index position of found item
      return i;
    }
  }
  // Item not found
  return -1;
}

We have a function called linear_search, and it takes two arguments. The first argument is our array, and the second argument is for the item we are looking for. If the item we are looking for is found, our code will return the index position of the found item:

let data = [5, 8, 6, 9, 1, 7, 3, 2, 4];

let result = linear_search(data, 3);
console.log(result) // 6

If the item we are looking for is not found, our code will return return a -1:

let data = [5, 8, 6, 9, 1, 7, 3, 2, 4];

let result = linear_search(data, "koala");
console.log(result) // -1

The -1 answer is a popular convention in JavaScript and other programming languages for signaling that something we are looking for can't be found. You are certainly welcome to change it to something else like the string Not found if that is more to your liking.

Runtime Characteristics

Our linear search algorithm runs in O(n) linear time. The best case scenario is when the item we are looking for happens to be the first item in our collection of data. In this case, we can just stop after reaching the first item. The worst case scenario happens in one of two cases:

1. The item we are looking for happens to be in the last spot in our colletion of data
2. The item we are looking for doesn't existing in our collection of data at all

In both of these cases, we had to go and examine every item in our array until we reached the end. The number of operations this takes is directly related to the number of items in our collection. There are no shortcuts here. If we have a bunch of items, our linear search will start at the beginning and go through each item to find what we are looking for.

function global_linear_search(collection, item) {
  let foundPositions = [];

  for (let i = 0; i < collection.length; i++) {
    if (collection[i] === item) {
      // Store position of found item
      foundPositions.push(i);
    }
  }

  if (foundPositions.length > 0) {
    return foundPositions;
  } else {
    // No items found
    return -1;
  }
}

let data = [5, 8, 3, 9, 1, 7, 3, 2, 4, 3, 6];

let result = global_linear_search(data, 3);
console.log(result) // [2, 6, 9];

Conclusion

Hopefully, we can see that the linear search algorithm is a simple and straightforward approach for finding an item within a collection of data. Because we iterate through each item in our collection, linear search isn't considered to be a fast algorithm. It is quite inefficient for large collections of data. This doesn't mean that we won't ever have a practical use for it, though. Linear search is useful in situations where our collection of data is small, our data is unsorted, or the item we are looking for is going to be stashed somewhere towards the beginning of our collection.

Just a final word before we wrap up. If you have a question and/or want to be part of a friendly, collaborative community of over 220k other developers like yourself, post on the forums for a quick response!