Tutorials
Books
Videos
Forums
Table of Contents
Bubble sort is a simple sorting algorithm that repeatedly steps through a list, compares adjacent elements, and swaps them if they are in the wrong order. Learn all about what makes it tick and why we probably don't want to use it for larger datasets.
When it comes to sorting stuff, one of the worst algorithms you can use is known affectionately as bubble sort. It is sooo terrible, that people have stopped naming kids after it. It's like the Bart of the algorithms world:
Despite its terribleness, bubble sort is a foundational sorting algorithm that helps us to better understand yet-another-way one can sort data using an inefficient approach.
By learning how bubble sort works, you can use this knowledge to avoid doing anything in your code that even remotely resembles it.
Onwards!
If we had to TL;DR how bubble sort works, it would be as follows: bubble sort repeatedly steps through a list, compares adjacent elements, and swaps them if they are in the wrong order. Seems simple enough, so let's walk through in more detail what all of that means.
For our starting point, we have a collection of numbers that are currently unsorted:
The way bubble sort works involves a lot of comparisons. In the beginning, it starts by comparing the first item with the second item:
If the first item is smaller than the second item, then it moves on to the next pair of numbers. In our case, the first item (6) is not smaller than the second item (2). The second item is larger, so we do a swap between these two numbers to ensure the first item is smaller than the second item:
At this point, we are done with our first two numbers...for now. Next, we move to the next pair of adjacent numbers starting with the second item and do our comparison check between these two numbers:
When we examine these two numbers, the first item is 6. The second item is 0. The first item is not less than the second item, so we swap these two values:
Can you guess what we do next? If you guessed that we would shift over to the next two numbers to perform a comparison, you would be right!
The next two numbers we compare will be be the 6 and the 9:
Is the first value (6) less than the second number (9)? It certainly is! This means we don't need to do a swap:
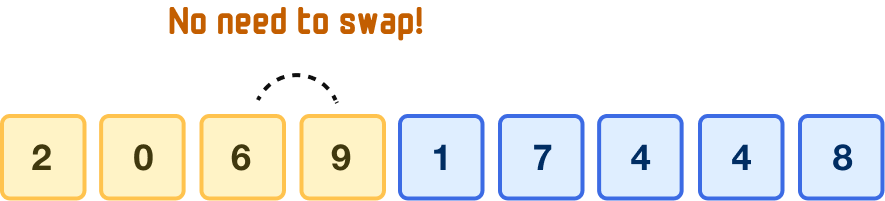
The relative order of both of these numbers is correct where the first number is smaller than the second number, so we leave them alone.
As you can probably surmise, we repeat this process of sliding over by one, comparing the two numbers in front of us, swapping them if we need to, and repeating all of this until we have no more numbers left when we reach the end of our list:
When we reach the last number, do we have a sorted collection of values? The answer is a resounding No, for we have many numbers out of place. What happens next is that we start back at the beginning of our collection and repeat all of these steps over and over again until all of our numbers are sorted.
When do we know when all of our numbers are sorted? We know our numbers are sorted when we go through our collection without having to do any swapping operation at any point. That's when we know that every number is in the correct place and sorted from smallest to largest:
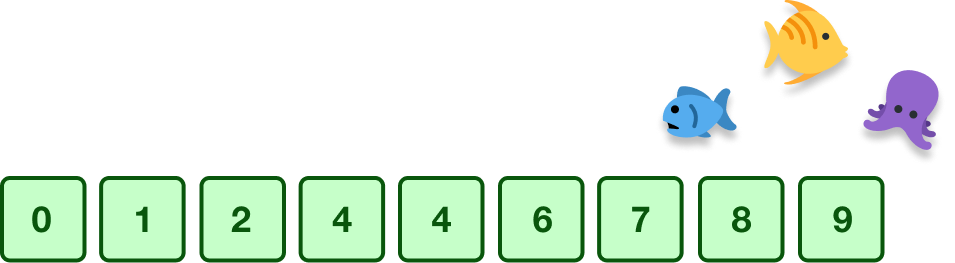
We will talk about this later, but sorting these values using bubble sort won't be done quickly. There will be a lot of steps where we compare, swap, and repeat.
Each time we go through our unsorted collection, the largest unsorted number will get caught up in the swapping behavior at each step and get carried all the way (aka bubbled up) to the correct spot in the end. In our above example, the largest number is 9. Once we encounter it for the first time, we keep swapping it until it is placed at the last spot:
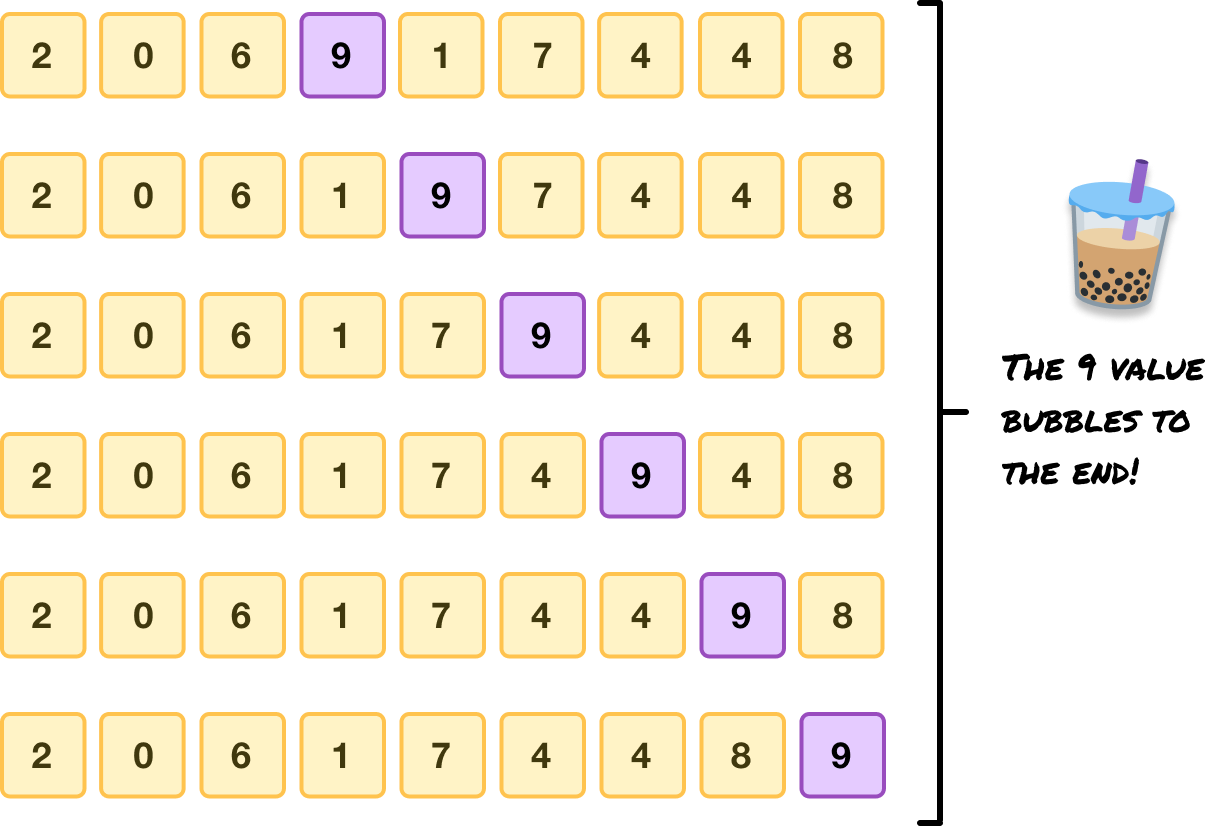
The next time we run through our collection, the next highest number (which is the 8) will ultimately find itself caught in this same bubbling behavior and end up in its final sorted position just before the 9. This behavior should help explain why this sorting algorithm is called bubble sort. It is certainly not for its bubbly personality.
Also, we may sometimes see bubble sort sometimes be referred to as sinking sort where the bubbling behavior could also be interpreted as a sinking behavior instead.
In the previous section, we learned a bit at a high-level about how bubblesort works. In this section, let's fully clarify everything we've seen so far by doing a full walkthrough. To avoid boring you to tears, I'm going to pick an example that only has four numbers.
Don't worry. Since we are dealing with bubblesort, these four numbers itself will ensure you and I do a lot of scrolling (or page turning or hand gesturing) to get to the fully sorted version of things.
The first run of bubblesort through our four numbers looks as follows:
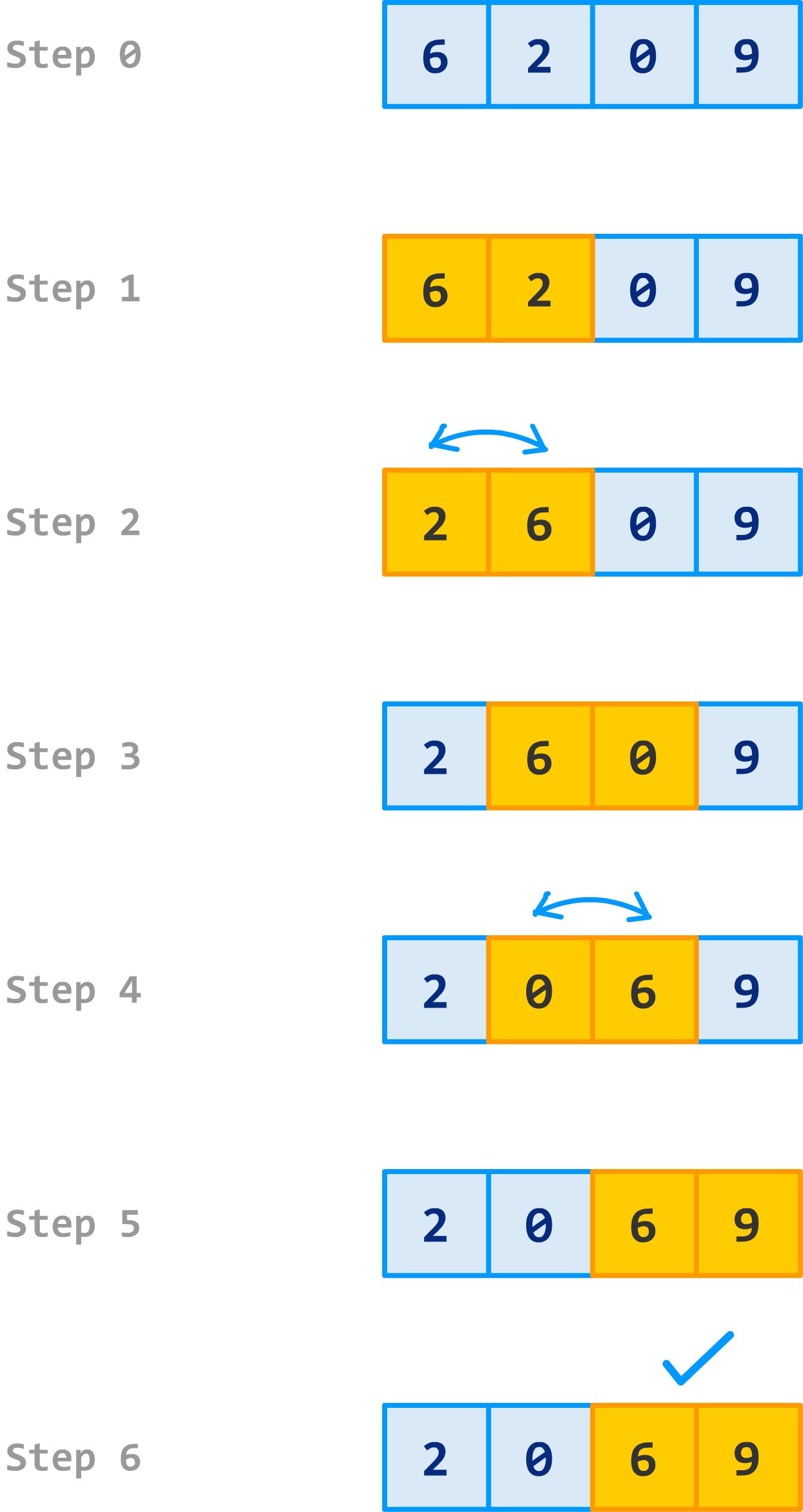
Now, we start at the beginning and do our old song and dance again:
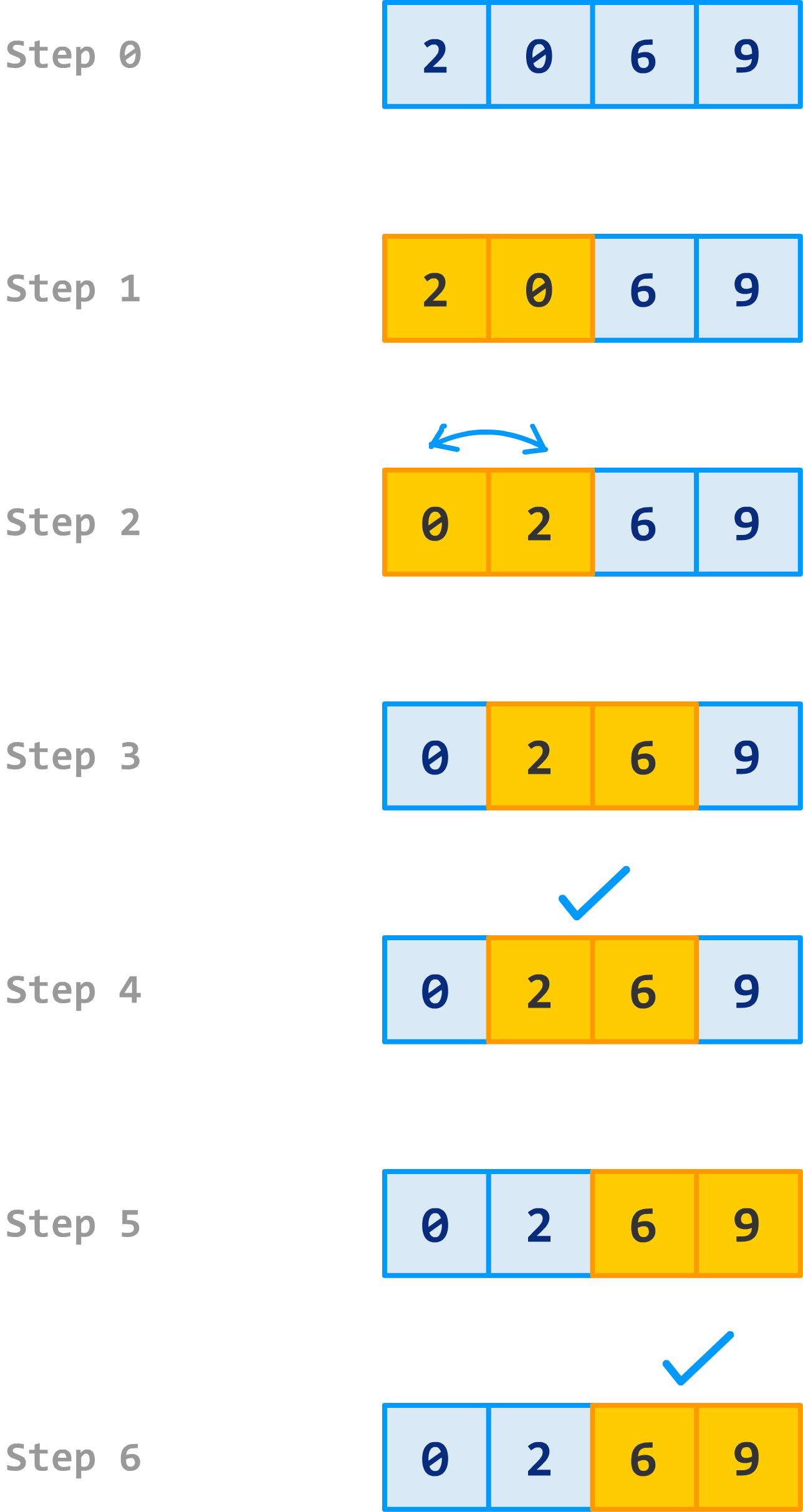
At this point, if we look at the results of the last step, our numbers are fully sorted. To us humans, we would call it a night and take a break. Bubble sort doesn't know that the numbers are sorted just yet. It needs to run through the numbers one more time to realize that when no swaps take place:
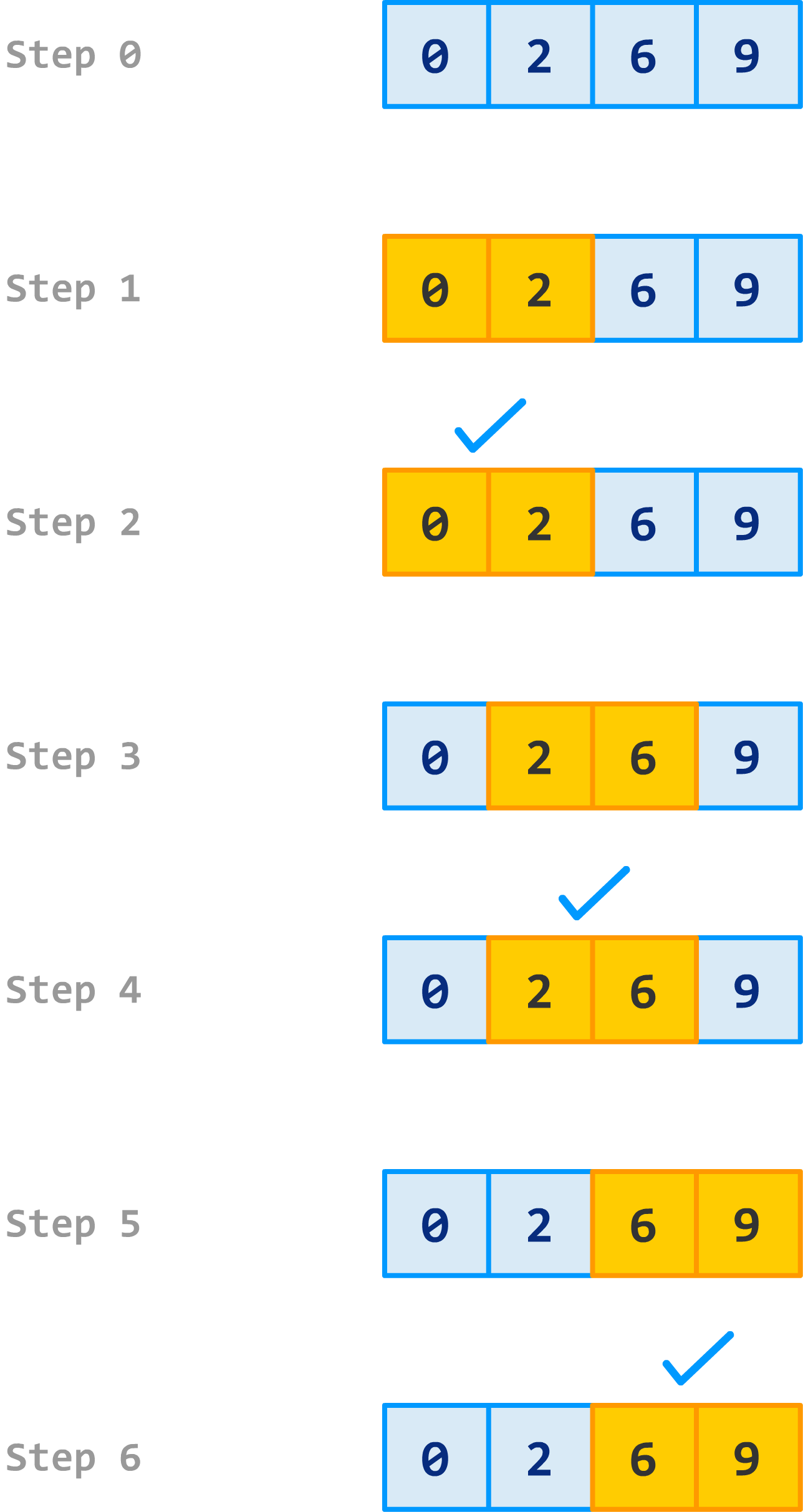
When no swaps happen, it means that every number is properly arranged. That signals to bubble sort to stop bothering these poor numbers and to go home.
Bubble sort is one of the slowest sorting algorithms out there. It cycles through the entire collection of unsorted values multiple times to eventually get to a sorted output. The following table describes the time and space characteristics:
| Scenario | Time Complexity | Memory Complexity |
|---|---|---|
| Best case | O(n) | O(1) |
| Worst case | O(n2) | O(1) |
| Average case | O(n2) | O(1) |
The best case happens when the entire collection of numbers is already sorted:
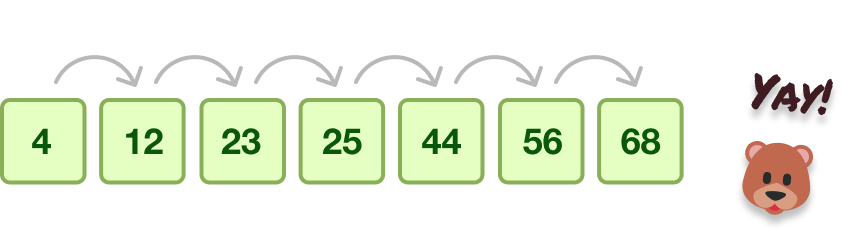
In this case, no swaps will ever need to take place so the algorithm will stop once it reaches the end of the collection after going through all of the items just once.
In both the average and worst case scenarios, the amount of time it will take on average to sort the numbers will be O(n2). At each iteration, the largest number in our unsorted collection will be swapped into the the right spot. What also happens at each iteration is that the number of comparisons we will need to also decreases by 1 since our collection gets more and more sorted.
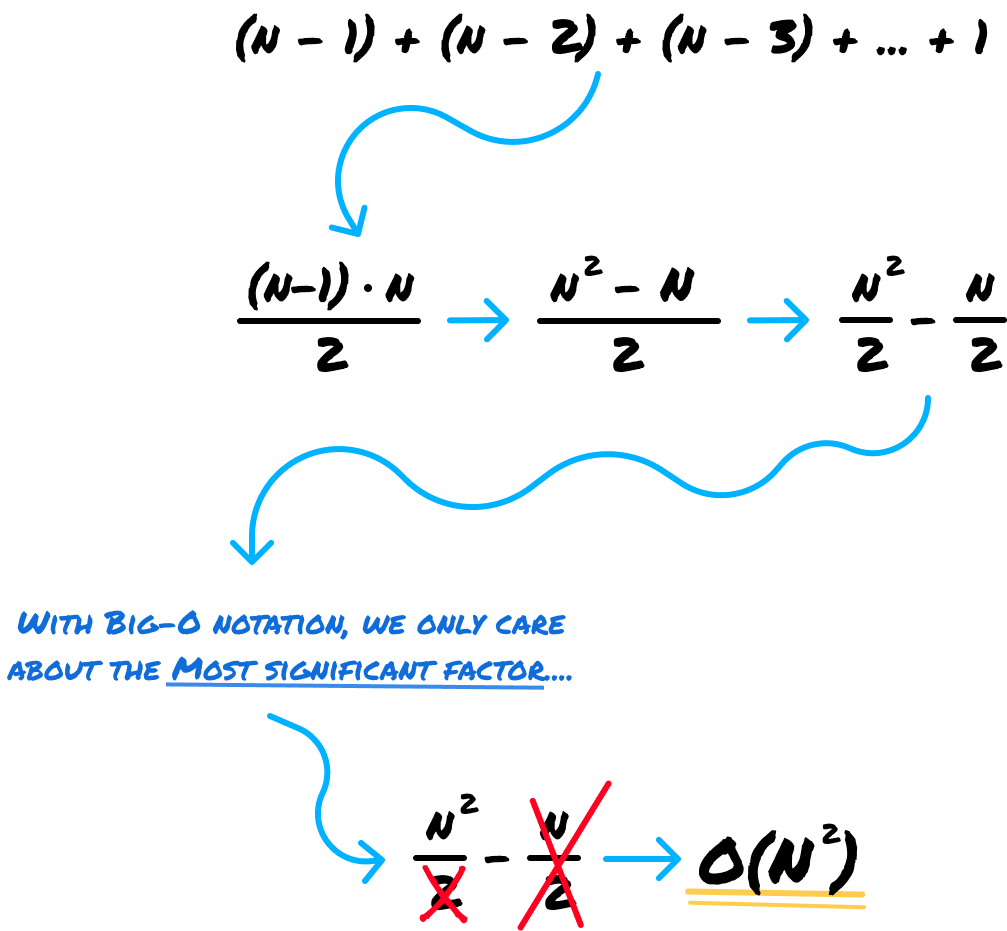
If we had to explain this mathematically, it would be as follows:
The total number of comparisons can be summarized as part of the famous arithmetic series, and the way we calculate the final Big-O notation is as follows:
The space complexity is much easier to reason about. The space taken up by bubble sort is constant. The reason for this is because we never introduce any new data structures to help in the sorting. The same input collection is the one we perform all of our comparison and swapping operations on.
Now that we've seen how bubble sort operates, let's take a look at one implementation of it:
function bubbleSort(input) {
let swapSignal = true;
while (swapSignal) {
swapSignal = false;
for (let i = 0; i < input.length - 1; i++) {
if (input[i] > input[i + 1]) {
let temp = input[i];
input[i] = input[i + 1];
input[i + 1] = temp;
swapSignal = true;
}
}
}
}
let myData = [6, 2, 0, 9, 1, 7, 4, 4, 8, 5, 3];
bubbleSort(myData);
console.log(myData);When we walk through this code, everything we see should map to what we looked at in the previous sections. The main thing to call out is the swapSignal variable that we use to indicate whether bubble sort has gone through these numbers without swapping any values. Besides that one thing of note, everything else is just simple array and for loop tomfoolery.
As you've seen from the walkthrough, bubblesort is not very efficient. For sorting four numbers, it took about 18 steps if you count the shifting and comparison as two individual operations. This was despite several numbers requiring no further sorting.
Bubble sort is fastest when you are already dealing with a fully sorted list of numbers. It goes through the numbers once, realizes that no numbers were swapped, and then heads over to the local discotheque and does some...discotheque-ing with all of the other cool kids. If you are dealing with a list of numbers that are sorted in reverse, bubble sort takes the longest amount of time. Every single number needs to be swapped and moved over to the end. I feel bad for whatever computing device has to deal with that reversed situation. The only sorting algorithm that would be worse than bubble sort would be Bogosort.
Before we call it a night (and join bubble sort at the local discotheque ourselves), below is a table comparing various popular sorting algorithms and their various performance and memory characteristics:
| Name | Running Time | Memory |
|---|---|---|
| Quicksort | O(n log n) | O(log n) |
| Mergesort | O(n log n) | O(n) |
| Heapsort | O(n log n) | O(1) |
| Timsort | O(n log n) | O(n) |
| Bubble sort | O(n2) | O(1) |
| Selection sort | O(n2) | O(1) |
| Insertion sort | O(n2) | O(1) |
| Counting sort | O(n + k) | O(n + k) |
| Radix sort | O(d ⋅ (n + k)) | O(n + k) |
You can find a more detailed comparison of these sorting algorithms as well as many others over on the Wikipedia section fully dedicated to this.
And with that, you are free to go and use your newfound knowledge to sort all sorts of things really REALLY slowly. If you want to learn about a fast sorting algorithm that leaves bubble sort behind in the dust, you really should become friends with quicksort.
Just a final word before we wrap up. If you have a question and/or want to be part of a friendly, collaborative community of over 220k other developers like yourself, post on the forums for a quick response!
:: Copyright KIRUPA 2024 //--