Table of Contents
As puzzles go, nobody really did it better than the monks who came up with the one we are going to learn about, the Towers of Hanoi. Besides being a really cool puzzle, it has a lot of practical (and historical!) significance as we learn about recursion.
Onwards!
Before we get to the programming side of things, let's first get a good idea of what the monks were trying to do. The objective of this puzzle is pretty simple. You have a series of disks and three pillars:
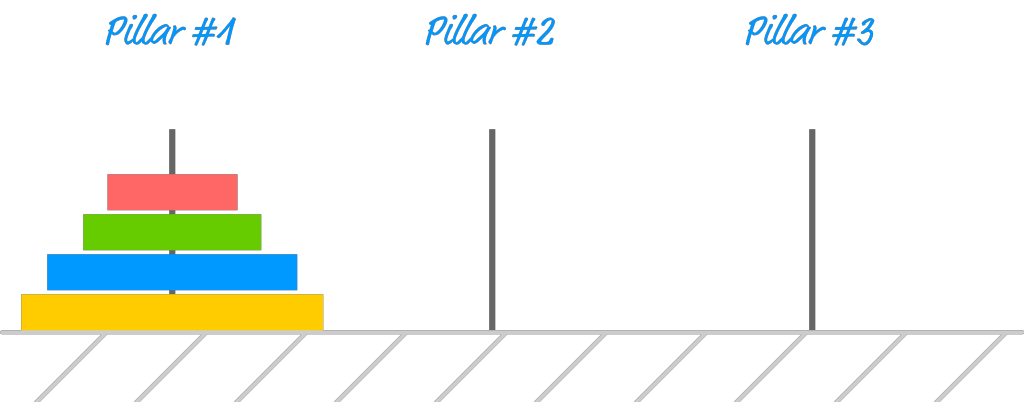
At the beginning, all of the disks are stacked on top of each other and start off in the first pillar. At the end, the stack of disks are shifted over to the last pillar:
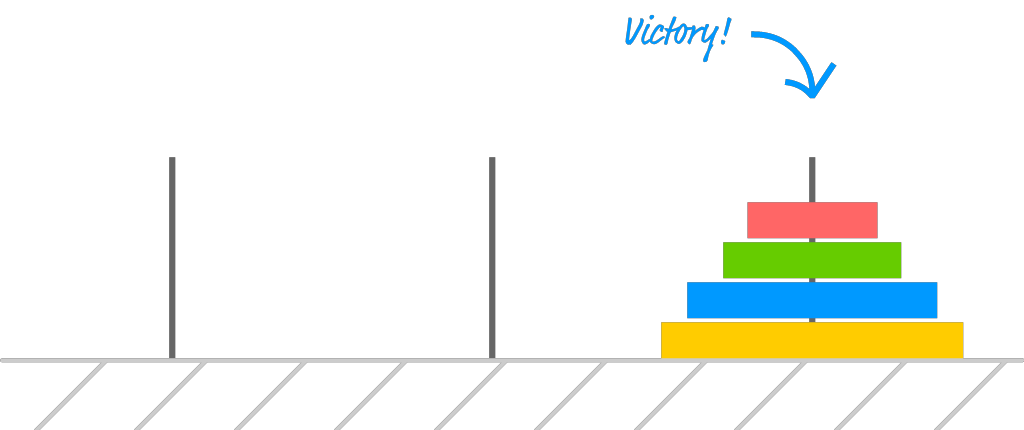
This seems pretty straightforward, but there are a few conditions that make things frustratingly complex:
These conditions probably don't make a whole lot of sense. To fix that, let's walk through a handful of examples and see how a typical game with these conditions is played.
The easiest way to play the game is to use a single disk:
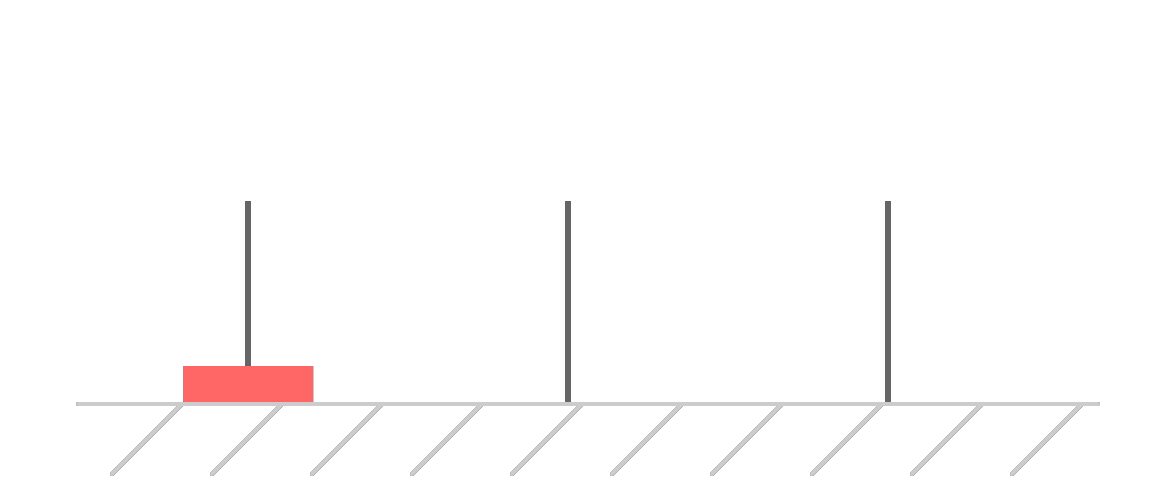
We have one disk at the beginning. Because there are no other disks to worry about, we can win in just one single move:
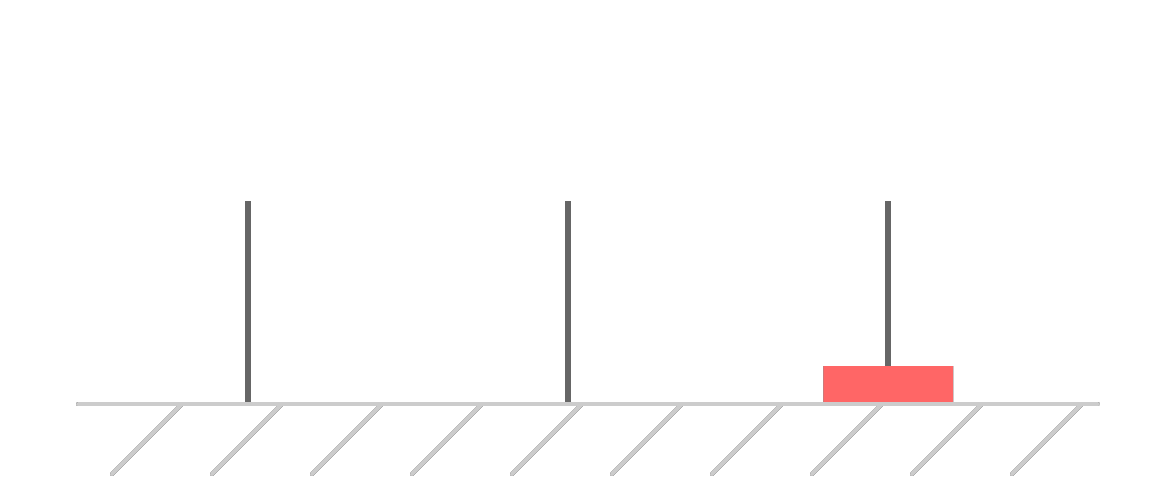
We can move our single disk directly to the destination without doing anything extra. With just a single disk, the puzzle isn't very challenging at all. To see what is really going on, we need more disks.
This time, let's start of with two disks:
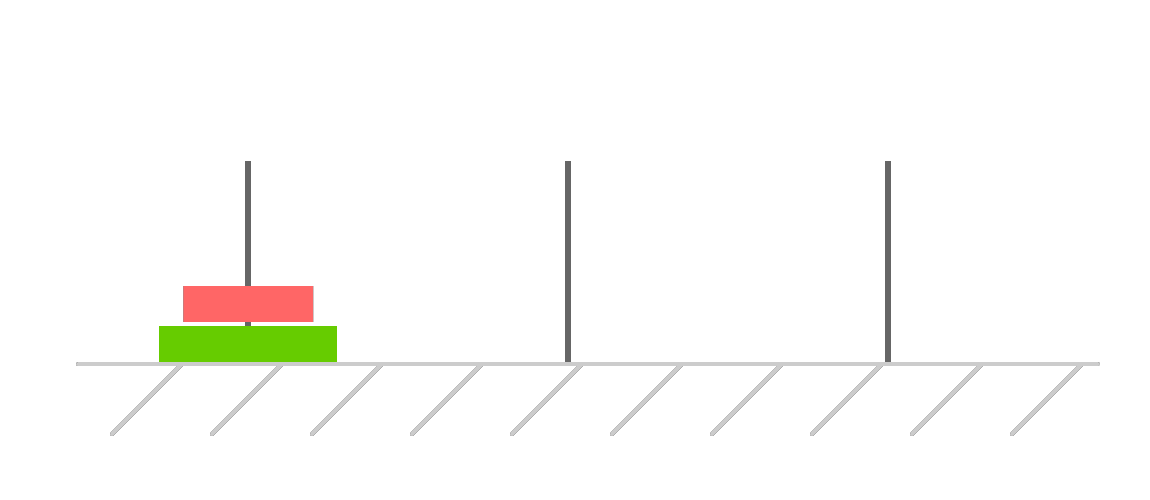
The goal of what we are trying to do is still the same. We want to shift these disks over to our destination, the third tower, while maintaining the same stacking order AND ensuring that a smaller disk is always placed on top off a larger disk at every move along the day.
This means, the first thing we need to do is clear a path for our larger disk to reach its destination. We do that by first shifting our top-most disk to our temporary, second tower:
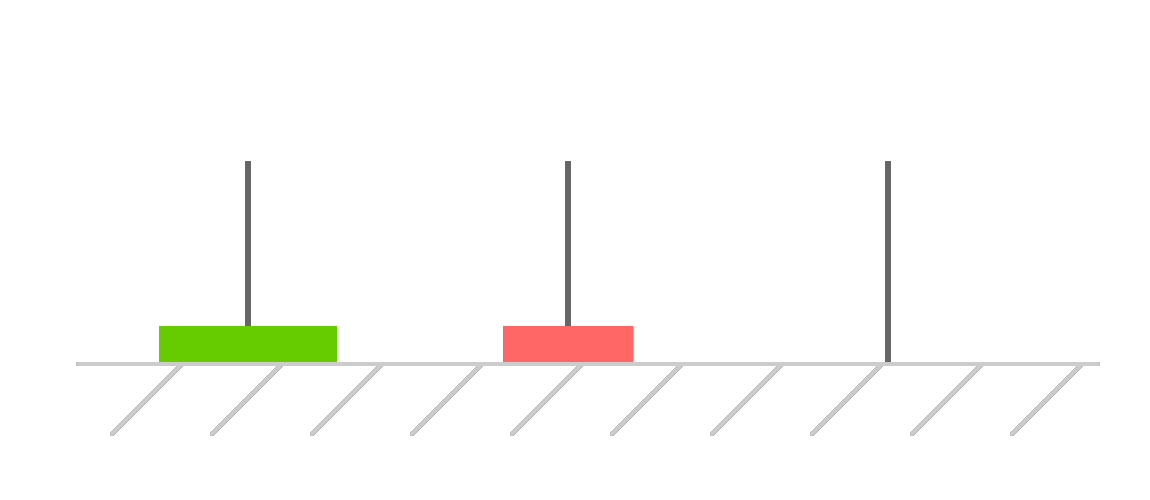
Once we've made this move, our larger disk has a direct path to the destination. This means our next move is to shift that disk over there:
The final step is to move our smaller disk from the temporary tower to the destination as well:
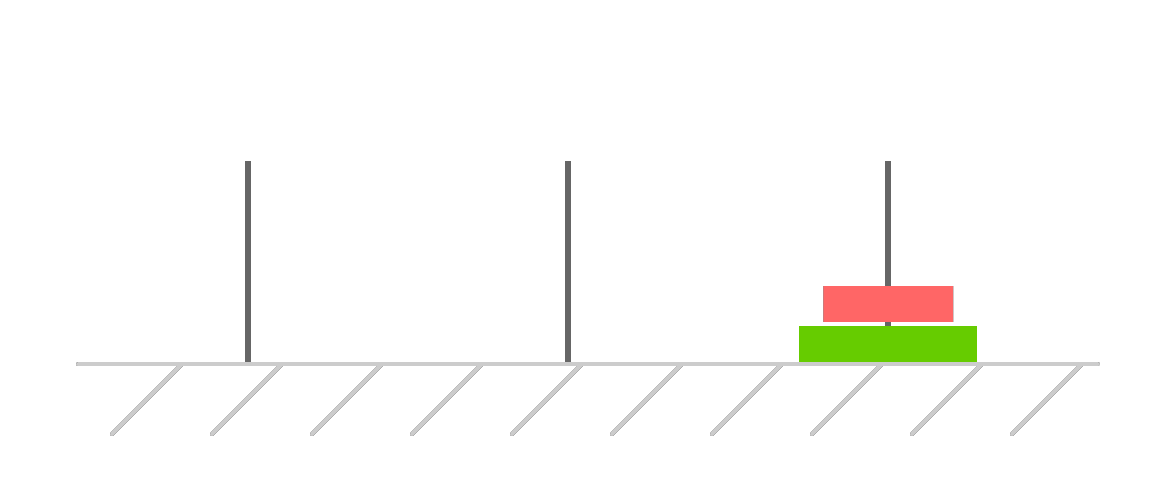
At this point, we've successfully shifted all of the disks from our starting point to the destination while respecting the various conditions. Now, with two disks we can see a little bit more about what makes this puzzle challenging. To really see the challenging-ness, we'll look at one more example in great detail. We are going to throw another disk into the mix!
All right. With three disks, the training wheels come off and we really see what the monks who inspired this puzzle were going against. We will start off with all of our disks at the starting point:
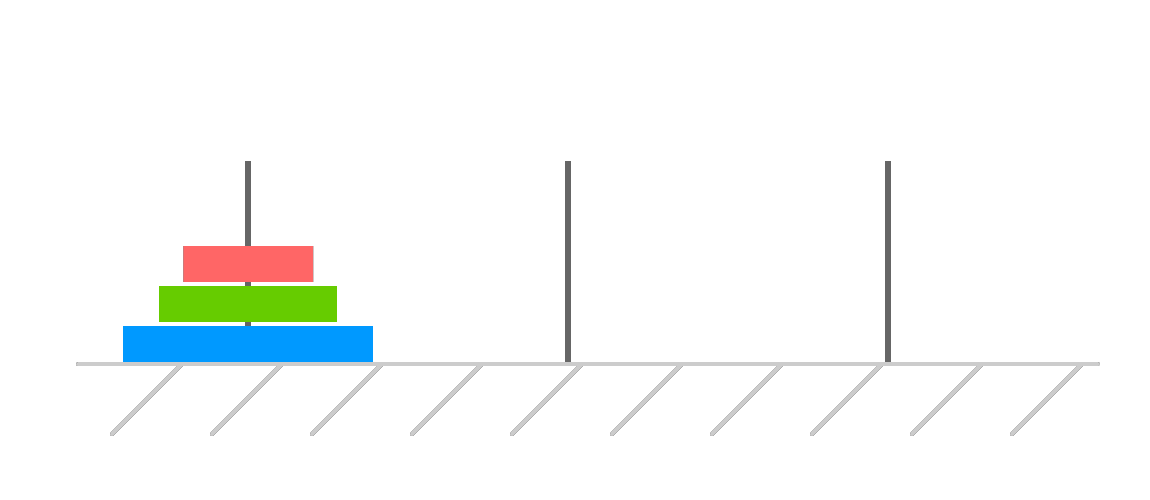
The first thing we are going to do is move our largest disk to the destination. This means we first move our smallest disk out of the way:
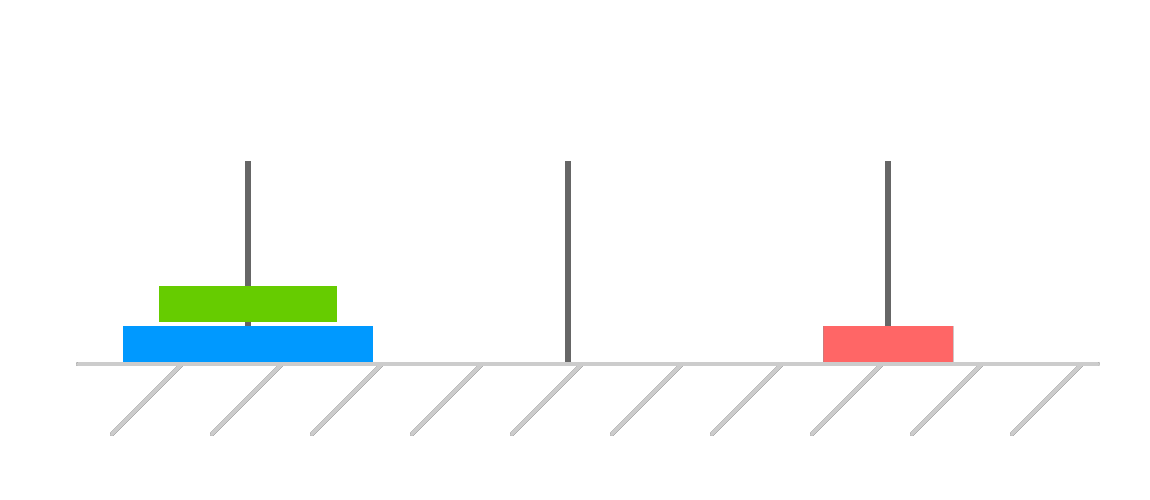
Wait, why is our smallest disk at our destination as opposed to our temporary tower? There is a technical reason for that. For now, let's just say that if you start off with an even number of disks, your smallest disk will move to the temporary tower first. If you start off with an odd number of disks, your smallest disk will move to the destination tower first.
Next, let's move our second disk over to the empty spot in our temporary tower:
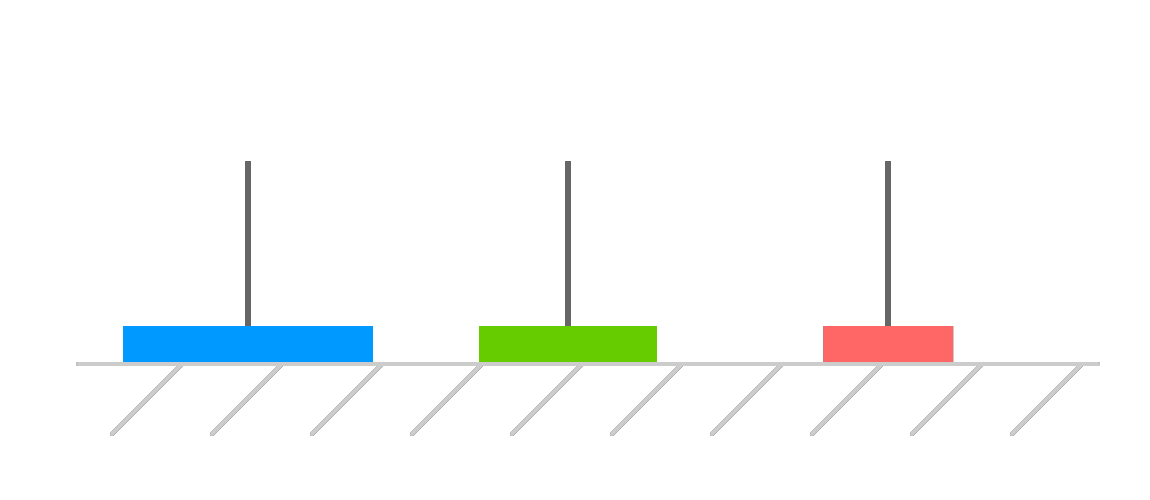
This leaves our third and largest disk almost ready to be moved to the destination tower. Our first disk currently stands in the way, but we can move that over to our temporary tower:
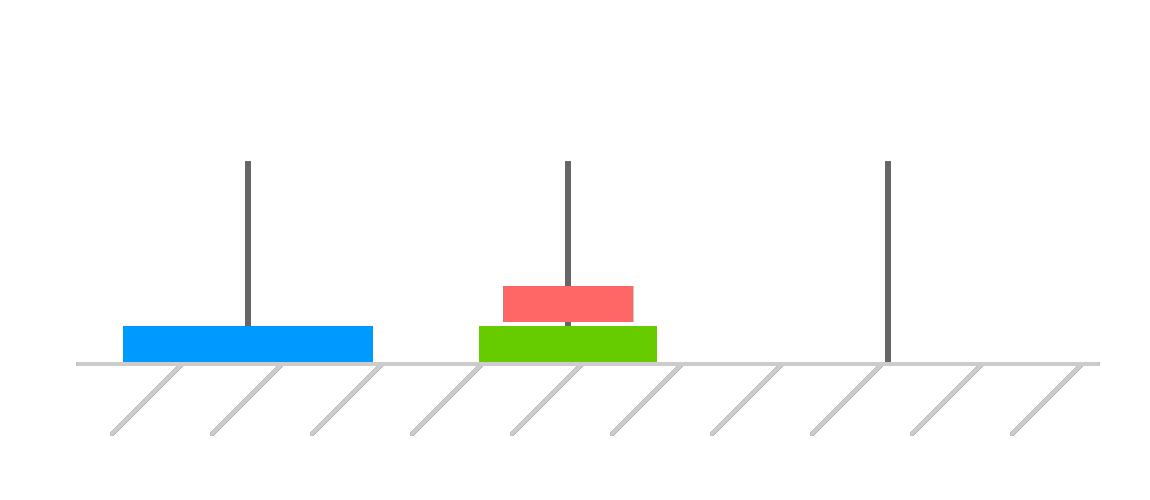
With the decks cleared, we move our third disk over to the destination:
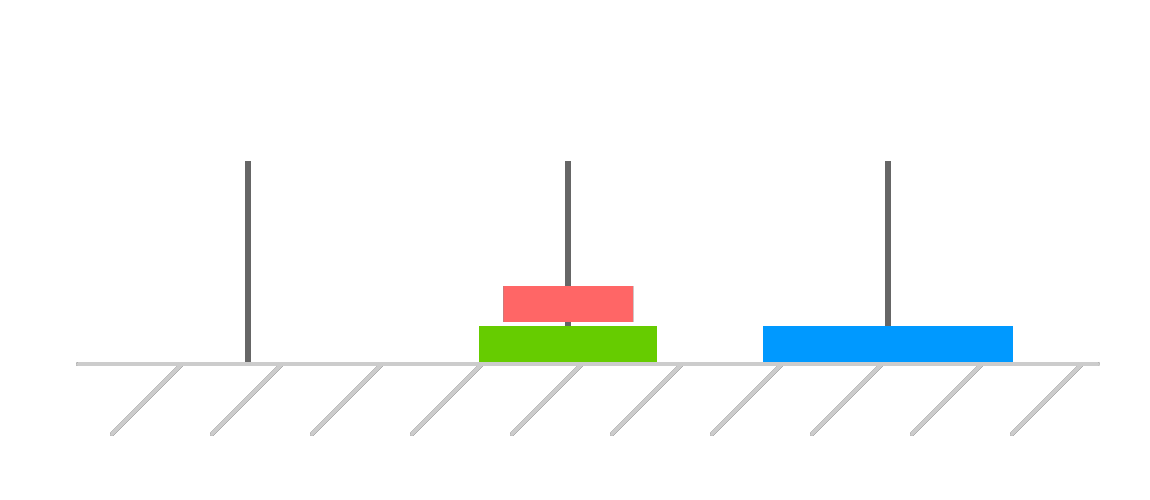
At this point, we have only have two disks in play. They are both in our temporary tower. What we do now is no different than what we started out doing earlier. We need to move our largest disk to the destination tower. This time around, that disk is our second one since our third disk is already safe at home in the destination tower. You may start to see a pattern emerging.
To make progress, let's move our top-most (and first...and smallest!) disk from our temporary tower over to our starting tower:
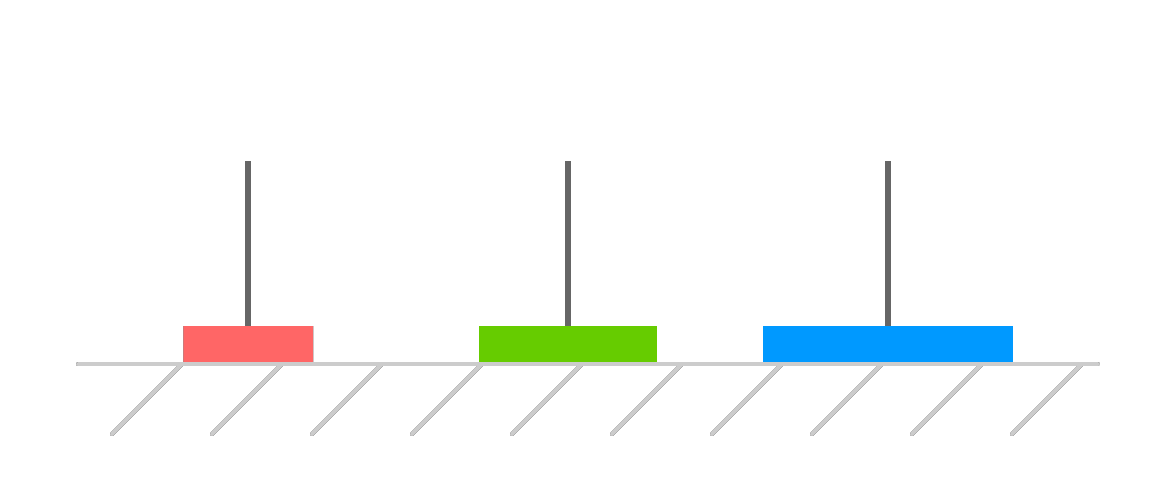
Next, let's move our second disk to the destination tower:
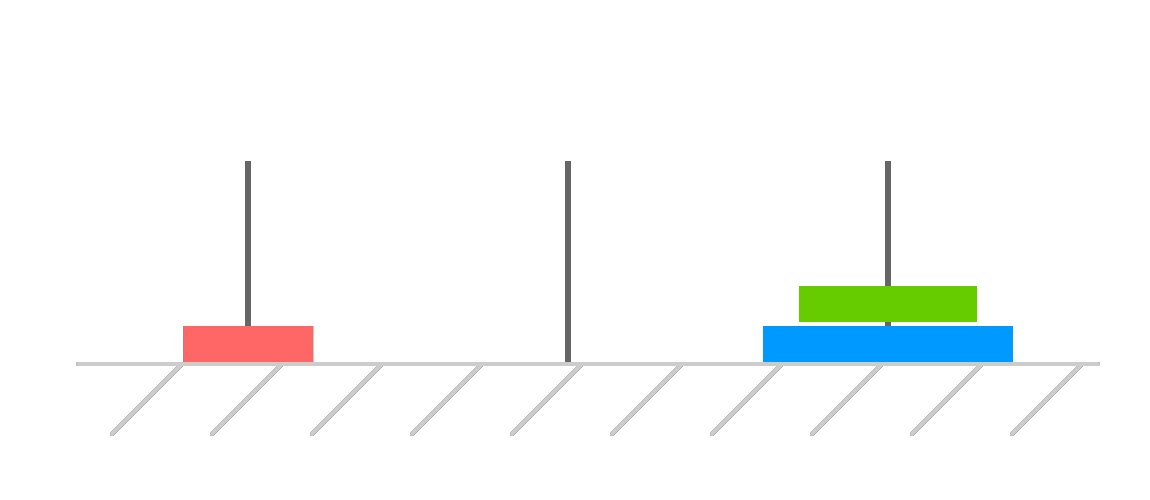
The remaining step is easy. We just have our first disk patiently waiting at the starting tower. Let's move it to the destination:
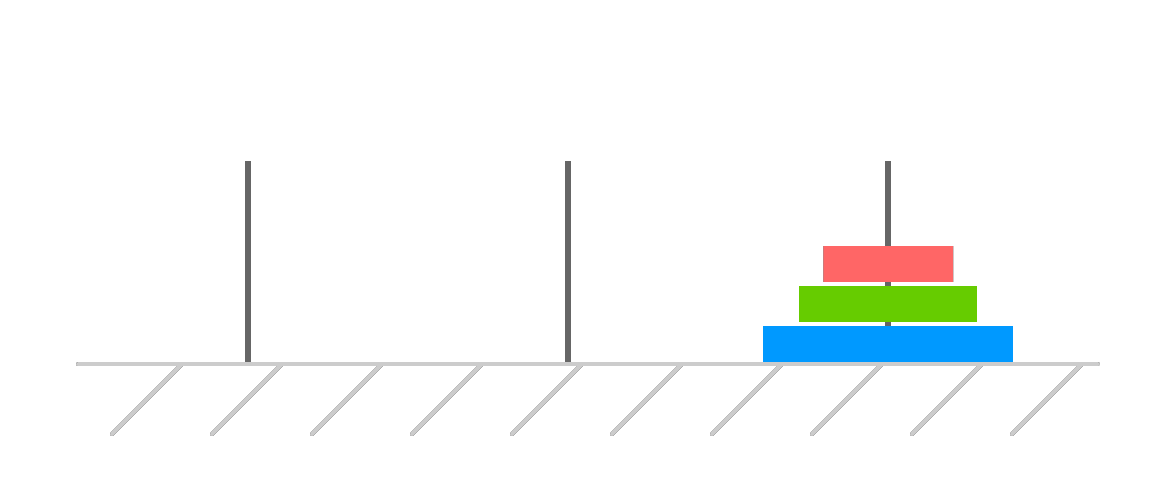
After all of this, we are now done moving three disks from our starting tower to the destination tower. We can repeat all of these steps for more disks, but we've seen all the interesting details to note about this puzzle by now. What we are going to do next is more formally look at all that this puzzle has going on and figure out how we can get our computers to solve it.
As humans, talking out loud and visually solving the problem totally works for us. Our computers are far less evolved. For them, we need to simplify our solution in terms that they understand. We can do that by restating what we know about how to solve this problem:
To state this a bit more formally, it will look like this:
There is one additional detail that is subtle but important to call out. The role our towers play while solving this puzzle is fluid. While we have given our towers strict names like starting, temporary, and destination, these names are really just helpful for us to understand what is going on. As part of moving the disks around, each tower will play an interim role as the temporary location, the destination location, or the starting location. For example, let's say you have a disk moving from the temporary tower to the destination:
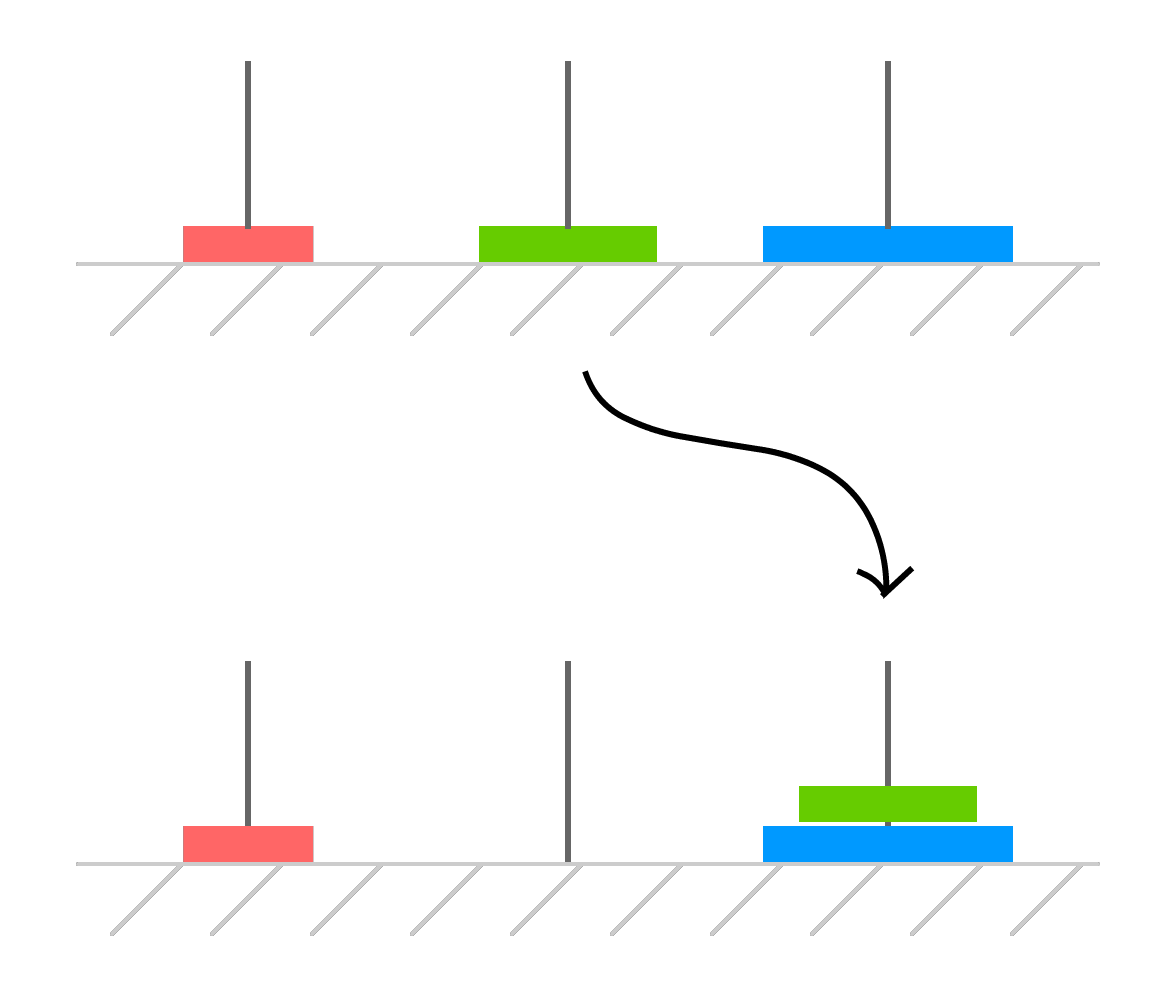
In this case, for just this move, our starting tower is really the temporary tower. The destination tower remains the same, but you can imagine the destination might be our starting tower in some intermediate step. It is this fluidity in our tower roles that makes it difficult for us to mentally make sense of this puzzle! But, it is exactly this fluidity that makes solving it using code much easier as well.
If we had to solve what we outlined in the three formal steps earlier, here is what one solution would look like:
var numberOfDisks = 3;
var hanoi = function(n, a, b, c) {
if (n > 0) {
hanoi(n - 1, a, c, b);
console.log("Move disk " + n + " from " + a + " to " + c + "!");
hanoi(n - 1, b, a, c);
}
}
hanoi(numberOfDisks,"starting", "temporary", "destination");
If you run this code for the three disks, what you'll see printed to the console will be as follows:
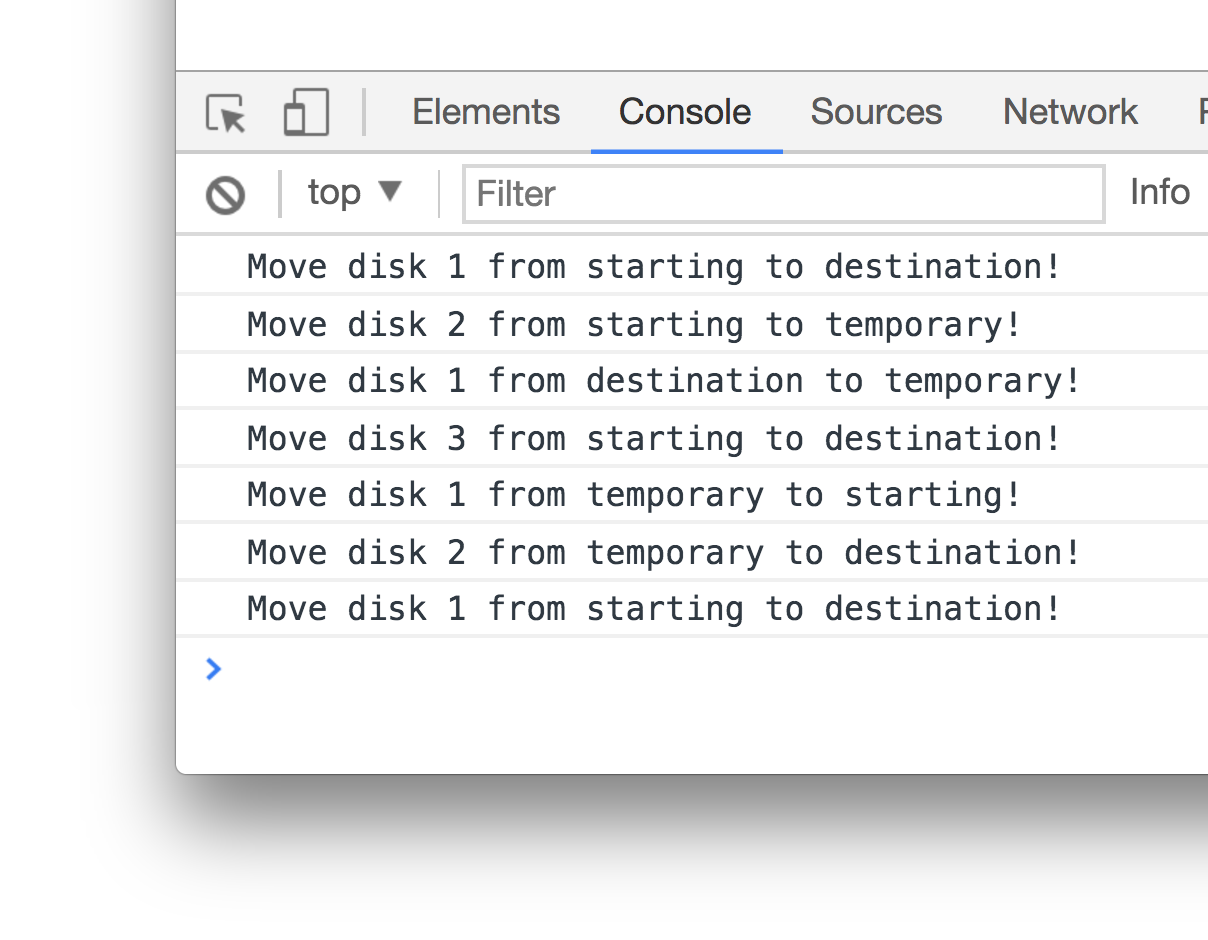
If you follow the path the output displays, you'll see what our code does to ultimately solve the puzzle for three disks. If you change the value for numberOfDisks from 3 to another (larger) number, you'll see a lot more stuff getting printed to your console. If you plot the path shown in the console, you'll again see what the solution looks like and the path each disk took in getting there. What we've just done is looked at the full code needed to solve our monks' Towers of Hanoi puzzle. We aren't done yet, though. Let's look at at this solution in greater detail for a few moments.
If you take a quick glance at the code, you can tell that our solution is a recursive one:
var numberOfDisks = 3;
var hanoi = function(n, a, b, c) {
if (n > 0) {
hanoi(n - 1, a, c, b);
console.log("Move disk " + n + " from " + a + " to " + c + "!");
hanoi(n - 1, b, a, c);
}
}
hanoi(numberOfDisks,"starting", "temporary", "destination");
Our hanoi function is really solving the sub-problem of moving N-1 disks from one location to another. This function keeps getting called until the disk you are on is your last disk (aka n > 0).
If we had to draw out the full recursive call for three disks, what you'll see will look as follows:
hanoi(3, starting, temporary, destination)
hanoi(2, starting, destination, temporary)
hanoi(1, starting, temporary, destination)
hanoi(0, starting, destination, temporary)
// Move disk 1 from starting to destination!
hanoi(0, temporary, starting, destination)
// Move disk 2 from starting to temporary!
hanoi(1, destination, starting, temporary)
hanoi(0, destination, temporary, starting)
// Move disk 1 from destination to temporary!
hanoi(0, starting, destination, temporary)
// Move disk 3 from starting to destination!
hanoi(2, temporary, starting, destination)
hanoi(1, temporary, destination, starting)
hanoi(0, temporary, starting, destination)
// Move disk 1 from temporary to starting!
hanoi(0, destination, temporary, starting)
// Move disk 2 from temporary to destination!
hanoi(1, starting, temporary, destination)
hanoi(0, starting, destination, temporary)
// Move disk 1 from starting to destination!
hanoi(0, temporary, starting, destination)
I get that this doesn't look very nice, but take a moment to follow through with what is going on. Especially pay close attention to us swapping the values for where a disk needs to end up by jumping between the starting, temporary, and destination towers. The end result of all of this is still the same: our disks move from their starting point to the destination without breaking those annoying rules :P
According to the legend, the monks are not moving a handful of disks. They are moving 64, and it takes them one second to make a single move. I'm guessing these monks were pretty buff. Anyway, to better help them plan, let's figure out how many moves it will take for them to move all 64 disks. For figuring that out, we are going to throw some math into the mix.
For 1 disk, the number of moves to complete the puzzle was 1. For two disks, the number of moves was 3. For three disks, the number of moves was 7. For zero disks, the answer is of course, 0. If you tested with 4 disks, the number of moves (if you count the output in your console perhaps) to complete moving all the disks is 15.
You should start to see a pattern for the number of moves needed to complete the puzzle for a given number of disks:
To figure out the number of moves for any arbitrary number of disks, after experimenting with a few guesses, the formula would be 2n - 1. We can go even more detailed in our analysis if you don't like coming up with the formula by finding patterns in the output.
From our code (and our rules), we know that there are three distinct steps:
Steps 1 and 3 take Tn-1 moves each. Step 2 takes just 1 move. We can state all of this as:
Tn = 2Tn-1 + 1
This is the number of total moves involved in solving the puzzle where n stands for the number of disks. For T0 we know the number of moves is 0. For T1 we know the number of moves is 1. Extending this to our above formula, we can do something like the following:
T0 = 0
T1 = 2T0 + 1 = 2(0) + 1 = 1
T2 = 2T1 + 1 = 2(1) + 1 = 3
T3 = 2T2 + 1 = 2(3) + 1 = 7
This seems to check out, so let's prove that this form maps to the Tn = 2n - 1 equation figured out earlier. Let's assume that this formula holds for n - 1. This would mean that our equation could be re-written as Tn-1 = 2n-1 - 1.
Let's combine this with what we looked at earlier:
Tn = 2Tn-1 + 1
Tn = 2(2n-1 - 1) + 1
Tn = 2(2n-1) - 2 + 1
Tn = 2(2n-1) - 2 + 1
Tn = 2n-1+1 - 1
Tn = 2n - 1
This proves out that the answer we came up with earlier holds for all ranges n where n is 1 or greater. This is a less rigorous form of an induction proof that doesn't dot all the i's and cross the t's, so don't use this as the proof is you are asked to formally prove it.
Do you know why the monks were moving 64 disks in the first place? They believed that the world would end once the last disk was placed in its rightful location. If that were true, how long do we all have? Using the formula we have for the number of moves, and knowing from legend that each move takes one second, how long will our monks take to complete the puzzle? Unfortunately for them, using the 264 - 1 formula we have, the amount of time it will take them is somewhere around 585 billion years. That's good for us, though! To learn more about the history of this puzzle and the French mathematician who Édouard Lucas who actually introduced it to everyone, go here.
Just a final word before we wrap up. If you have a question and/or want to be part of a friendly, collaborative community of over 220k other developers like yourself, post on the forums for a quick response!
