There are many (totally work-safe!) words people use to describe sorting algorithms. One such word is stability. Some sorting algorithms are stable, and some sorting algorithms are far from it. In this short tutorial, we'll explain what stability in the context of sorting algorithms means and walk through an example.

Onwards!

Of Stability and Un-Stability

Stability refers to a property that some sorting algorithms have where the relative order of equal elements in the sorted output is the same as their relative order in the original unsorted input. This may be a bit convoluted, so let's simplify this with an example. In our example, we start off with an unsorted list of values made up of a person's name and age:

What we want to do is sort our list based on age, starting with the lowest value at the top. Notice that two items in our list have the same value. Both Alice and Michael are 22 years old. In a stable sorting algorithm, when we perform our sort, the order of Alice and Michael will remain the same as what they are in their current unsorted list:

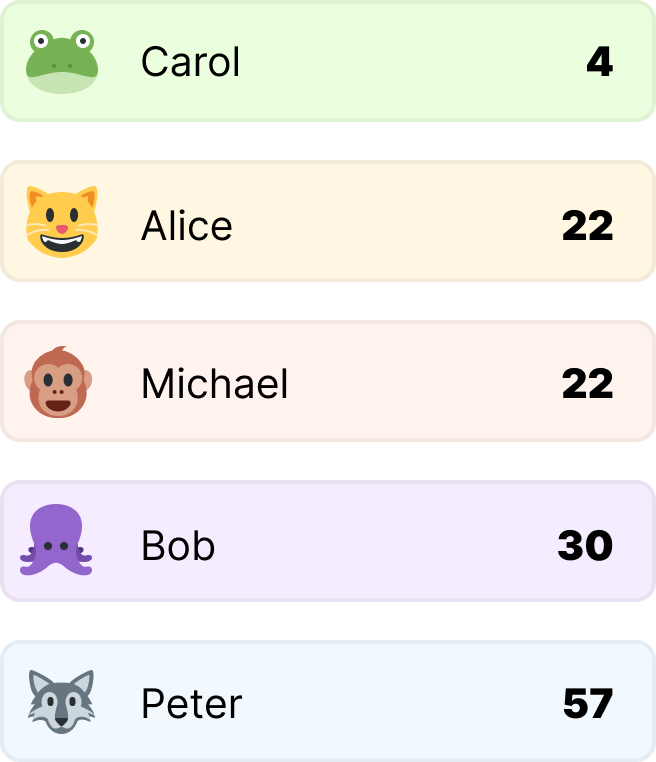
In other words, our unsorted list had Alice appearing before Michael. In our sorted list, Alice continues to appear before Michael. Stability achieved:

If we had instead used an unstable algorithm, we would have seen an outcome similar to the following:

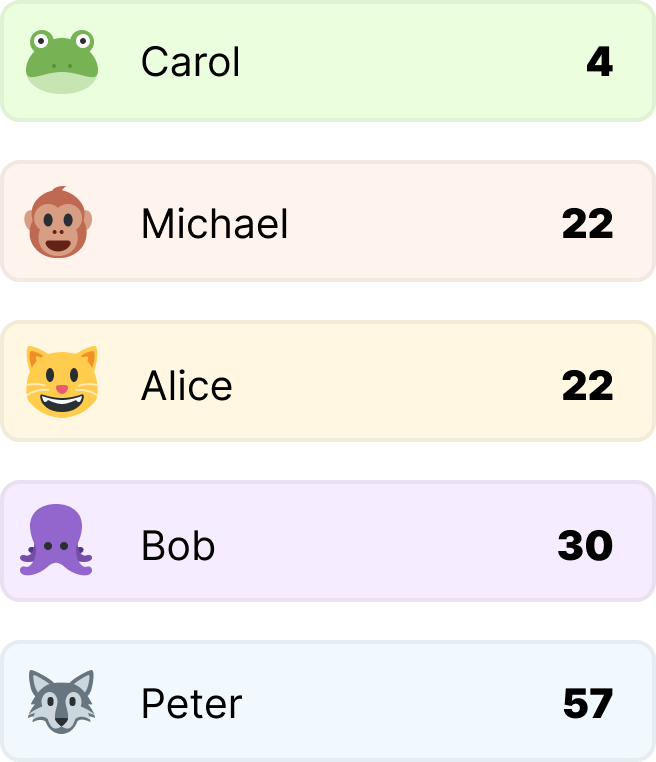
In this case, the relative order of Alice and Michael has changed compared to the original input. This is an example of an unstable sorting algorithm. Even though Alice and Michael are the same age, their order in the sorted output is not guaranteed to match their order in the input.

Sorting Algorithm Stability Showdown

Which sorting algorithms make the cut on the stability front? Take a look at the following table and the more detailed explanation below for the answer:

Sorting Algorithm	Stability
Bubble Sort	Stable
Selection Sort	Unstable
Insertion Sort	Stable
Merge Sort	Stable
Quick Sort	Unstable
Heap Sort	Unstable
Counting Sort	Stable
Radix Sort	Stable
Tim Sort (a hybrid)	Stable

More detailed explanation:

1. Bubble Sort: Bubble Sort is a stable sorting algorithm. It compares adjacent elements and swaps them if they are out of order, but it does not change the relative order of equal elements.

2. Selection Sort: Selection Sort is an unstable sorting algorithm. It repeatedly selects the minimum element and places it at the beginning of the sorted portion, which may change the relative order of equal elements.

3. Insertion Sort: Insertion Sort is a stable sorting algorithm. It builds the sorted portion of the array one element at a time, preserving the relative order of equal elements.

4. Merge Sort: Merge Sort is a stable sorting algorithm. It divides the array into smaller parts, sorts them, and then merges them back together while maintaining the relative order of equal elements.

5. Quick Sort: Quick Sort is generally considered unstable. It involves partitioning the array based on a chosen pivot, and the pivot's choice can affect the relative order of equal elements.

6. Heap Sort: Heap Sort is usually considered unstable. It uses a binary heap data structure to sort elements and may change the order of equal elements.

7. Counting Sort: Counting Sort is a stable sorting algorithm. It counts the occurrences of each element and then reconstructs the sorted order, maintaining the relative order of equal elements.

8. Radix Sort: Radix Sort is a stable sorting algorithm. It sorts elements by considering their digits in a specific radix (base), preserving the relative order of equal elements.

9. Tim Sort: Tim Sort is a hybrid sorting algorithm based on Merge Sort and Insertion Sort. It is designed to be stable, and it uses various techniques to ensure stability in sorting.

One thing to note is that, while these characteristics are generally true for these sorting algorithms, some specific implementations may deviate a bit. It's best to double-check the implementation.

For the sorting algorithm implementations you encounter on this site, though, the stability table is totally accurate!

Conclusion

In far too many situations, the stability of a sorting algorithm can be crucial. It may seem unnecessary when we look at an example of some age values being sorted, but imagine sorting a list of values whose initial order is critical as part of managing a queue. Any changes in the order can have negative consequences. This is especially multiplied if our data goes through multiple rounds of sorting. A combination of sort (and maybe even merge!) operations involving stable and unstable sorting algorithms will reduce the predictability of the final output. None of these are great.

Just a final word before we wrap up. If you have a question and/or want to be part of a friendly, collaborative community of over 220k other developers like yourself, post on the forums for a quick response!