Table of Contents
It's time for us to look at another awesome data structure, the binary search tree. If we squint at a binary search tree from a distance, it will look a whole lot like a binary tree:
That’s by design. Binary trees set a solid foundation with their node/edge rules and branching behavior that is desirable. Binary search trees improve upon plain binary trees by adding some extra logic on how they store data, and it is this extra logic that helps make them quite efficient when dealing with the sorts of data operations we may throw it.
At a very high level, a binary search tree is designed in such a way that the location of each node is determined based on the size of the value it is storing. Nodes with smaller values go left, and nodes with larger values go right. Take a look at the following binary search tree:
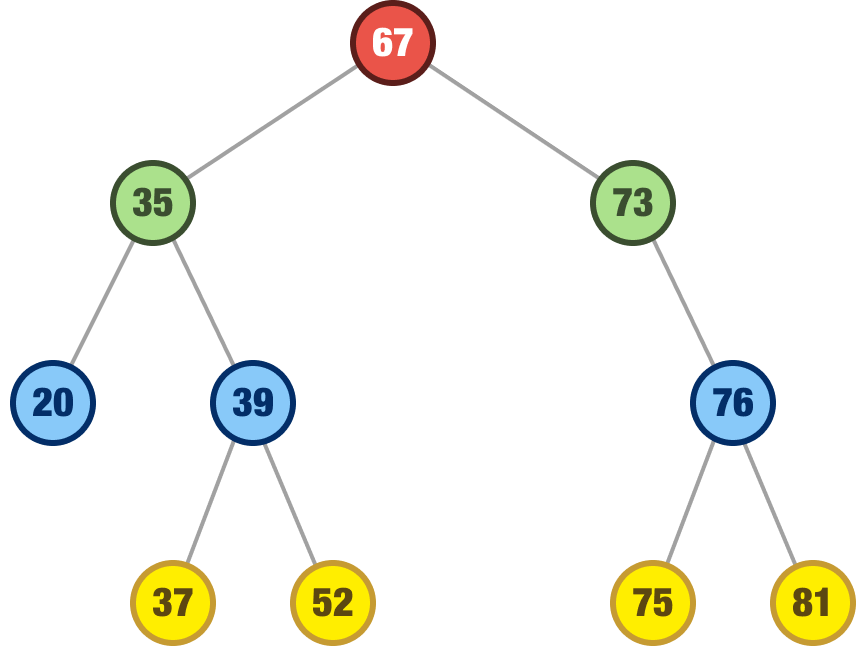
At each node, starting with the root, pay close attention to the node values and the values of their children, if applicable. At each layer:
These two additional rules build on the three rules we saw for plain binary trees to give us our blueprint for how to think about binary search trees. What we are going to do next is dive deeper into how binary search trees work by looking at how to perform common add and remove operations.
Onwards!
When looking at the unique properties of trees, it is easy to get caught up in the weeds. If we take many steps back, a tree is just a data structure like our arrays, stacks, queues, linked lists, and more. It exists to help us manipulate or make sense of data. In the following sections, let’s look at binary search trees and how we would add data to them, remove data from them, and more.
To help with this, we are going to start at the very top with a blank slate:
Yes, that’s right! We are going to start with an empty binary search tree and build our knowledge of how to work with them from there.
What we are going to do is have our binary search tree store some numbers. The first number we want to store is 42, and this is what our binary search tree will look like after we have added it:
It doesn’t look like much of a tree, and that is because our binary search tree was empty. What we have is just a single node (which also happens to be the root!) with a value of 42.
Next, let’s add the number 24. Every new node we add from here on out has to be a child of another node. In our case, we only have our root node of 42, so our 24 node will be a child of it. The question is, will it go left, or will it go right?
The answer to this is core to how binary search trees work. To restate what we mentioned earlier:
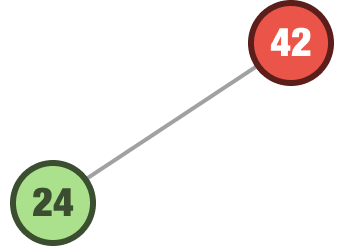
We start at the root node and start looking around. In our case, we only have one node, the root node of 42. The number we are trying to add is 24. Since 24 is less than 42, we will add our node as a left child:
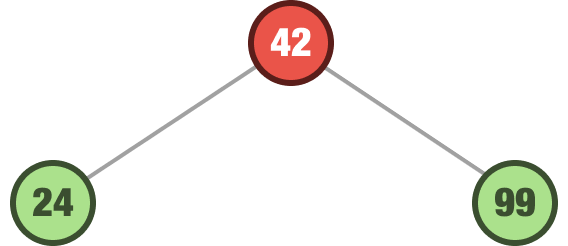
Let’s add another number. This time, the number we want to add is 99. We follow the same steps as earlier. We start at the root. The value we are adding is 99, and it is greater than node we are at. It goes right:
We are not done with adding more numbers to our tree. Now that we have a few extra nodes beyond just our root node, things get just a tad bit more interesting. The next number we want to add is 15. We start at the root. The root value is 42, so we look left since 15 is less than 42. Left of 42 is the 24 node. We now check if 15 is less than 24 or not. Since 15 is less than 24, we look left again. There are no more nodes to the left of 24, so we can safely park 15 there:
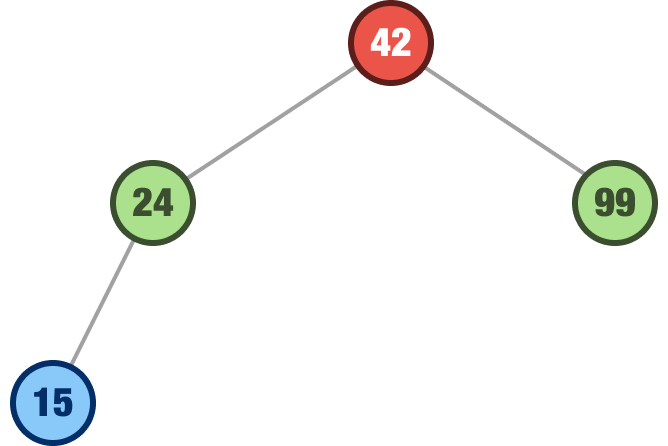
You should see a pattern starting to emerge. When adding a new node, we ask our “Is the value greater than or less than the current node?” question at each node we encounter starting at the root. If we encounter a leaf node, this node now becomes our parent. Whether we are a child at the left position or right position is, again, based on whether the value of the node we are adding is less than or greater than our new parent.
We will go a bit faster now. The next value we want to add is 50. We start with our root node of 42. Our 50 value is greater than 42, so we look right. On the right, we have our 99 node. 99 is greater than 50, so we look left. There is no node to the left of our 99 node, so we plop our 50 value there:
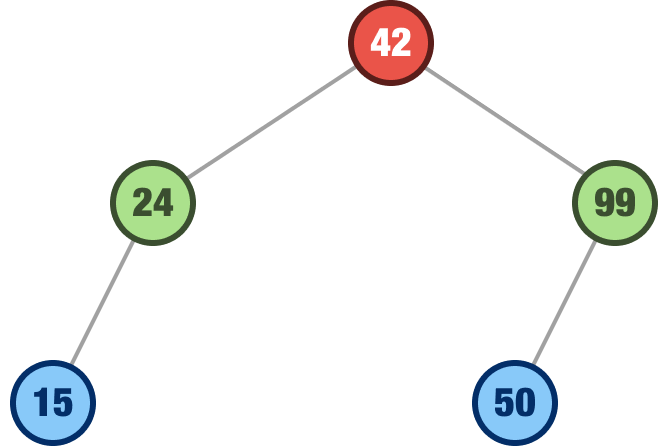
The next value we want to add is 120. Using the same steps we’ve seen a bunch of times, this value will find itself to the right of the 99 node:
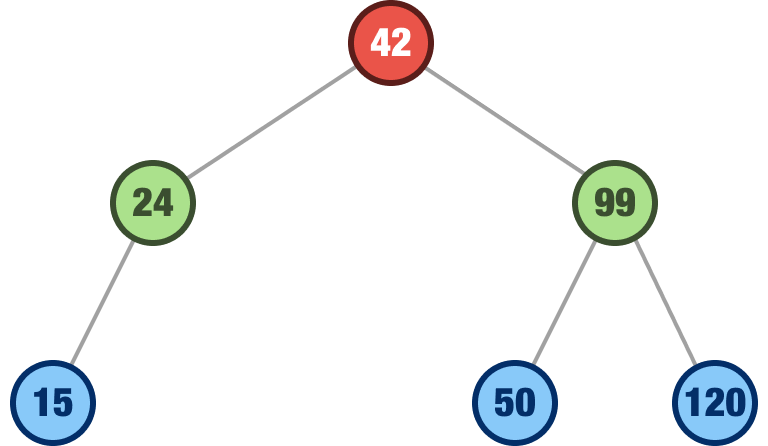
The last number we are going to add is the number 64. Take a moment to see where it will land. If everything goes as planned, it will find itself as a right child of the 50 node:
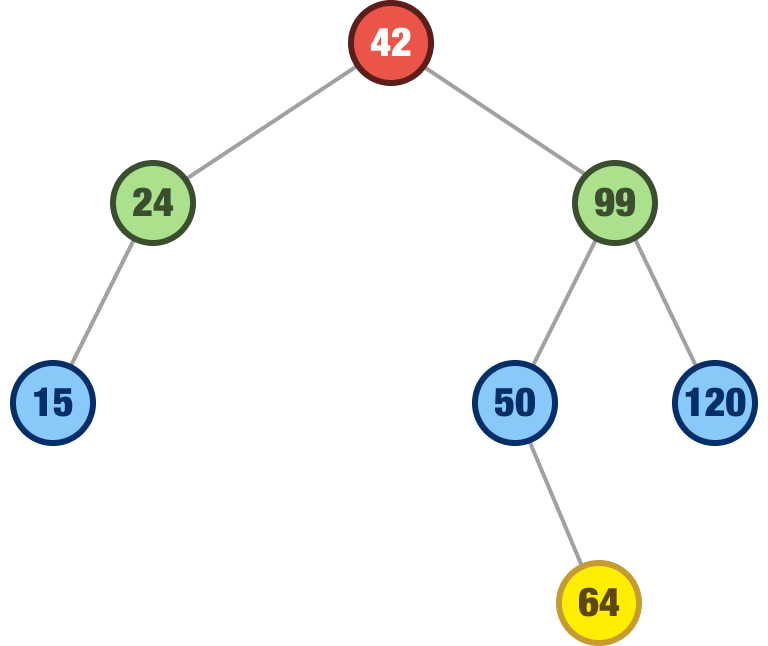
Walking through our steps, we know that 64 is greater than our root node of 42. It is less than our 99 node, so we look left where we have the 50 node. 64 is greater than 50, so right of it...it goes!
By now, we have looked at a bunch of examples of how to add nodes to our binary search tree. The biggest thing to note is that every node we add ends up as a leaf somewhere in our tree. Where exactly it ends up is determined solely based on its value and the value of the various nodes starting at the root that it needs to navigate through.
There will be times we’ll be adding nodes. Then there will be times we will be removing nodes as well. Removing nodes from a binary search tree is slightly more involved than adding nodes, for the behavior varies depending on which node we are removing. We’ll walk through those cases next.
If the node we are trying to remove is a leaf node, this is straightforward. Continuing our binary search tree example from earlier, let’s say we want to remove our leaf node with the value of 64:
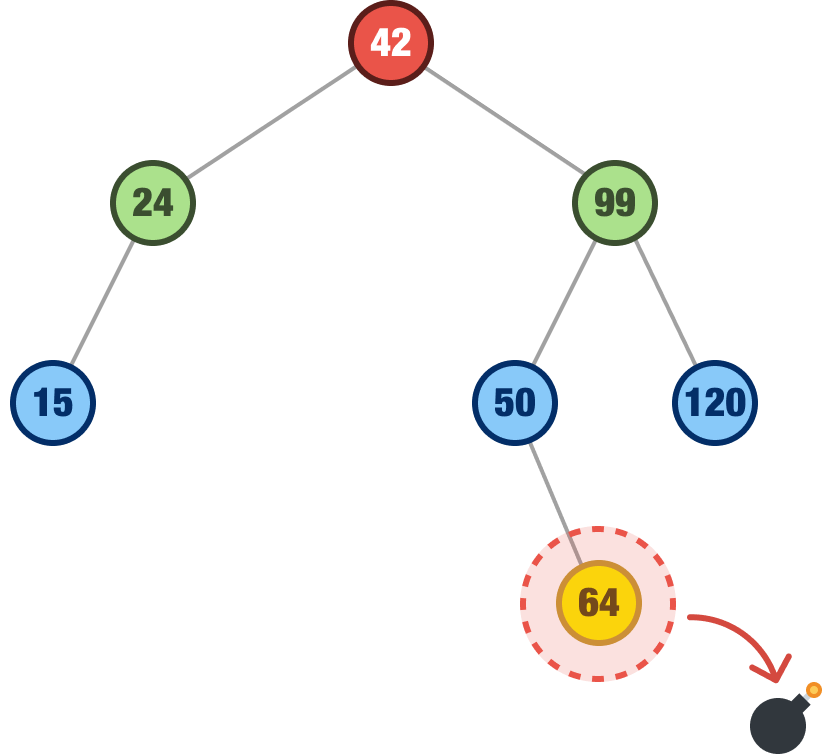
When we remove it, well...it is removed. That’s it:
There is nothing else for us to do. Because it is a leaf node, nothing else in our tree is impacted. That won’t be the case with what we are going to see next.
Removing a leaf node was straightforward. We just removed it. What if we are not removing a leaf node. Instead, we are removing a node that has a single child. For example, let’s say we want to remove the node with the value of 24:
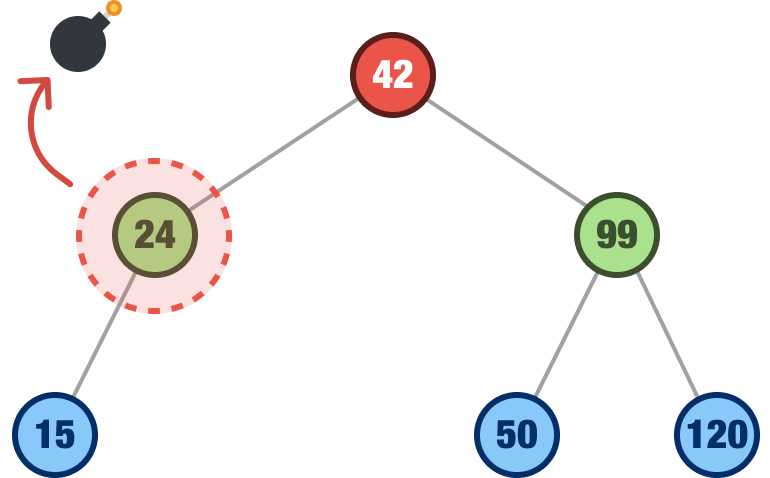
When we remove a node with a single child, that child takes the place of the removed node. In our example, when we remove the 24 node, the 15 node will take its place:
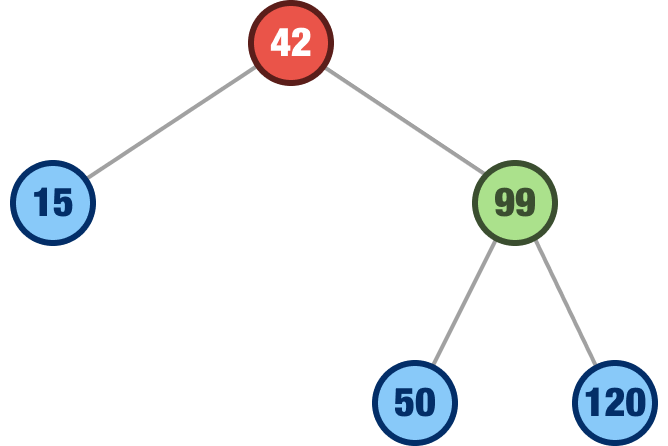
Because of how we add nodes to our binary search tree in the first place, promoting a child node to its parent position will not break the overall integrity of our tree, where values to the left of each node are smaller than values to the right of each node.
There is another point to clarify. When we are talking about the behavior of deleting a node with a single child, we mean a single immediate child. Our immediate child can have more children of its own. Take a look at the following example:
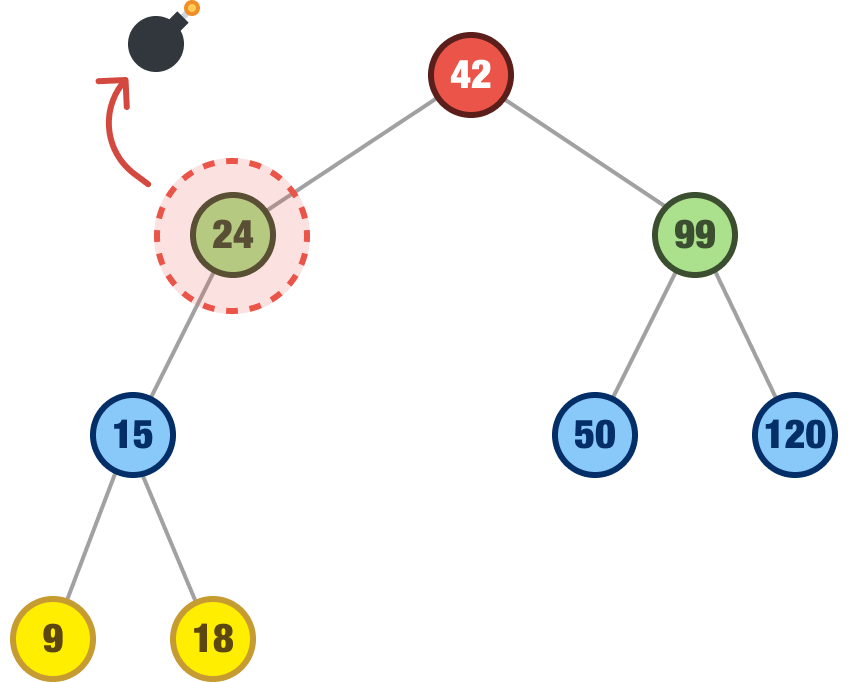
We want to remove our 24 node, and it has the 15 node as its child. The 15 node has two children of its own, but this detail doesn’t change the behavior we are describing. As long as the parent node we are removing only has a single immediate child, that single immediate child will take the parent’s place and bring along any children it may have as well:
If we walk through all the nodes in the tree after this shift, we’ll again see that the integrity of the tree is still maintained. No node is out-of-place.
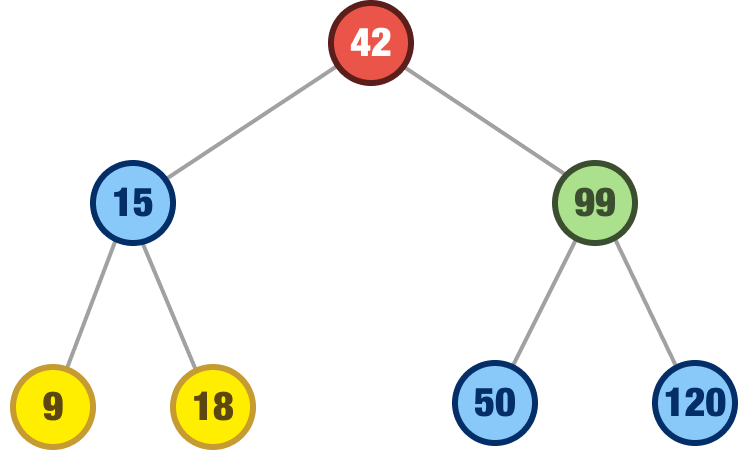
We are now at the last case. What happens when we remove a node that happens to have two children. Take a look at the following example where we wish to remove the 99 node:
When removing a node with two children, we can’t just pick one of the children nodes and call it a successful operation. If we do that, we may find that our tree is no longer valid. Some of the nodes may find themselves in the wrong places.
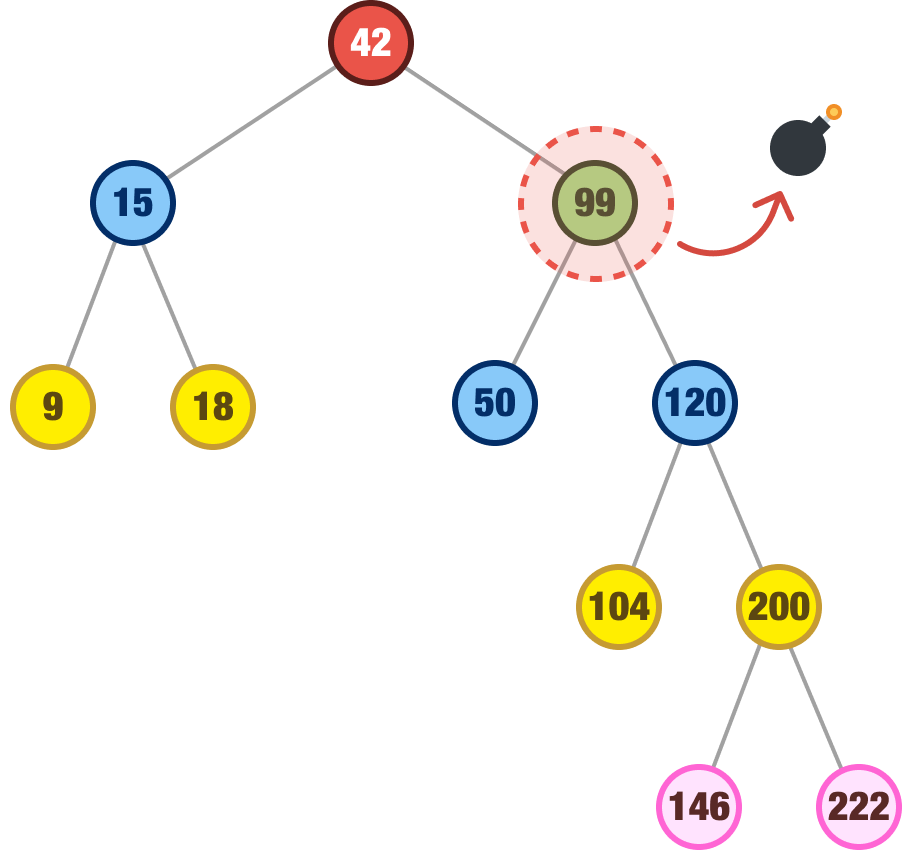
What we do in this case is look for the node with the next highest value, also known as the inorder successor, and we look for this node in the right subtree. For our situation where we are removing our node with a value of 99, the right subtree is the following:
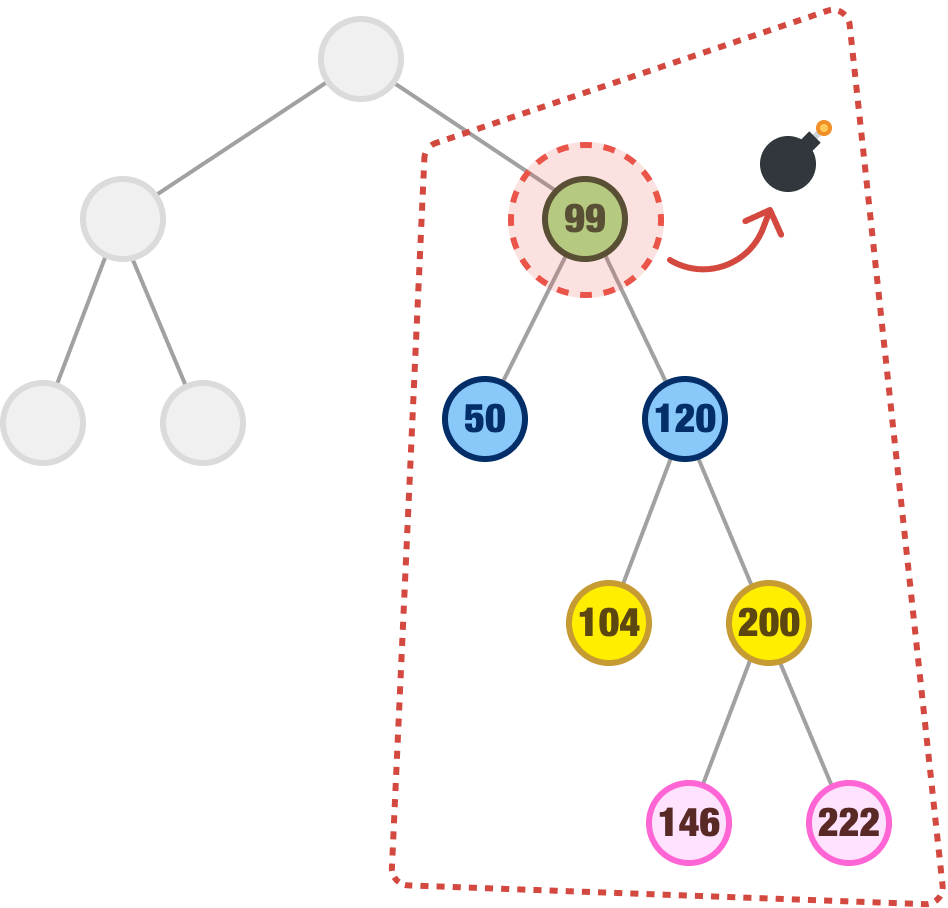
Which node in our subtree has the next highest value from 99? To describe the same thing differently, when we look at all the children to the right of our 99 node, which node has the smallest value? The answer to both of these questions is the node whose value is 104. What we do next is remove our 99 node and replace it with our 104 node:
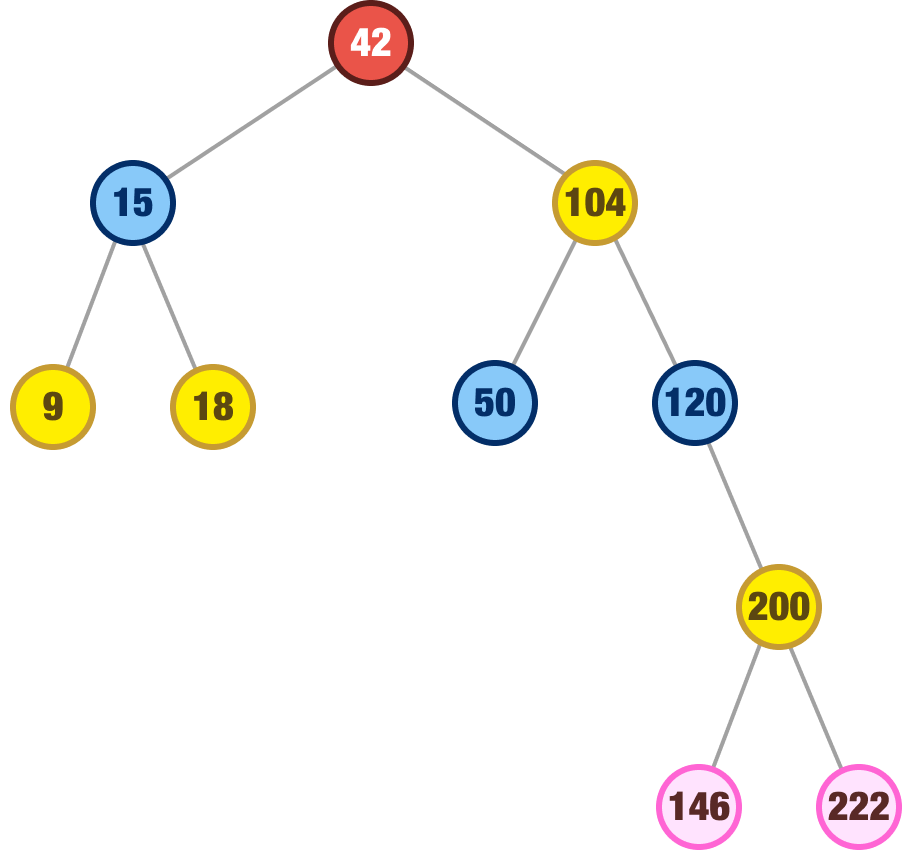
When we look at our binary search tree after this removal and swap, the integrity of all of the nodes is maintained. This isn’t an accident, of course. The inorder successor node will always have a value that ensures it can be safely plopped into the place of the node we are removing. That was the case with our 104 node that took over for our 99 node. That will be the case for other nodes we wish to remove as well.
If we had to summarize all of the words and diagrams into a few simple rules for adding and removing nodes, it would be the following:
For adding nodes:
For removing nodes:
Go through the above steps and make sure nothing sounds too surprising. They are almost the TL;DR version of what we saw in the previous sections. Our code is mostly going to mimic the above steps. In fact, let's look at our code now!
Our binary search tree implementation is made up of our familiar Node class and the BinarySearchTree class:
class Node {
constructor(data) {
this.data = data;
this.left = null;
this.right = null;
}
}
class BinarySearchTree {
constructor() {
this.root = null;
}
insert(value) {
// Create a new node with the given value
const newNode = new Node(value);
// If the tree is empty, the new node becomes the root
if (this.root === null) {
this.root = newNode;
return this;
}
// Traverse the tree to find the correct position for the new node
let currentNode = this.root;
while (true) {
if (value === currentNode.data) {
// If the value already exists in the tree, return undefined
return undefined;
} else if (value < currentNode.data) {
// If the value is less than the current node's value, go left
if (currentNode.left === null) {
// If the left child is null, the new node becomes the left child
currentNode.left = newNode;
return this;
}
currentNode = currentNode.left;
} else {
// If the value is greater than the current node's value, go right
if (currentNode.right === null) {
// If the right child is null, the new node becomes the right child
currentNode.right = newNode;
return this;
}
currentNode = currentNode.right;
}
}
}
remove(value) {
// Start at the root of the tree
let currentNode = this.root;
let parentNode = null;
// Traverse down the tree to find the node to remove
while (currentNode !== null) {
if (value === currentNode.data) {
// If we found the node to remove, proceed with removal process
if (currentNode.left === null && currentNode.right === null) {
// Case 1: Node has no children
if (parentNode === null) {
// If the node is the root of the tree
this.root = null;
} else {
// If the node is not the root of the tree
if (parentNode.left === currentNode) {
parentNode.left = null;
} else {
parentNode.right = null;
}
}
return true;
} else if (currentNode.left !== null && currentNode.right === null) {
// Case 2: Node has one child (left child only)
if (parentNode === null) {
// If the node is the root of the tree
this.root = currentNode.left;
} else {
// If the node is not the root of the tree
if (parentNode.left === currentNode) {
parentNode.left = currentNode.left;
} else {
parentNode.right = currentNode.left;
}
}
return true;
} else if (currentNode.left === null && currentNode.right !== null) {
// Case 2: Node has one child (right child only)
if (parentNode === null) {
// If the node is the root of the tree
this.root = currentNode.right;
} else {
// If the node is not the root of the tree
if (parentNode.left === currentNode) {
parentNode.left = currentNode.right;
} else {
parentNode.right = currentNode.right;
}
}
return true;
} else {
// Case 3: Node has two children
// Find the inorder successor of the node to remove
let successor = currentNode.right;
let successorParent = currentNode;
while (successor.left !== null) {
successorParent = successor;
successor = successor.left;
}
// Replace the node to remove with the inorder successor
if (successorParent.left === successor) {
successorParent.left = successor.right;
} else {
successorParent.right = successor.right;
}
currentNode.data = successor.data;
return true;
}
} else if (value < currentNode.data) {
// If the value we're looking for is less than the current node's value, go left
parentNode = currentNode;
currentNode = currentNode.left;
} else {
// If the value we're looking for is greater than the current node's value, go right
parentNode = currentNode;
currentNode = currentNode.right;
}
}
// If we reach this point, the value was not found in the tree
return false;
}
}Take a brief glance through the lines of code above. The comments call out important landmarks, especially as they relate to the binary search tree behavior we have been looking at. To see this code in action, here is an example:
let myBST = new BinarySearchTree();
myBST.insert(10);
myBST.insert(5);
myBST.insert(15);
myBST.insert(3);
myBST.insert(7);
myBST.insert(13);
myBST.insert(18);
myBST.insert(20);
myBST.insert(12);
myBST.insert(14);
myBST.insert(19);
myBST.insert(30);We are creating a new binary search tree and adding some nodes to it. This tree will look like the following:
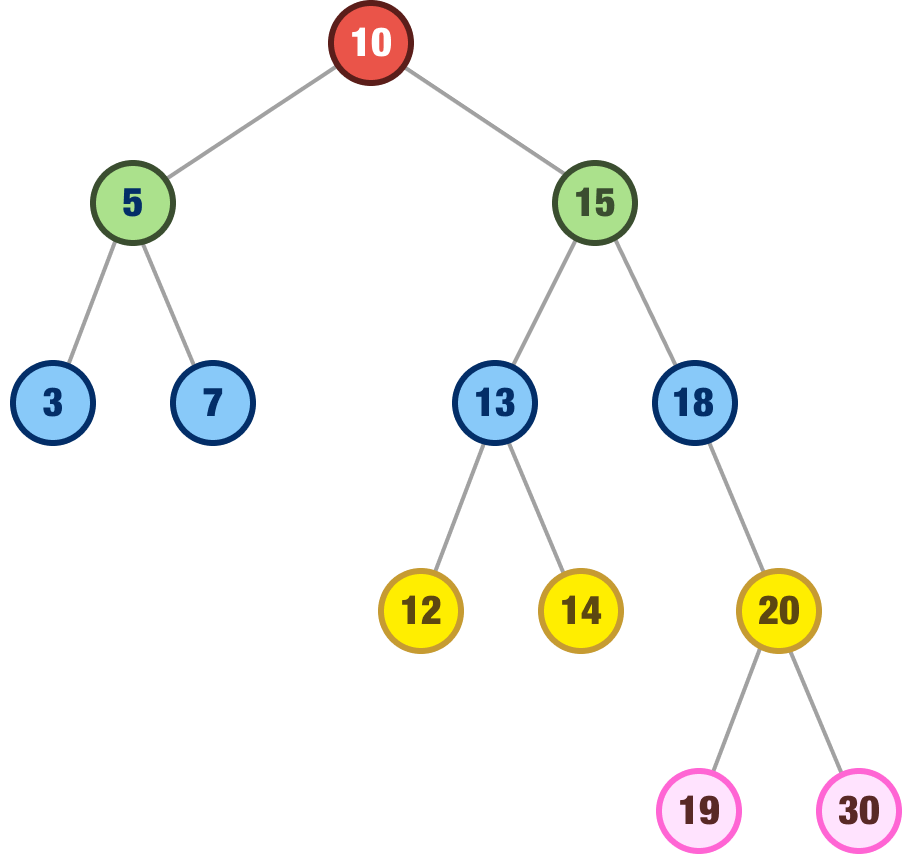
Let's say that we want to remove the 15 node:
myBST.remove(15);Our tree will rearrange itself to look as follows:
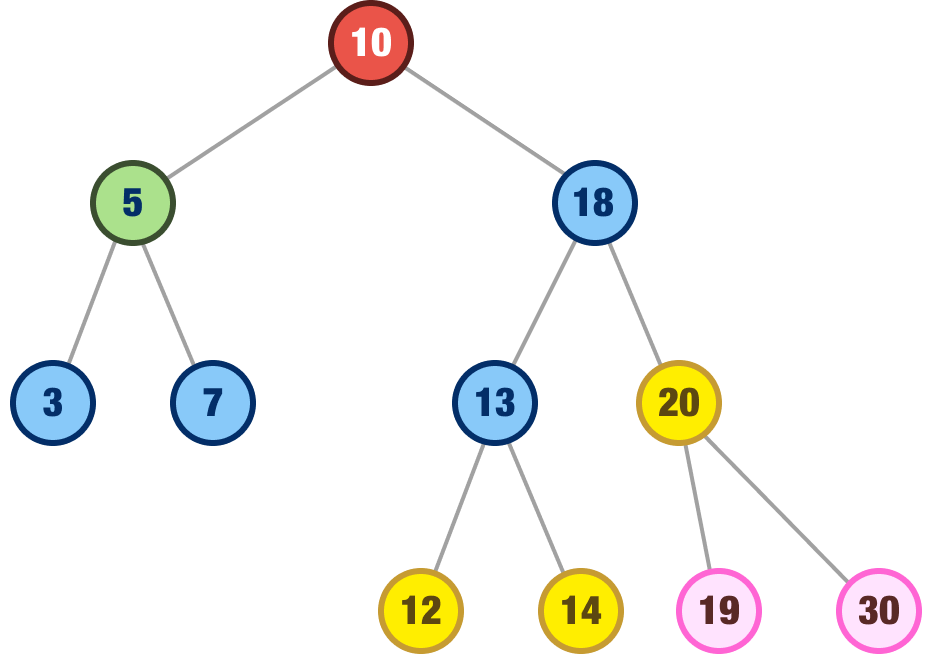
The 15 node is gone, but the 18 node takes its place as the rightful inorder successor. Feel free to play with more node additions and removals to see how things will look. To easily see how all of the nodes are related to each other, the easiest way is to inspect your binary search tree in the Console and expand each left and right node until you have a good idea of how things shape up:
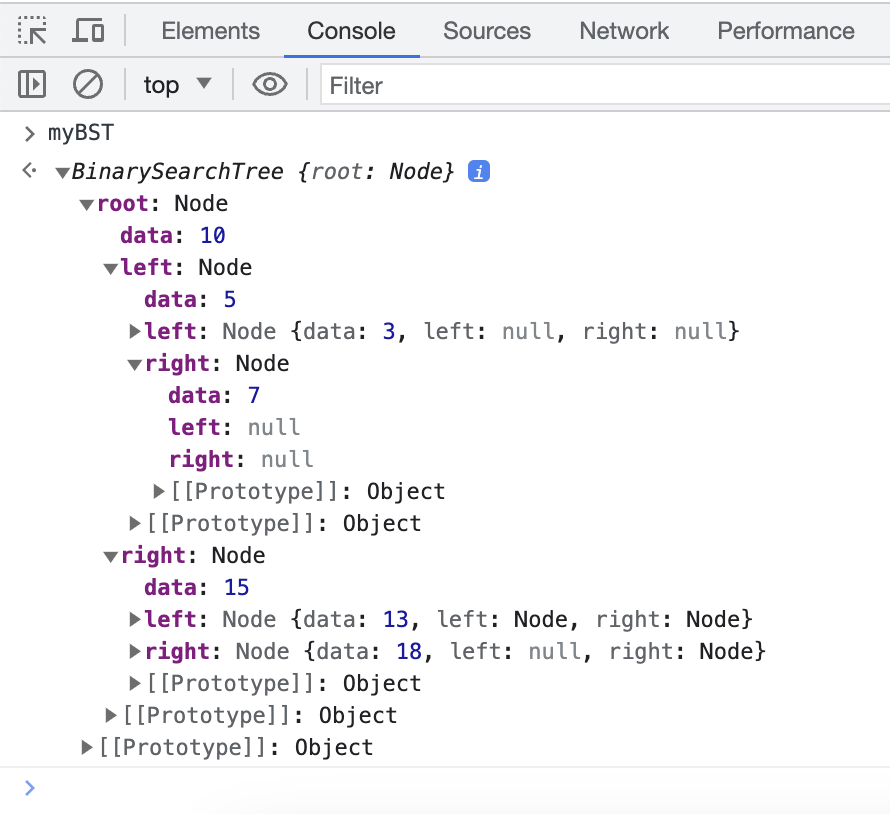
If you want to go above and beyond, you can create a method that will print an ASCII-art representation of a tree in our console, so do let me know if you have already done something like that.
The performance of our binary search tree is related to how balanced or unbalanced the tree is. In a perfectly balanced tree, the common operations like searching, inserting, and deleting nodes will take O(log n) time:
This is because we can avoid taking very uniquely long paths to find any single node. The worst case scenario is when our tree is heavily unbalanced:
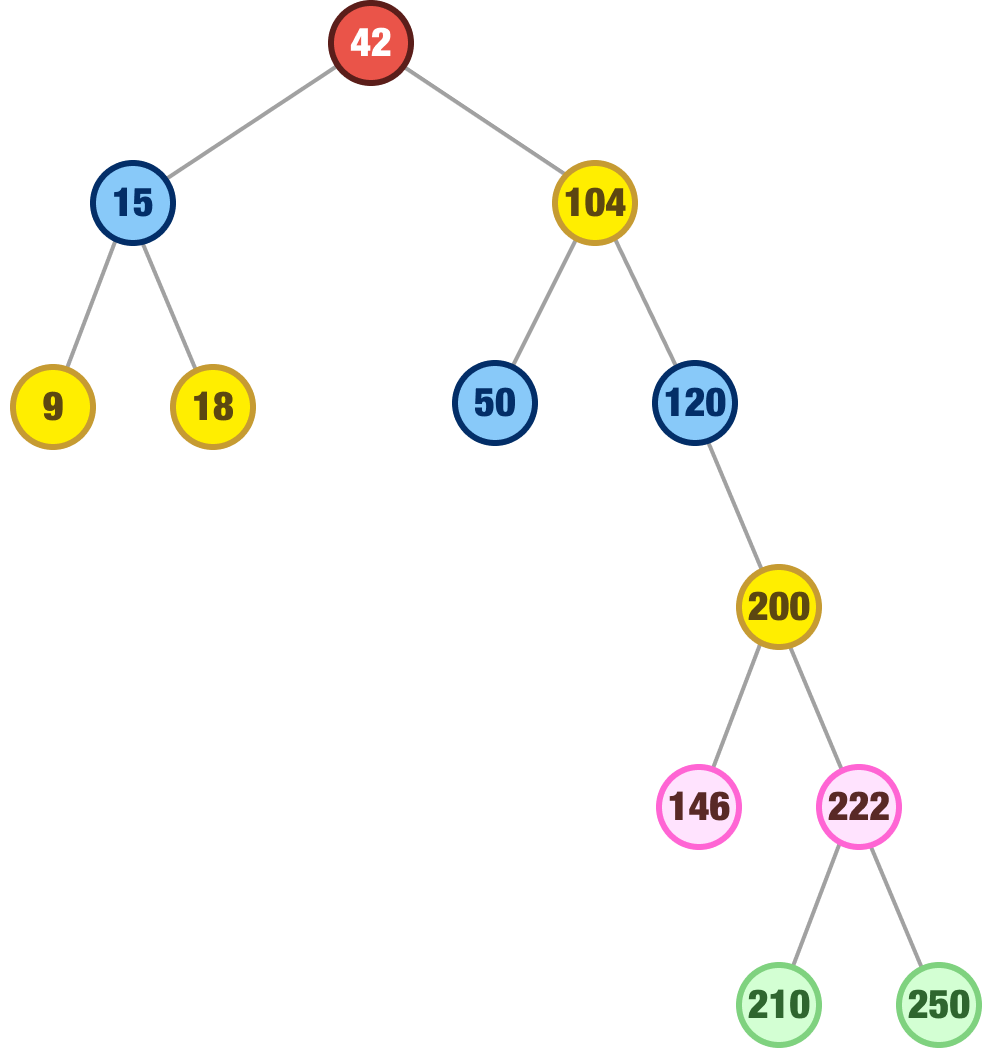
In this tree, if our node happens to be deep in the right subtree, we'll be exploring a lot of nodes relative to the total number of nodes in a tree. This gets us closer to a running time of O(n), which is the worst-case scenario.
As for the amount of memory a binary search tree takes up, that doesn't depend on how balanced or unbalanced our tree is. It is always O(n) where each node takes up a fixed amount of memory.
Binary search trees are pretty sweet. They are a type of binary tree with some added constraints to make them more suited for heavy-duty data wrangling. The constraints are to ensure the left child is always smaller than the parent and the right child is always greater. There are a few more rules around how nodes should arrange and re-arrange themselves when they get added or removed.
This type of structure allows us to efficiently search, insert, and delete operations in O(log n) time complexity, making binary search trees a popular data structure. However, as we saw a few moments ago, the performance of a binary search tree can be impacted by its balancedness. For heavily unbalanced trees, this can lead to worst-case scenarios with the time complexity of O(n). We'll look into how to force trees to be balanced in the future.
Just a final word before we wrap up. If you have a question and/or want to be part of a friendly, collaborative community of over 220k other developers like yourself, post on the forums for a quick response!
