Learn how the Sieve of Eratosthenes algorithm finds prime numbers using a simple sifting technique, similar to a kitchen sieve. Includes step-by-step visualization, JavaScript implementation, and beginner-friendly explanation of this ancient yet powerful mathematical method.

What does your common kitchen sieve have in common with finding prime numbers?

What if a geographer and mathematician named Eratosthenes (also known as Pentathlos by his homies!) is thrown into the mix? Well, we are about to find out!

A problem that lives rent-free in the heads of many mathematicians revolves around determining whether a number is prime or not. For a quick recap, a prime number is a number that has exactly two factors: 1 and itself. For example, 7 is prime because you can only create it by multiplying 1 × 7. But 12 isn't prime because it can be created in a few ways: 1 × 12, 2 × 6, or 3 × 4. Numbers that aren't prime are called composite numbers.

Now, finding prime numbers might sound simple—just test if a number can be divided by anything else, right? But there's a catch. As numbers get larger, this becomes incredibly time-consuming. Let's say we want to test whether 997 is prime. We'll need to try dividing it by every number up to its square root (about 31 divisions) to be sure. Now imagine testing a number with hundreds of digits!

This challenge has fascinated mathematicians for a bazillion years because:

• There's no simple formula to generate prime numbers
• Prime numbers become increasingly sparse as numbers get larger
• There are infinitely many prime numbers (as proven by Euclid)
• Testing very large numbers for primality is very important for modern cryptography, so this isn’t just a theoretical exercise

This is where something known as the Sieve of Eratosthenes comes in. The Sieve of Eratothesenes (try saying that five times fast!) is an algorithm for finding all prime numbers up to a limit we specify. Let’s dive into all of this in the following sections.

Onwards!

A Walkthrough

A critical detail in understanding how the Sieve of Eratothesenes works lies in the use of the word Sieve. If you are not familiar with what a sieve does, think of it as a large colander (or sifter) where smaller particles pass through, but larger particles get caught:

For example, if we pour some coarse liquid into a sieve, the liquid and small particles will fall through while the larger pieces will get caught. The Sieve of Eratosthenes works in a similar way—but instead of separating solids from liquids, it filters out composite numbers to leave prime numbers behind.

Let’s say that our goal is to find all prime numbers less than the target number of 100. To help us visualize our starting point, here is a grid of numbers going from 1 to 100:

Our goal is to cross out all of the composite numbers. The numbers that are not crossed out will be the prime numbers.

Let’s start with the number 1. As it turns out, number 1 is special. It is neither prime nor composite, so we can cross that out and jump right on over to number 2:

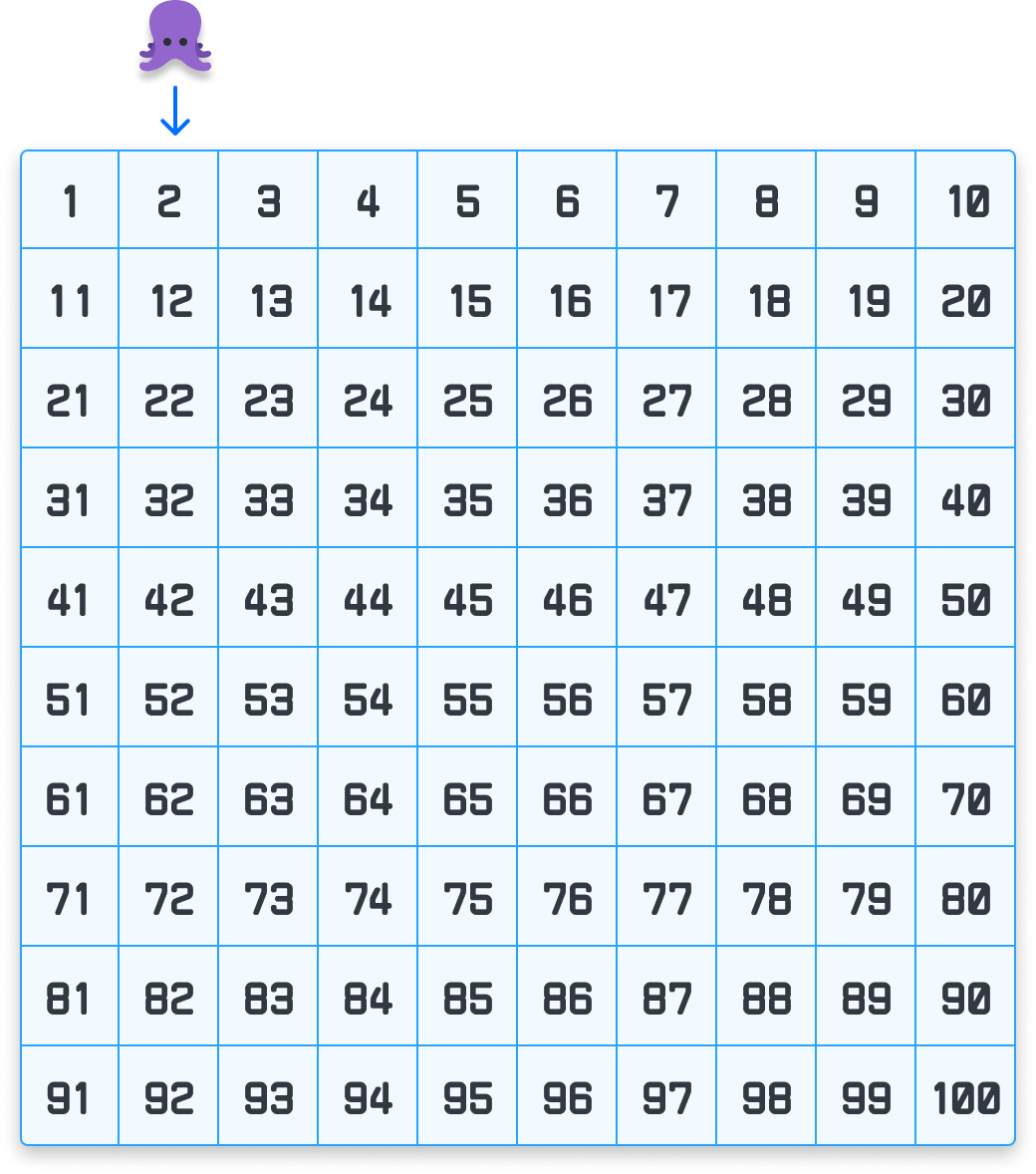
At this point, we are going to cross out every multiple of 2:

We eliminated all even numbers except for number 2 itself, for 2 is a prime number. Now, we shift our attention to the next uncrossed item in our grid. That would be the number 3, and we cross out every item that is a multiple of 3:

Note that some numbers that are multiples of 3 have already been crossed from an earlier step where we crossed out all numbers that are multiples of 2. That is to be expected and collisions like this will only increase as we keep moving through. Next, we move to our next uncrossed number, and that number is 5. We skip over 4 because we already crossed it out earlier. At 5, we repeat the same steps where every multiple of itself is crossed out:

With the exception of 5 itself, all numbers ending in 5 and 0 are now crossed out. Our next number is 7, and all multiples of 7 will get crossed out:

At what point do we stop going to the next uncrossed number and checking off multiples of itself? We stop checking when we reach the square root of our target number, which is 100. The next uncrossed number is 11, but 11 is greater than the square root of 100, which is 10. We can see why that is the case. If we start crossing out multiples of 11, after 11 itself, the next number is 121 (11 x 11), which goes beyond the range defined by our target number.

All of the uncrossed numbers we see right now must be prime numbers:

The list of prime numbers less than our target of 100 are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97. By using the Sieve of Eratosthenes, we were able to find them by using a simple algorithm that filters out all of the composite numbers in our range. Speaking of the algorithm...

Algorithm Summarized

In the previous section, we walked through an example where we used the Sieve of Eratosthenes to find all the prime numbers less than our target value of 100. If we had to summarize our algorithm with an eye towards implementing this in code, it would be as follows:

1. Create a list: Start by creating a list (or array) of boolean values, indexed from 0 to the target value of n. Each index represents whether the number is prime.
   
   This is similar to us using a grid earlier, but we are now switching to using a linear data structure:

2. Set default list value: For our list, initialize all values as true. The true value indicates that these values will be prime.
   
   This also means that all non-prime values will eventually be marked false, but we can get a head start and mark 0 and 1 as false now itself.

3. Start with the First Prime: Begin with the smallest prime number, which is 2.
4. Mark Multiples as Non-Prime: For the current number (starting with 2), mark all of its multiples as false in the list. The False value indicates these values are not prime. This is the equivalent of crossing out values from our example in the previous section.
5. Move to the Next Unmarked Number: Find the next number in the list that is still True (indicating it is prime) and repeat step 4.
6. Stop Condition: Stop the process once we’ve reached the square root of n, for all non-prime numbers will have been marked by this point.
7. Collect Primes: At this point, the indices that remain True must be prime numbers.

The biggest difference in our algorithm vs. the example we saw earlier is the use of a list. The list and its index positions (from 0 to n) are the equivalent of our grid of values. Setting each value to true or false is equivalent to us crossing out values that are no longer prime.

The JavaScript Code

Before we call it a day, let’s look at what the JavaScript equivalent of the above algorithm looks like. Behold, the sieveOfEratosthenes function:

function sieveOfEratosthenes(n) {
  // Create a boolean array "prime[0..n]" and initialize
  // all entries it as true. A value in prime[i] will
  // finally be false if i is Not a prime, true otherwise.
  let prime = Array(n + 1).fill(true);
  
  prime[0] = prime[1] = false; // 0 and 1 are not prime numbers

  for (let p = 2; p * p <= n; p++) {
    // If prime[p] is not changed, then it is a prime
    if (prime[p] === true) {
      // Update all multiples of p to false indicating not prime
      for (let i = p * p; i <= n; i += p) {
        prime[i] = false;
      }
    }
  }

  // Collecting all prime numbers
  let primes = [];
  for (let i = 2; i <= n; i++) {
    if (prime[i]) {
      primes.push(i);
    }
  }

  return primes;
}

To use this function, we need to define a target value and call sieveOfEratosthenes with that value passed in as an argument:

const n = 300;
const primesUpToN = sieveOfEratosthenes(n);
console.log(`Prime numbers up to ${n}:`, primesUpToN);

When this code runs, all of the prime numbers up to the target value of 300 will be printed. That's a pretty large list, but you can see the full source code and try this for yourself by going here.

Runtime and Memory Complexity

The Sieve of Eratosthenes algorithm is fairly efficient - both in runtime and memory complexity. Let's walk through how it is able to pull this off.

Runtime Complexity

From a runtime point of view, this algorithm has a runtime complexity of O(n * log log n). This can look a bit confusing, but let's break it down step-by-step:

1. The outer loop of the algorithm runs from 2 to the square root of the target number n. This means the outer loop will run approximately square root of n (aka √n) times.
2. Inside the outer loop, for each number p that is not crossed out yet (i.e., it's a prime number), we need to cross out all the multiples of p that are less than or equal to n.
3. The number of multiples of p that are less than or equal to n is approximately n/p. So, the inner loop will run n/p times for each prime number p.
4. Now, the really REALLY important detail is that the sum of all these fractions (1/2 + 1/3 + 1/5 + 1/7 + ...) is approximately equal to log log n. This is a slowly growing function, which means the total number of operations is O(n * log log n).

Now, Step IV earlier is where things may get a little confusing. How did we go from a sum of those fractions to the complicated log-based runtime? It has to do with what the sum (1/2 + 1/3 + 1/5 + 1/7 + ...) represents. This sum is a variation of the harmonic series:

It is a variation because of three things that make it different from the standard harmonic series:

1. We're only summing over prime numbers (not all integers)
2. We're multiplying by n
3. We only go up to √n

This total summation can be captured by the special mathematical function called the logarithm function whose formuala looks as follows:

sum = ln(ln(n)) + γ + O(1/ln(n))

Where:

• ln() is the natural logarithm function
• γ (gamma) is the Euler–Mascheroni constant, which is approximately 0.577215664901532860606512090082

If we break this down even further:

1. The term ln(ln(n)) is the key part of the formula. The natural logarithm of the natural logarithm of the number n is a slowly growing function. This is where the "log log n" part of the runtime complexity comes from.
2. The + γ term is a constant that's added to the sum. The Euler–Mascheroni constant is a mathematical constant that arises in this context.
3. The O(1/ln(n)) term is a small correction factor that becomes negligible as n gets larger. Because of how Big-O notation works, we can ignore values that aren't the biggest contributor to the overall complexity.

So, the overall sum of those fractions grows approximately as ln(ln(n)), which is a very slowly growing function. This is what makes the Sieve of Eratosthenes algorithm so efficient, especially for large values of n.

Memory Complexity (Space Complexity):

The memory complexity of the Sieve of Eratosthenes algorithm is O(n). This means that the amount of memory the algorithm needs to use grows linearly with the size of the input n.

Specifically, as we described earlier, the algorithm needs to store a boolean (true / false) value for each number from 2 to n, indicating whether that number is prime or not. This requires an array of size n+1 (since we start counting from 0):

 

There are variations of the algorithm that are more space efficient. For example, the memory usage can be optimized further by using a bit array instead of a boolean array, which can reduce the memory usage by a factor of 8. There are also other optimization techniques, like the Segmented Sieve or Wheel Factorization, that can help reduce the memory usage for larger values of n, but I'll leave it up to you to see if those optimizations are going to be important for your use cases.

Conclusion

Wrapping this all up, the Sieve of Eratosthenes is a powerful and efficient algorithm for finding all prime numbers up to a given limit. By using a simple and repetitive approach to mark the multiples of each prime, starting from 2, the algorithm quickly identifies all non-prime numbers, leaving only the prime numbers behind.

Also on a completely unrelated note, doesn’t all this talk of prime numbers remind you of one of the greatest fighting arcade games of all time, Primal Rage?

This game is like Mortal Kombat but uses dinosaurs and other giant prehistoric animals. What’s not to like...with the exception of maybe the strange bugs and glitches in the console ports?

Just a final word before we wrap up. If you have a question and/or want to be part of a friendly, collaborative community of over 220k other developers like yourself, post on the forums for a quick response!