A Bloom filter is a popular probabilistic data structure that efficiently tests whether an item exists in a collection of data. Just based on this description, you and I may have a lot of questions. For example, don’t we already have data structures (such as hashtables) that can quickly tell us whether an item exists in a collection? In the context of getting a precise answer, what does probabilistic mean? Getting back to hashtables, can anything really be more efficient than its O(1) running time?

In this tutorial, we will not only answer questions like these, we'll dive deep into what Bloom filters are and what makes them extremely powerful.

Onwards!

What in the world is a Bloom filter?

To better understand what Bloom filters are and how they work, let’s start by looking at an example. Imagine we are a popular social network, and we have a registration form where a user can specify a username as part of creating their account:

When the user (or a very smart pet) specifies the username they want to use, we need to ensure the username is unique and not already used by someone else. If the username is unique, then the registration process can continue. If a specified username is already being used, we block registration until a valid username is provided:

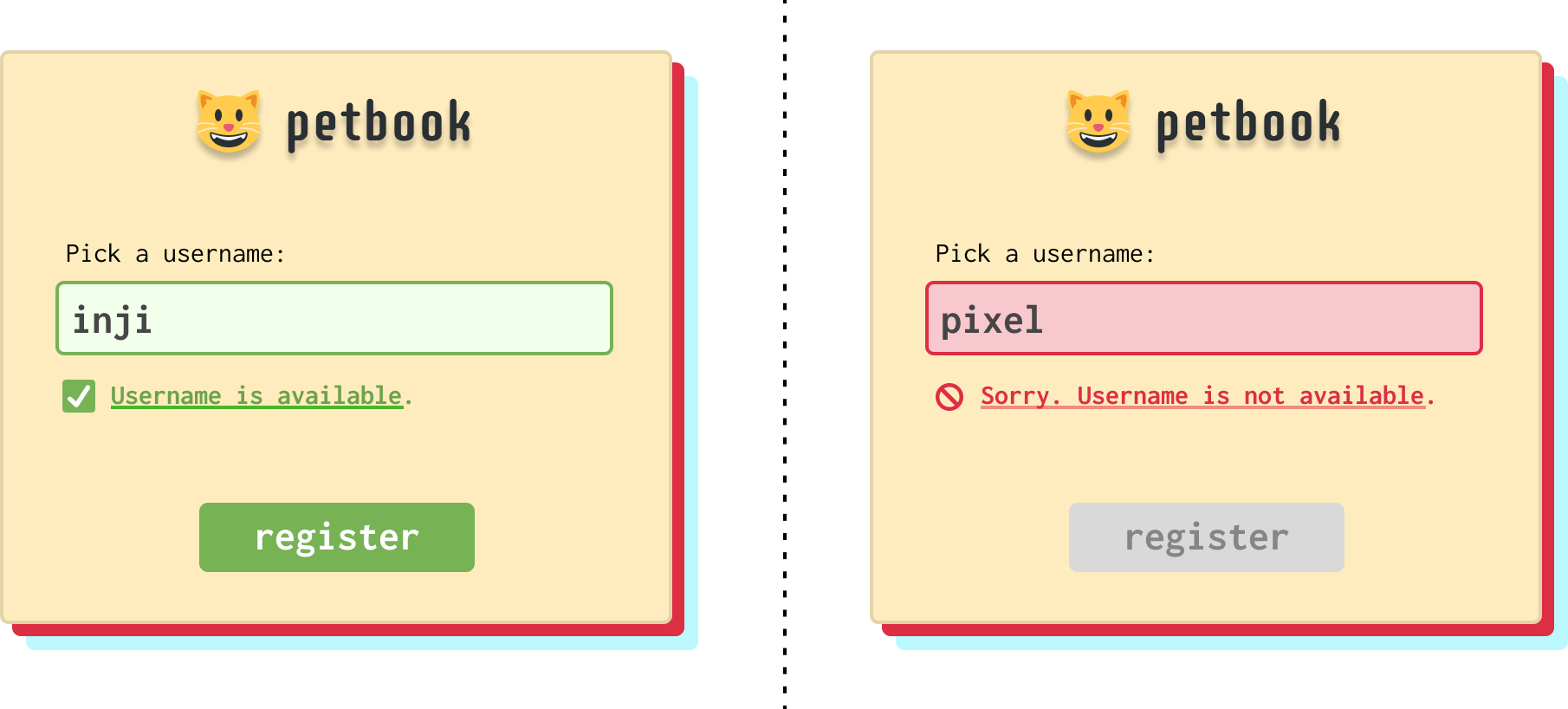
Behind the scenes, checking to see if a username is or isn’t available involves communicating with a database of usernames:

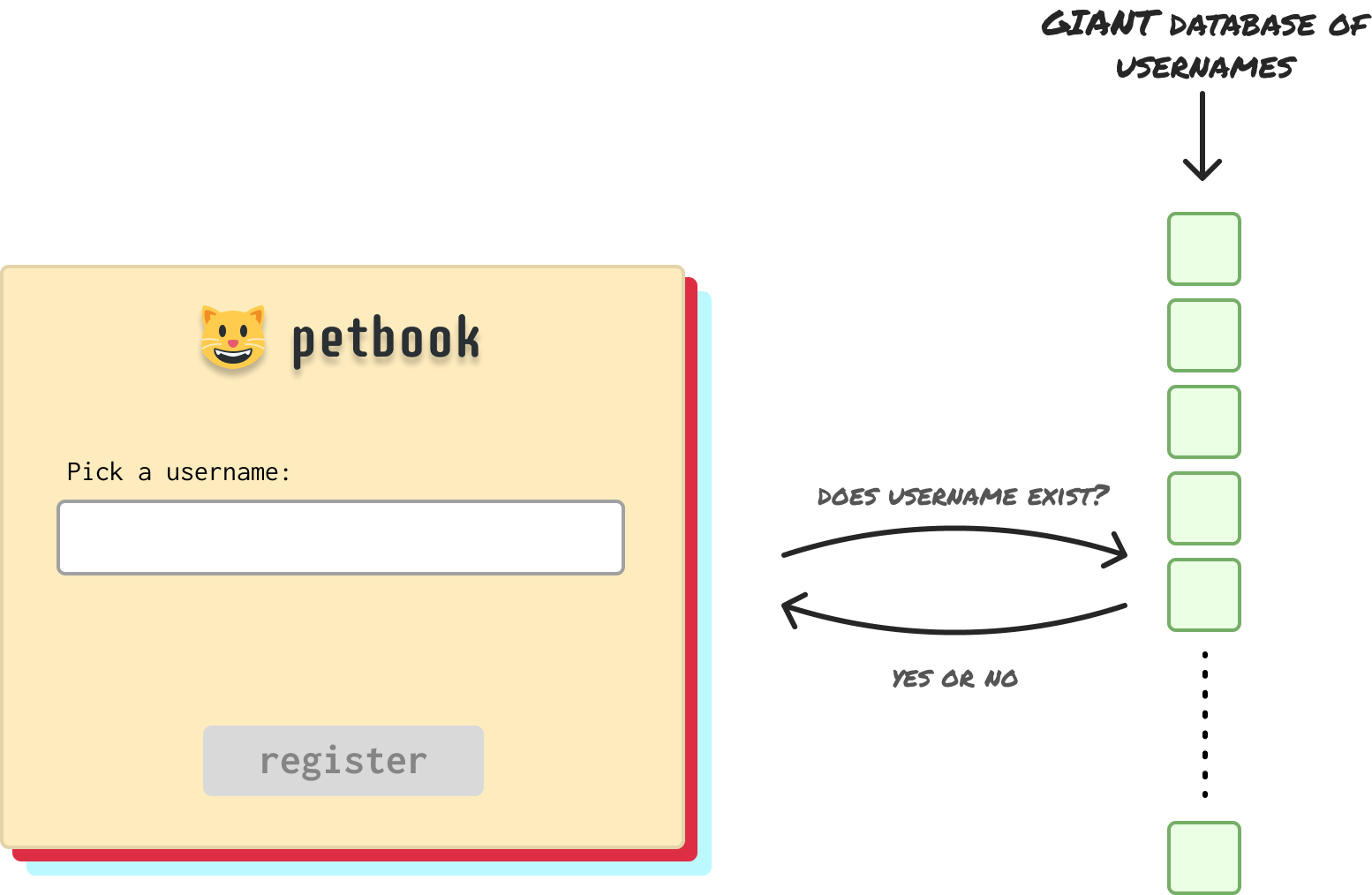
Because our social network is popular, the database containing our list of existing usernames is very VERY large. To not slow down the registration process, we need to ensure that our end-to-end story for checking a username is fast and accurate. To perform this check, in a world without Bloom filters, we have a few approaches we can take:

1. Scan all the entries in our database. This would be akin to using something like an Array and going item by item. As we can imagine, this isn’t great. This approach would be too time-consuming and run in O(n) time. Because databases are typically disk-based with slow read/write capabilities, this would be a slow O(n) in real-world time. Yikes!
2. Use something faster, like a hashtable, to give us a yes/no in O(1) time. This seems like a perfect solution, right? While a hashtable is extremely fast, the problem is that it is too memory-intensive when we have a lot of items. If we end up with collisions, which will happen with really large datasets, some of the O(1) speed advantages will also go out the window.

What we need is a fast and memory efficient solution to help us out here. What we need is the star of this tutorial, the Bloom filter. Think of a Bloom filter as an optimization layer that sits between our request and the database:

Whenever we need to check whether a username is in use or not, the goal is to have our really fast Bloom filter provide an answer. Only in a few specific cases should the slower database be consulted. How does our Bloom filter pull this off in a fast and memory/storage-efficient way? It has to do with what exactly is stored by our Bloom filter. The Bloom filter does not store the actual source data. It stores a fingerprint of the data in the form of a single 0 or a 1. That’s almost as lightweight of a value we can get. Let’s dive further into this.

Initial Setup

To start using a Bloom filter, we first need to set it up and populate it with the initial values. To pull this off, there are three things we will need:

1. The initial data
2. A bit array
3. A number of hash functions, each of which maps an element to an array position in the bit array

These three things seem a bit unrelated, but they will make more sense in a few moments.

Initial Data

First, we need some data. Let’s continue our example and go with a collection of usernames:

In practice, this list will be massive with millions (or even billion+) entries. For our explanation and the physical constraints of the page and screen size, we will keep it much smaller.

Bit Array

Next, we will need a bit array. If you aren’t familiar with bit arrays, they are nothing more than an array that only stores 0’s and 1’s as its value:

There are two details to note here:

1. When starting out, we will initialize our bit array with only 0 values.
2. The exact length of the bit array is a combination of how much data we have and how accurate our responses need to be. We’ll dive into this in a bit more detail later. For now, we’ll just go with an arbitrary size of 10 items that fits on the page.

Hash Functions

Lastly, we need a handful of hash functions:

What these hash functions do is map our username to an index position in our bit array. The exact number of hash functions, often represented as k, is something we can adjust based on how complex our data is and how much accuracy we want. This too is something we’ll dive into a bit later, but for our example, we’ll just use 2 hash functions.

Our entire setup for populating our Bloom filter looks as follows:

It's Example Time

The first item we want to store is the username inji. What we do is pass this value through our first hash function. Our hash function will return a value between 0 and 10 in our bit array, and let’s say it returns a 5. We will use this 5 to find the appropriate value in our bit array and set the value there from 0 to 1:

We repeat these steps, but we now go to the second hash function. This time, our second hash function returns a value of 7. We set the value at the 7th index position in our bit array to 1:

We are now done storing the username inji. In our Bloom filter, this username is now represented by a 1 at index positions 5 and 7. Let’s go a little faster. The next username we want to store is muffins. When we put this value through both of our hash functions, they will return a 0 and 6:

The bit array values at the 0th and 6th index position are now set to 1.

Moving right along, we have our username bluey. The result of running this value through our hash function is 3 and 4:

Our next username to pass to our Bloom filter is bingo. When we pass this value to both our hash functions, the index positions that are returned are 7 and 10:

Notice that our value at index position 7 was already set earlier when adding inji. That’s OK. There is nothing special we need to do here. We will just leave the value in our bit array as-is.

We are now at pixel, our final username. For this username, our hash functions return a value of 1 and 10:

At this point, we have all of our initial values represented in our bit array. What we did is take each item, pass it through both our hash functions, map the returned values to the appropriate position in the bit array, and ensure the bit array value at those positions is set to 1. From here on out, we can simplify our setup to just be our bit array and the hash functions:

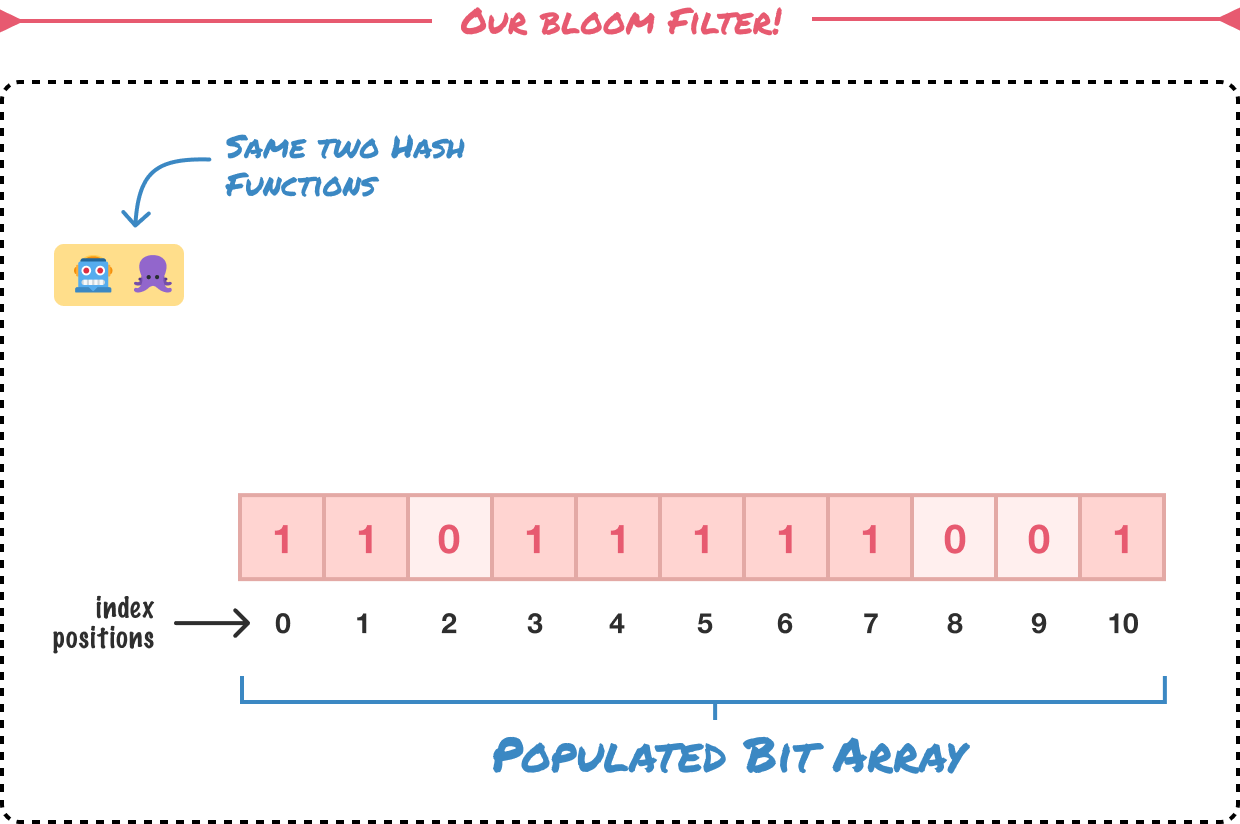
This combination of our bit array and hash functions makes up our...🥁...Bloom filter! All of the other information is no longer needed because our Bloom filter is now a lightweight representation of our initial data and its results.

Checking if a Value Exists

Now that we have our initial data represented in our Bloom filter, let’s use it to check whether a value exists in our Bloom filter or not. Let’s start by checking if the username scooby_doo exists. The first thing we do is pass this value to both of our hash functions. The values that get returned by them are 4 and 8:

What we do next is check the values at index positions 4 and 8 in our Bloom filter:

The value at index position 4 is 1. The value at index position 8 is 0. How should we interpret this result? Whenever the result of a hash function points to a value that is 0 in our bit array, the outcome is straightforward. The item we are checking for isn’t a part of the larger collection. We can say with 100% certainty that the username scooby_doo hasn’t already been registered, and our Bloom filter can do that directly without needing to consult the slower database:

It doesn't matter if our Bloom filter happens to use 99 hash functions, and just 1 of those 99 hash functions returns a 0. The item is considered to not exist. Every single hash function must return a result that points to a 1 for us to consider the item as being a part of the larger collection.

Speaking of...let’s say we want to check if the username muffins exists. What we do is similar to what we did before. We pass this value to both of our hash functions:

What values do we think will get returned? If we recall from a few steps earlier in the previous section, muffins was one of the initial username values we had already passed into our hash functions for representation in our bit array. The returned values then were 0 and 6. Because our hash functions won’t change the output for the same input, the returned values now will also still be 0 and 6. We map these values to the appropriate location in our bit array:

What we see is a value of 1 set at index positions 0 and 6. When we see a 1 for all of our hash functions, what do you think our answer is going to be? Is muffins a part of our usernames database?

It seems reasonable to say that the answer is going to be a yes. This turns out not to be the case, and the reason behind it is where the probabilistic nature of Bloom filters comes in:

The answer in this situation is more of a yes-ish. Me saying yes-ish isn’t a typo or me sneezing mid-sentence. It is a part of how Bloom filters work where they can’t say with 100% certainty whether something we are looking for exists. The best they can do is give a high-confidence answer that the item does exist, but we will need to check the actual source to be 100% certain. This can all be visualized as follows:

We have to do this because Bloom filters are prone to generating false positives where they may say an item exists, whereas, in reality, it doesn't. This happens when an element that was never added to the Bloom filter hashes to bit positions that were all previously set to 1 by other elements. For the username muffins, this turned out to not be a false positive. This username does, in fact, exist in our larger database. That won’t be the case for our next username. Spoiler alert.

Let’s say we want to check whether the username rusty is available for registration. When we send it through to both our hash functions, we get the results 1 and 5:

The locations 1 and 5 in our bit array stores a 1. What we do not know is what username value (or values) may have been involved in setting the bit array value to 1 at these two positions. It could have been rusty. It could have been some other username like inji or pixel. Because we don’t know for certain and the initial logic for which elements flipped the bits in the first place is long lost, we have to perform the slower check in our actual database to verify:

In this case, it’s a good thing we did because rusty seemed to be positive according to our Bloom filter, but it was actually not in the database at all. This is an example of a false positive.

Optimizing our Bloom Filter

At this point, you and I should have a good high-level understanding of how a Bloom filter works and the situations in which it will return a definitive no and a probabilistic yes. Now that we’ve gotten this far, it’s time to go even deeper and look at how a Bloom filter works in real-life scenarios. As you can imagine, our example Bloom filter with its initial data set of 5 items and 2 hash functions is not how most Bloom filters in production-grade environments are set up.

With Bloom filters, there are three values we can adjust:

1. The length of our bit array, represented as an m
2. The number of hash functions, represented as k
3. The false positive rate, represented as p

Combinations of these values will determine how accurate our Bloom filter is, how fast it returns an answer, and how much memory it takes. There is also the value n that represents the number of elements our Bloom filter will need to provide a representation for, but we will rarely adjust this. Usually, we will have our Bloom filter operate on our full dataset.

Optimal Bit Array Size (m)

The optimal bit array size can be calculated by the following formula:

One of the biggest deciders of the bit size is p, the false positive probability value. This value is in the range of 0 < p < 1. It must be greater than 0, for it is impossible to have zero false positives in a Bloom filter with finite space. The value must also be less than 1, for a value of 1 would mean every query returns as positive.

In most cases:

• Values typically range from 0.001 (0.1%) to 0.1 (10%)
• 0.01 (1%) is a commonly chosen value that balances space efficiency and accuracy
• Lower values (closer to 0) provide better accuracy but require more space
• Higher values (closer to 1) save space but increase the chance of false positives

 

Optimal Number of Hash Functions (k)

The optimal number of hash functions can be calculated as:

This formula balances two competing factors:

1. Too few hash functions: The bit array will be under-utilized, leading to higher false positive rates because fewer distinct bits are set per element. This makes it more likely that the specific combination of bits needed to test whether an element exists are not will coincidentally all be set by other elements.
2. Too many hash functions: The bit array becomes saturated too quickly, again increasing the probability of collisions and false positives. This also slows down operations as each lookup requires computing more hash functions.

When optimally chosen, k minimizes the false positive probability for a given bit array size and element count. For most practical applications, the optimal k typically falls between 3 and 10.

Putting it All Together

Let’s say that our database of usernames has 10 million entries (n). We want to use a Bloom filter to quickly see if a username we are checking for already exists or not, and we have a target false probability rate (p) of 1% or 0.01.

The optimal bit array size (m) can be calculated as follows:

Therefore, for our 10 million usernames with a false probability rate of 1%, the optimal bit array size should be approximately 95.85 million bits. From here, we can then calculate the number of hash functions we will need:

The optimal number of hash functions (k) we will need for our bit array size (m) and number of elements is 7.

 

Performance Characteristics

From the previous section, we sorta kinda get the idea that the Bloom filter is a pretty efficient data structure provided we are willing to sacrifice a bit of certainty with our false positive probability. The following table provides a summary of its performance characteristics:

Action	Best	Average	Worst
Insertion	O(k)	O(k)	O(k)
Query (Check)	O(k)	O(k)	O(k)

Across the common insertion and query operations, the running time is always O(k). The reason is because we will have k hash functions and each hash function will run in O(1) time. This means the running time is O(k * 1) or just O(k).

Now, the thing to recognize is that focusing on just the Bloom filter’s performance doesn’t paint the full picture:

Whenever the answer isn’t a definitive No, we will have to talk to our database-like structure for a seeking operation which can significantly increase the total running time:

We can approximate the total running time by also looking at how long a database lookup will take. As with any database, there are three performance ranges for this looking-up operation:

1. Hash Table Lookup → O(1)
2. Index Search (B-Tree, etc.) → O(log⁡N)
3. Full Table Scan (worst scenario) → O(N)

Add in some good old-fashioned disk and network latency, and we should recognize that the bigger performance picture with Bloom filter is only O(k) when the Bloom filter can quickly (and with certainty) return a no answer. The moment the Bloom filter has to go talk to the database, the real-world time will be much greater.

 

Simple Bloom Filter Implementation

Before we wrap up and call it a day, let’s look at a simple implementation of a Bloom filter. If you want to try this out on your own, create a new HTML document and add all of the following content into it by either manually entering it or by copying/pasting it from this file on Github:

<!DOCTYPE html>
<html>
  <head>
    <title>Bloom Filter Example</title>
  </head>
  <body>
    <script>
      class BloomFilter {
        /**
         * Constructor for the Bloom Filter.
         * @param {number} size - The size of the bit array.
         * @param {number} numHashFunctions - The number of hash functions to use.
         */
        constructor(size, numHashFunctions) {
          // Store the size of the bit array.
          this.size = size;
          // Initialize the bit array with 0s.
          this.bitArray = new Array(size).fill(0);
          // Store the number of hash functions.
          this.numHashFunctions = numHashFunctions;
        }

        /**
         * Adds an element to the Bloom Filter.
         * @param {string} element - The element to add.
         */
        add(element) {
          // Loop through the number of hash functions.
          for (let i = 0; i < this.numHashFunctions; i++) {
            // Calculate the index using a hash function.
            const index = this.hash(element, i) % this.size;
            // Set the bit at the calculated index to 1.
            this.bitArray[index] = 1;
          }
        }

        /**
         * Checks if an element might be in the Bloom Filter.
         * @param {string} element - The element to check.
         * @returns {boolean} - True if the element might be present, false if definitely not.
         */
        contains(element) {
          // Loop through the number of hash functions.
          for (let i = 0; i < this.numHashFunctions; i++) {
            // Calculate the index using a hash function.
            const index = this.hash(element, i) % this.size;
            // If any bit is 0, the element is definitely not present.
            if (this.bitArray[index] === 0) {
              return false;
            }
          }
          // All bits are 1, so the element might be present.
          return true;
        }

        /**
         * A simple hash function.
         * @param {string} element - The element to hash.
         * @param {number} seed - A seed to generate different hash values.
         * @returns {number} - The hash value.
         */
        hash(element, seed) {
          // Initialize the hash value.
          let hash = 0;
          // Combine the element and seed.
          const str = element + seed;
          // Loop through the characters of the combined string.
          for (let i = 0; i < str.length; i++) {
            // Get the ASCII code of the character.
            const char = str.charCodeAt(i);
            // Shift and add to generate a hash.
            hash = (hash << 5) - hash + char;
            // Convert to 32bit integer.
            hash = hash & hash;
          }
          // Return the absolute hash value.
          return Math.abs(hash);
        }
      }

      // Example Usage
      // Size of the bit array.
      const filterSize = 100;
      // Number of hash functions.
      const numHashes = 3;
      // Create a Bloom Filter instance.
      const bloomFilter = new BloomFilter(filterSize, numHashes);

      // Sample data to add to the filter.
      const sampleData = ["apple", "banana", "cherry", "date"];
      // Add each item to the filter.
      sampleData.forEach((item) => bloomFilter.add(item));

      // Test elements to check.
      const testElements = ["apple", "grape", "cherry", "kiwi"];
      // Loop through the test elements and check their presence.
      testElements.forEach((element) => {
        // Check if the element might be present.
        if (bloomFilter.contains(element)) {
          // Print the result to the console.
          console.log(`"${element}" might be present.`);
        } else {
          // Print the result to the console.
          console.log(`"${element}" is definitely not present.`);
        }
      });
    </script>
  </body>
</html>

What we have here is both a simple implementation of a Bloom Filter and some sample code that puts our Bloom filter through its paces:

The comments in the code explain what the major parts of our code do. The code is designed to mimic the explanation we have seen here on how Bloom filters work. For more production grade versions of a Bloom filter, we should use implementations found in the larger frameworks with a more robust collection of hash functions. The Bloom filter we see here is presented purely for educational purposes.

Conclusion

To recap our introduction with a few extra details, a Bloom filter is a space-efficient probabilistic data structure designed to quickly test whether an element is a member of a set or collection. It is lightning fast because it only stores a fingerprint of the data being asked for. It does so using a series of hash functions and bit array, but it also does this with a little bit of fuzziness in how accurate its responses are.

That is because Bloom filters are a probabilistic data structure. They are 100% certain when they tell you that an item is not a member of a collection. The fuzziness comes in when they tell us an item is a part of a set. They don't know for sure, so their fast performance and memory efficiency comes at the expense of being spot-on with their answers to the affirmative.

Just a final word before we wrap up. What you've seen here is freshly baked content without added preservatives, artificial intelligence, ads, and algorithm-driven doodads. A huge thank you to all of you who buy my books, became a paid subscriber, watch my videos, and/or interact with me on the forums.

Your support keeps this site going! 😇