Table of Contents
Chances are, growing up, you ran into at least one person who prided him/herself on being able to recite the value of Pi to the bazillionth digit:
3.14159265358979323846264338327950288419716939937510 58209749445923078164062862089986280348253421170679 82148086513282306647093844609550582231725359408128 48111745028410270193852110555964462294895493038196...
Maybe you knew this kid:
Anyway, for most real-world situations, you don't need to go into a whole lot of detail. Something less precise for Pi...such as 3.14159 will do just fine.
This issue of precision will come up quite frequently as you work with numbers in JavaScript. This is where rounding comes in. Rounding a number is all about taking something that is extra precise and making it less precise...for good reason. In this tutorial, you will learn a bunch of tricks on how to do that.
Onwards!
You may be wondering why anybody would want to go from having values that are more precise to having values that are less precise. In this section, we are going to look at some examples.
Whenever you are doing anything on the canvas or positioning DOM elements using code, you'll be doing a whole lot of pixel pushing to the screen. The things you are drawing on screen look best when its position and size values fall on a whole pixel. If you are using fractional values, what you are displaying may end up looking blurry:
An easy way to ensure everything falls on pixel boundaries is to round any position or size value to a whole number.
Working with round numbers is faster than having to deal with numbers that contain extra precision. Nuff said about that :P
JavaScript stores all numbers internally as floating point values. This means your calculations could be subject to floating point shenanigans. Here is an example:
var blah = 0.2 * 0.4;
What do you think the value of blah actually is? If you guessed .08, you would be wrong. Here is what actually shows up:
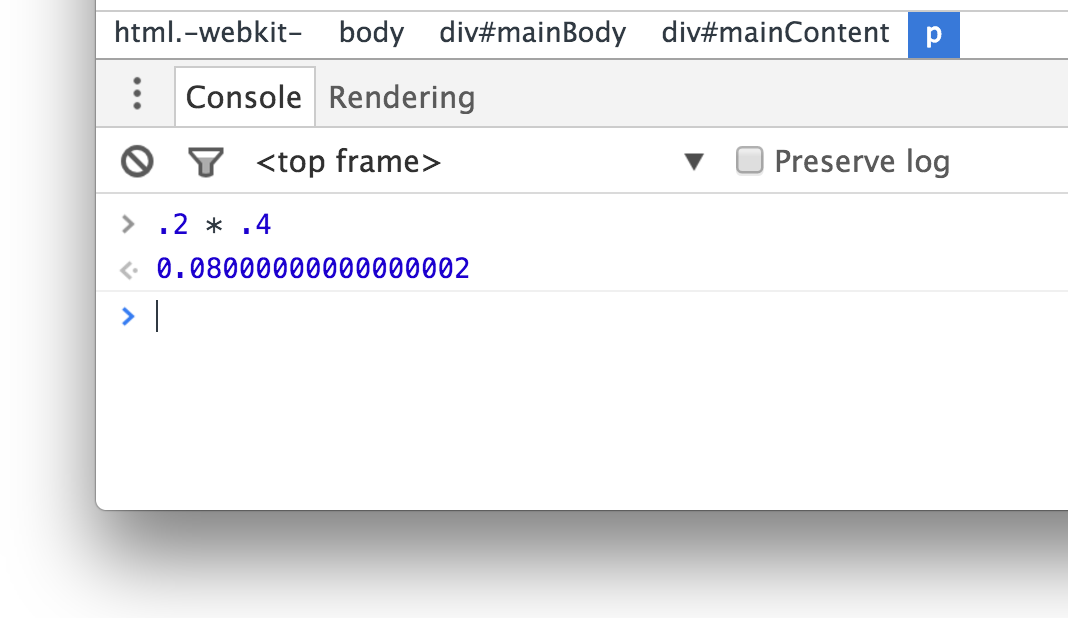
There is a reason why the 2 awkwardly shows up at the end of the result. It has to do with how fractions are represented as floating point values. It is weird, but that's just how it is. By rounding your number, you can account for the unnecessary precision and just get .08 like you probably wanted all along.
Whatever your reason for rounding numbers may be, JavaScript has several ways of allowing you to round numbers. Let us look at the most common ones.
The most common function for rounding your value is the prom king himself, Math.round:
Math.round(1.532); // 2 Math.round(1.235); // 1 Math.round(27.94); // 28 Math.round(0.0005); // 0
This function works by rounding your number to the nearest integer. If the first number after the decimal is 5 or higher, it rounds up. If the first number after the decimal is 4 or lower, it rounds down. The Math.round function most closely resembles what you may have learned in school.
Its equally popular variants are the Math.floor and Math.ceil functions. Whereas Math.round would either round up or down depending on what the number after the decimal is, Math.floor will always round down to the next lowest integer regardless of what the value after the decimal is. Similarly...in an opposite way, Math.ceil will always round up to the next highest integer regardless of what the value after the decimal actually is:
Math.ceil(1.5); // 2 Math.floor(1.5); // 1 Math.floor(1.235); // 1 Math.ceil(0.0005); // 1
All of this should look pretty straightforward. Just to drive the point home about the next highest and lowest integers, let's look what happens when we are dealing with negative values:
Math.ceil(-45) // -45 Math.floor(-45) // -45 Math.ceil(-.5) // 0 Math.floor(-.5) // -1 Math.round(-45) // -45 Math.round(-.5) // -1 Math.round(-1.24) // -1
The Math.ceil and Math.floor functions work as expected. They round up or down to the next largest or smallest integer. Remember, in the negative world, the smaller the absolute value of your number, the larger its actual value:
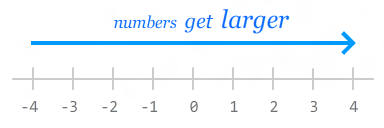
That is why rounding up from -.5 results in you getting 0. If you think of the relative size of numbers as being on the number line, Math.ceil goes right. Math.floor goes left. It's like opposite day over there.
Our prom king Math.round, though, exhibits some slightly shallow behavior. Instead of rounding up or down to the nearest large or small number, this function literally rounds up or rounds down based on the absolute value of the number. That is why rounding -.5 is actually a -1 (a smaller number) than being 0 like you may expect.
In the previous section, you learned how you can round to the nearest integer. There will be times when you want to round to a particular decimal position for extra preciseness. Let's say we want to round our value of Pi to just 2 digits past the decimal point. In other words, we want 3.14159 to be rounded off to 3.14. Using the three amigos (Math.round, Math.floor, and Math.ceil) without any modification will cause our value to either be 3 or 4. That's not what we want.
To get what we want, there is a simple approach we can take made up of just three steps:
To make this more concrete, let's see we want to round 3.14159 to two digits of precision. To get two decimal positions of precision, we can multiply our number by 10 to the power of two (aka 100) and round that value:
Math.round(3.14159 * 100);
Next, divide the result of this rounding operation by 10 to the power of two again to get the answer you are looking for:
Math.round(3.14159 * 100) / 100; // result is 3.14
To generalize this a bit, here is a basic formula:
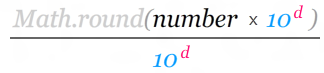
The d stands for the number of places after the decimal point you want to go to. The number is the value you are trying to round. Everything else should be self-explanatory.
Using this model, here is how we can round 3.14159 to the tenths, hundredths, thousandths, and ten thousandths positions:
Math.round(3.14159 * 10) / 10; // 3.1 Math.round(3.14159 * 100) / 100; // 3.14 Math.round(3.14159 * 1000) / 1000; // 3.142 Math.round(3.14159 * 10000) / 10000; // 3.1416
You can substitute Math.round with Math.floor or Math.ceil depending on what exactly you are going for, and the behavior will be predictable.
Normally, I would have something witty to say here. Actually, who am I kidding? My conclusions are usually pretty awful. In fact, nobody even reads this section. I could write whatever I want and nobody would notice. Besides, what is there to conclude about rounding numbers?
Just a final word before we wrap up. If you have a question and/or want to be part of a friendly, collaborative community of over 220k other developers like yourself, post on the forums for a quick response!
