Table of Contents
Master the art of efficient data manipulation and access with arrays, a foundational part of almost every programming language!
We are going to start our deep dive into data structures by looking at arrays. Arrays, as we will find out soon enough, are one of the most popular data structures that many other data structures will use as part of their functioning. In the following sections, we’ll look at what arrays are, why they are so popular, situations they are good in (as well as ones they are bad in!), how to use them, and more.
Onwards!
Let's imagine we are jotting down a list on a piece of paper. Let's call the piece of paper groceries. Now, in this paper, we write a numbered list starting with zero with all the items that we need to pick from the store:

This list of grocery items exists in the real world. If we had to represent this digitally, the data structure that we would use to store all of our grocery items would be an array! Here’s why: an array is a data structure that is designed for storing a collection of data in a sequential order. If we turned our groceries list into an array, what we would have would look as follows:
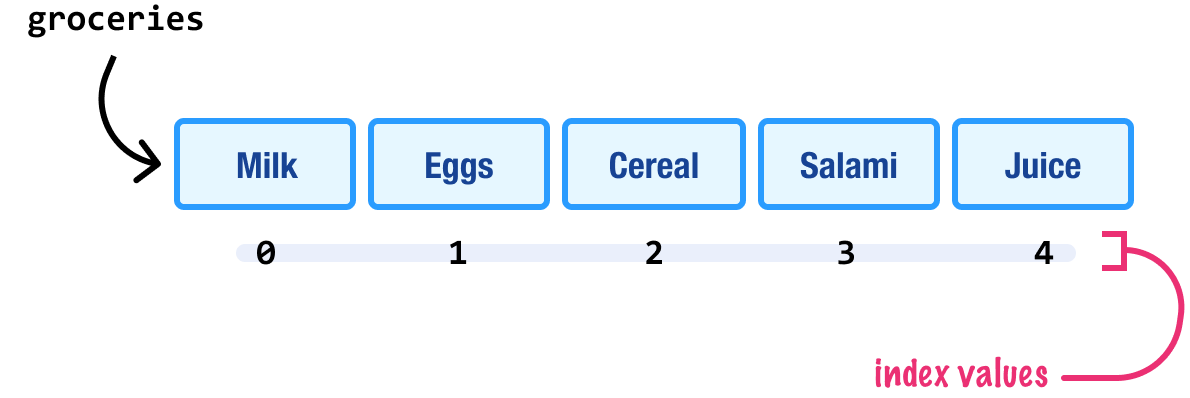
Each item in our grocery list is represented at as an item in our array. These items are adjacent to each other, and they are numbered sequentially, starting with zero. Let’s take our array and put it through some common data operations to help us better understand how it works.
With an array, one of the things we will frequently do is add items to it. Where exactly in the array we add our items is important. The location determines how much work is involved. Adding items to the end of our array is a walk in the park:
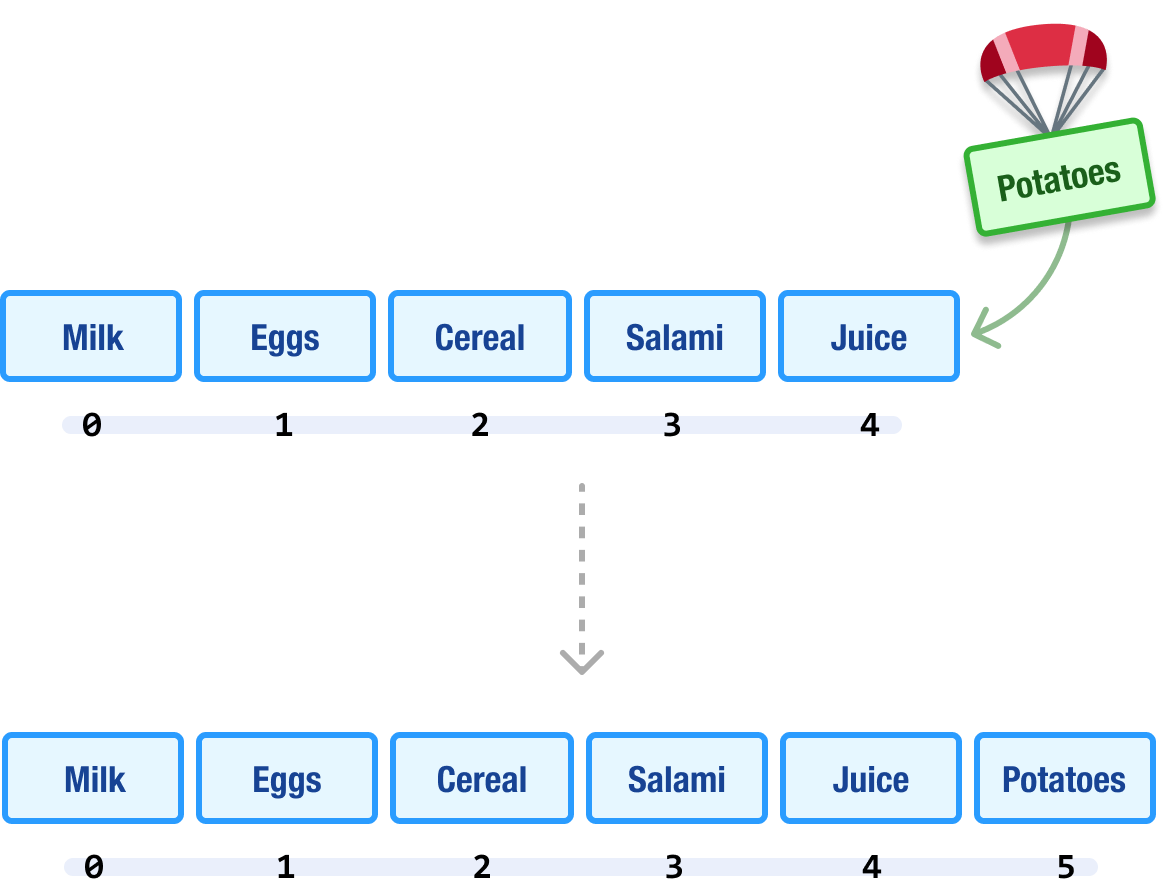
We append a new item to the end. This new item gets the next index value associated with it. Life is simple and good.
When we add an item at the middle or beginning of the array, we first have to make room for the new content:
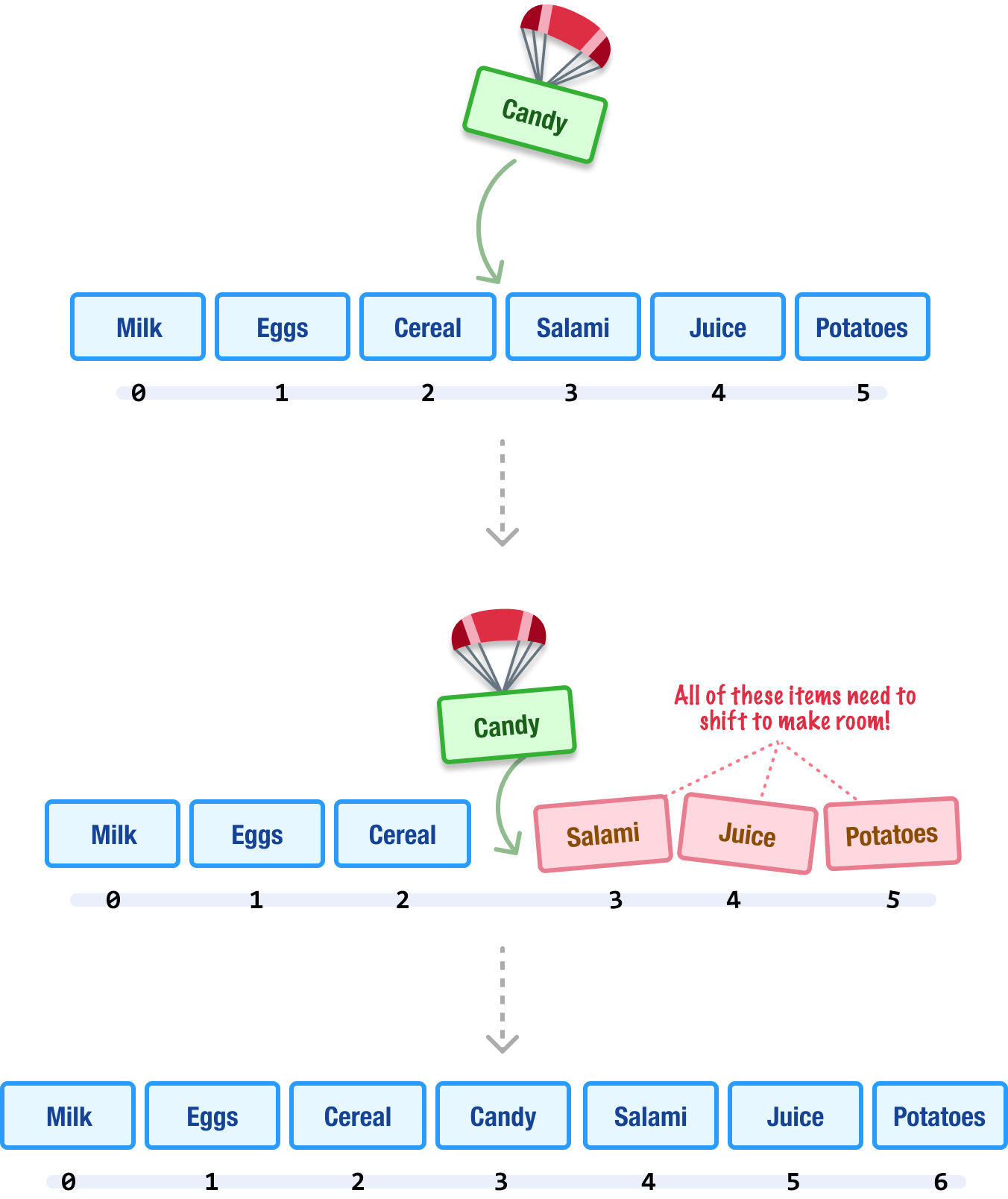
Because arrays are arranged sequentially, making room is a code word for shifting a bunch of array items over and recalculating their index positions. The more items we have to shift, the slower this operation becomes. The worst case is when we insert an item at the beginning, for this means that every item needs to be shifted with their index positions updated. That’s a whole lot of shifting!
When deleting an item from our array, the same challenges we saw with adding items earlier will apply. If we are removing an item at the end, the disturbance is minimal:
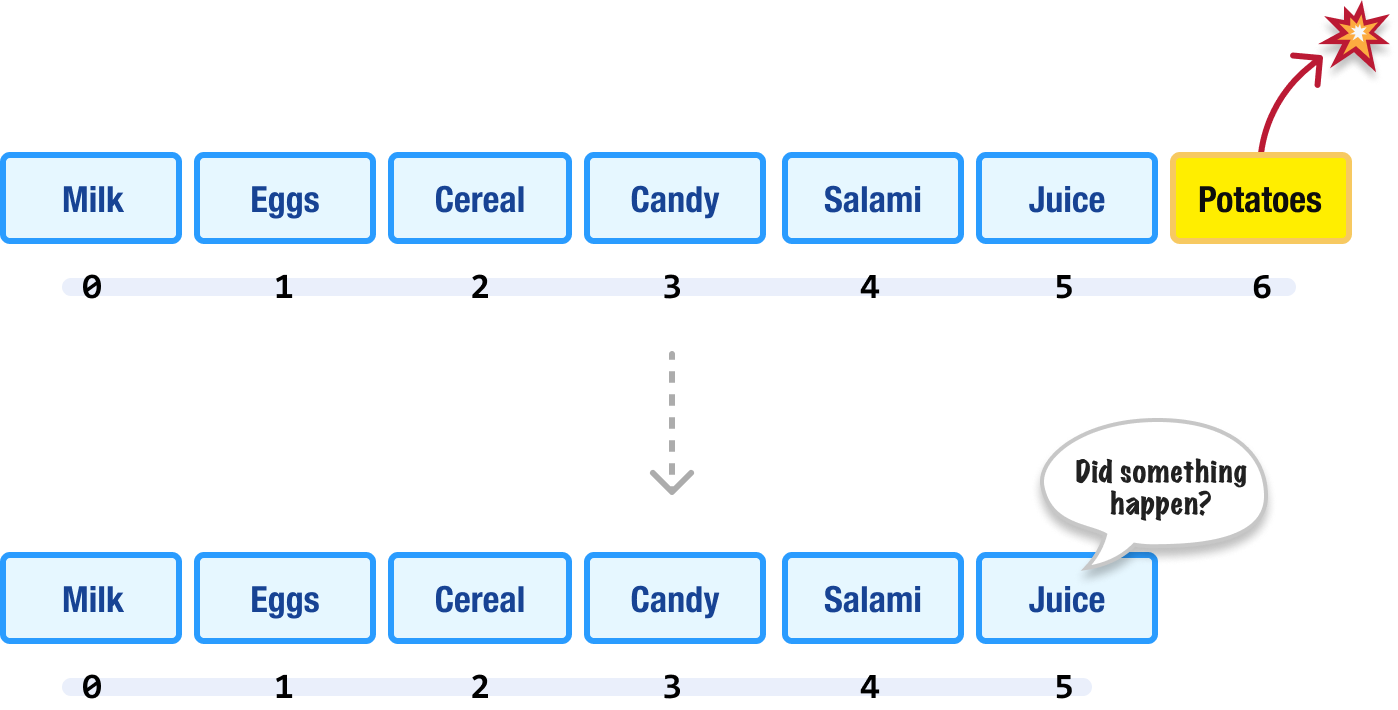
No other array item is affected. If we are removing an item from anywhere else, we need to ensure that all of our array items after the removed item are properly positioned and numbered:
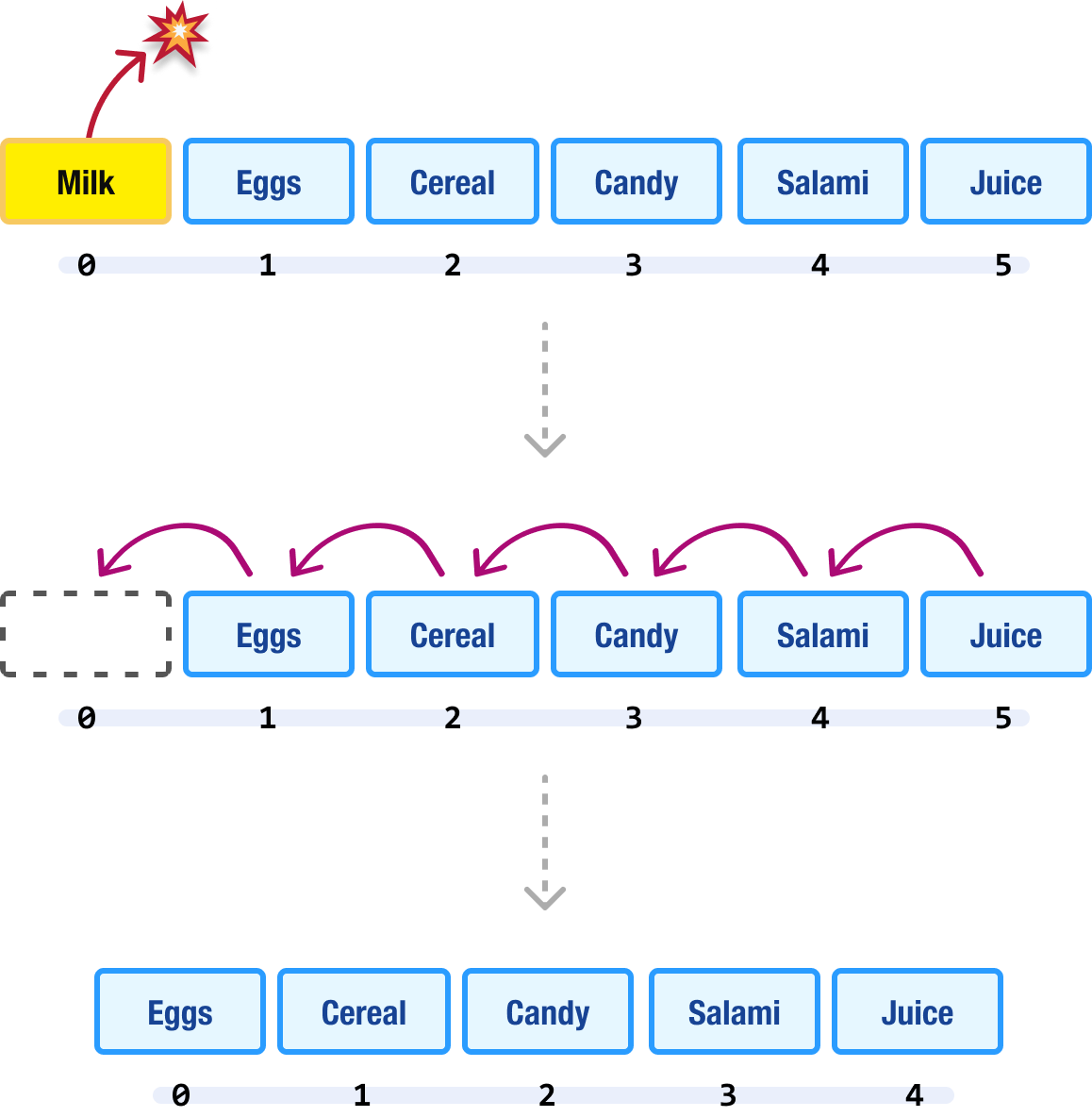
For example, we removed the first item from our array. Every other item in our array now has to shift and recount to account for this change. Phew!
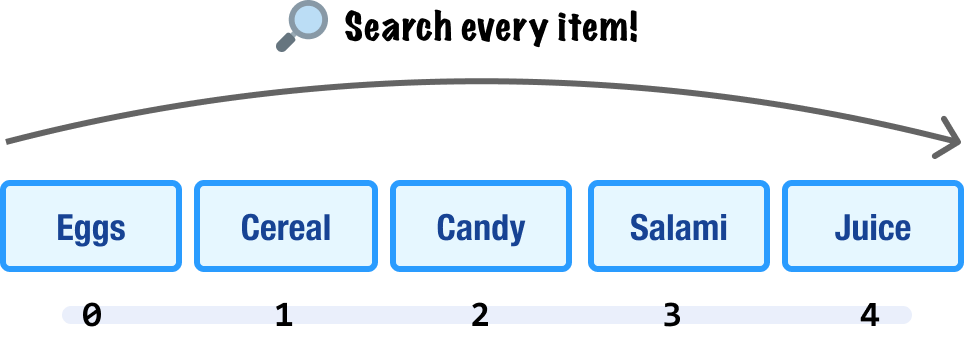
Besides adding and deleting items, we will spend a lot of time searching for items. The most common approach is a linear search where we start at the beginning of our array and go item by item until we find what we are looking for:
Depending on the exact shape of our data, there may be some optimizations we can make. For example, if we know our array’s data is ordered in some way (alphabetically, numerically, etc.), we can employ a binary search to make our search go much faster:
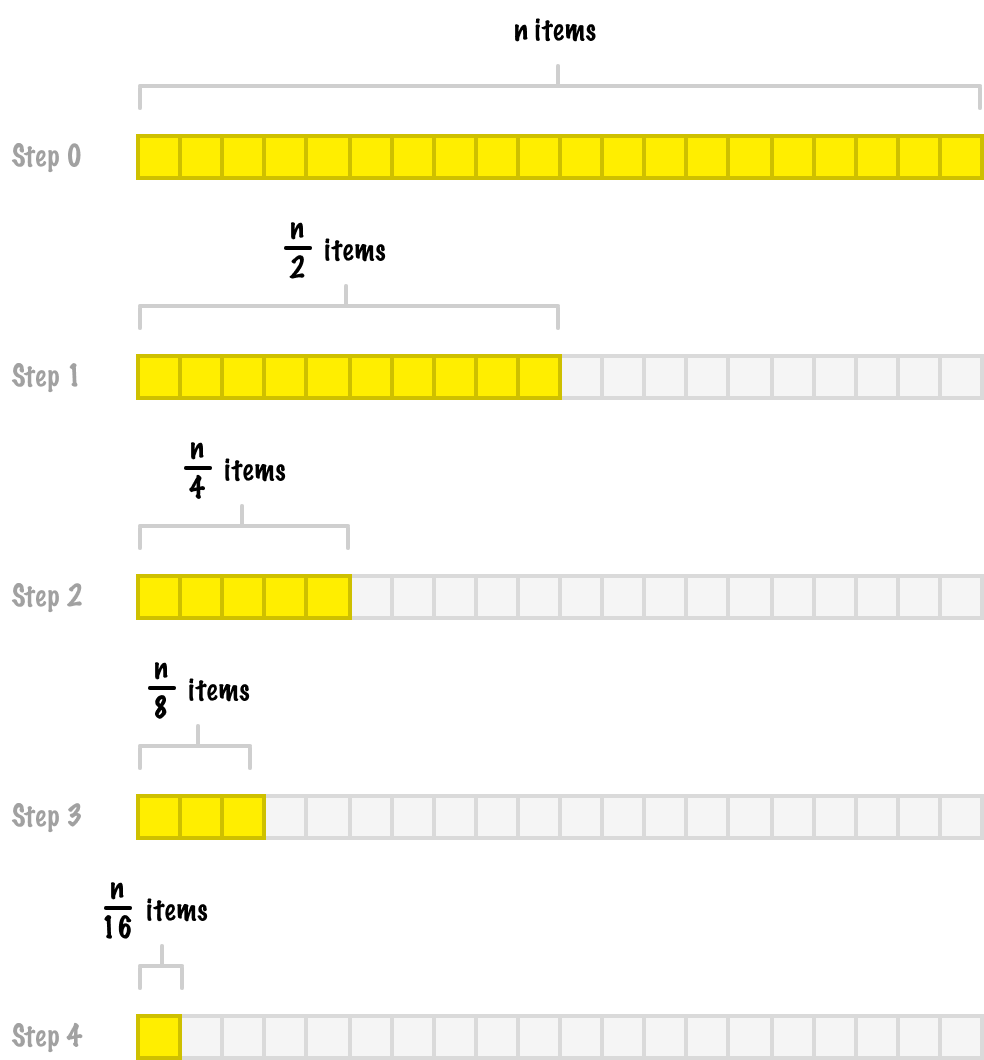
We cover binary searches, linear searches, and other search algorithms a bit later.
We talked about the index position a few times so far, but it is time to go a bit deeper. The index position acts as an identifier. If we want to access a particular array item (via a search or otherwise!), we refer to it by its index position in the form of array[index_position] as shown below:
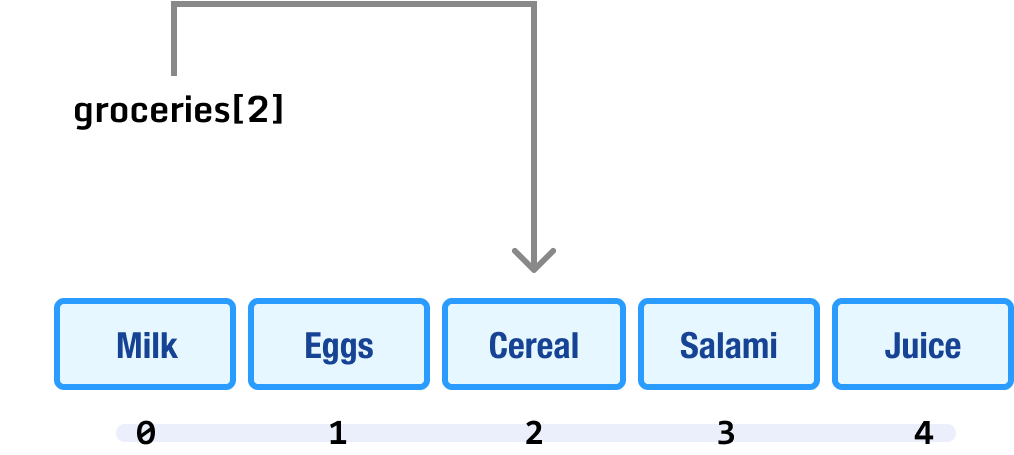
A few tricks to keep in mind are that the first item will always have an index position of 0. The last item will always have an index position that is one less than the total number of items in our array. If we try to provide an invalid index position, we will get an error!
Arrays are a fundamental data structure provided out-of-the-box in almost all programming languages, such as JavaScript! The following are some common examples of how we can use the array to perform some of the operations we called out above:
// Create our array!
let groceries = ["Milk", "Eggs", "Cereal", "Salami", "Juice"];
// Access the first item
let first = groceries[0];
// Access the last item
let last = groceries[groceries.length - 1];
// Access 3rd item
let cereal = groceries[2];
// Insert item at the end
groceries.push("Potatoes");
// Insert item at the beginning
groceries.unshift("Ice Cream");
// Insert item after the 3rd item
groceries.splice(3, 0, "Cheese");
// Remove last item
groceries.pop();
// Remove first item
groceries.shift();
// Delete the 3rd item
groceries.splice(2, 1);
// Find a particular item
let foundIndex = groceries.indexOf("Eggs"); // 1
let itemToFind = -1;
// Iterate through each item
for (let i = 0; i < groceries.length; i++) {
let currentItem = groceries[i];
// Return index of found item
if (currentItem == "Salami") {
itemToFind = i;
}
}For a thorough deep dive into learning the ins and outs of everything arrays do, check out my comprehensive Arrays Guide. If you aren’t familiar with arrays, you should take a few moments and get really familiar with them. Many of our subsequent data structures and algorithms we’ll be learning about will use arrays extensively under the covers.
When working in a modern, high-level programming language like JavaScript, we don’t have to actively think about managing memory. All of the memory handling is taken care of for us. What we are about to look at goes a bit into the inner workings of our computers and the moments where knowing about what goes on will greatly improve our understanding of how things work - things, in our case, being arrays.
When we think of memory, let us simplify them as a series of regions where we can store data into:
Now, our memory is never going to be as clean as what we are seeing here. There will be a bunch of other things our computer is juggling that will be taking up space:
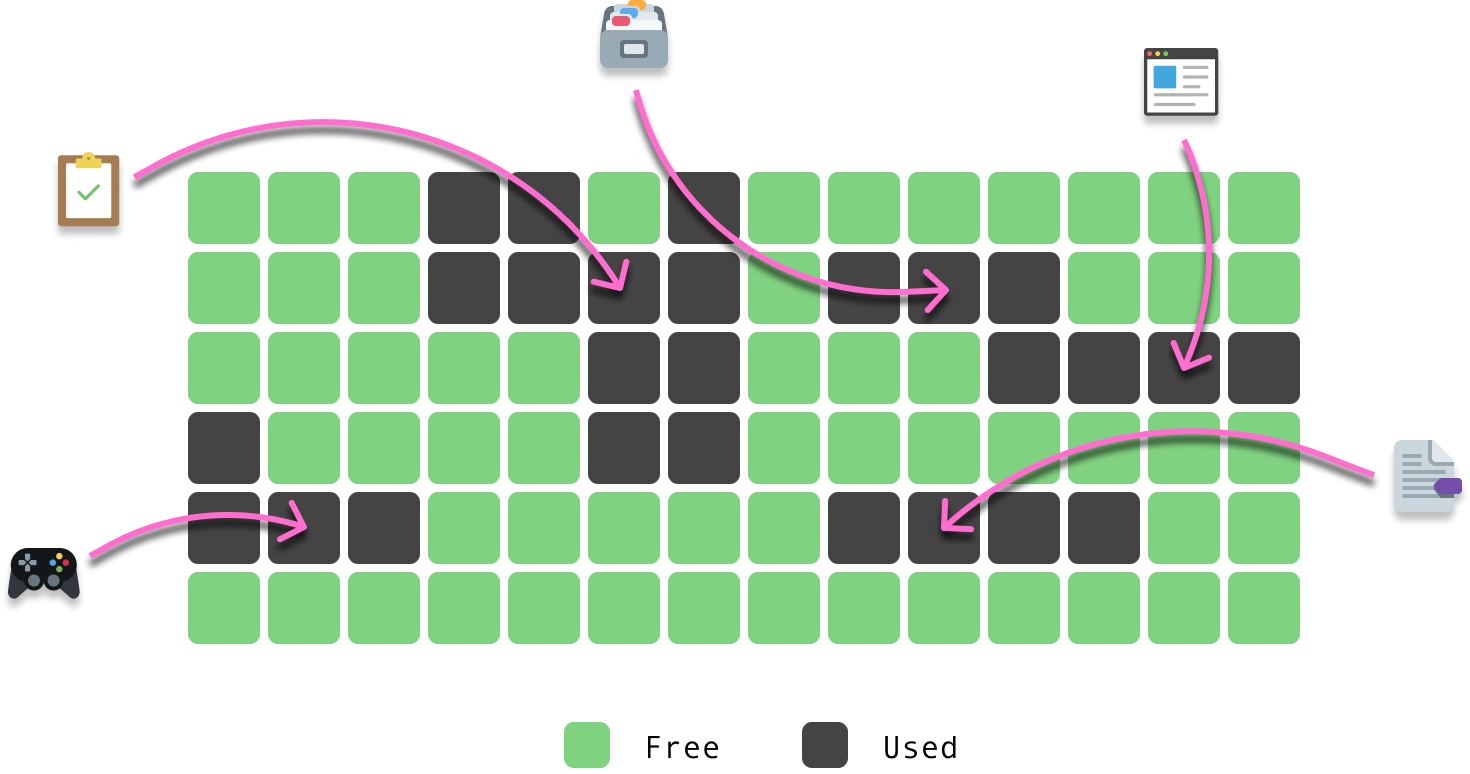
Any new items we add to our memory need to go into the available free regions. This gets us back to arrays. When we create an array, we first need to allocate some space in our memory where it can live. The thing about arrays is that they need to store their items in adjacent (aka contiguous) regions of memory. They can’t be spread across free and used regions.
When we initialize an array, we allocate a fixed amount of space in memory and keep increasing this fixed amount as our array keeps growing. Let’s say we create an empty array. Even though our array is empty right now, we allocate extra regions of memory:
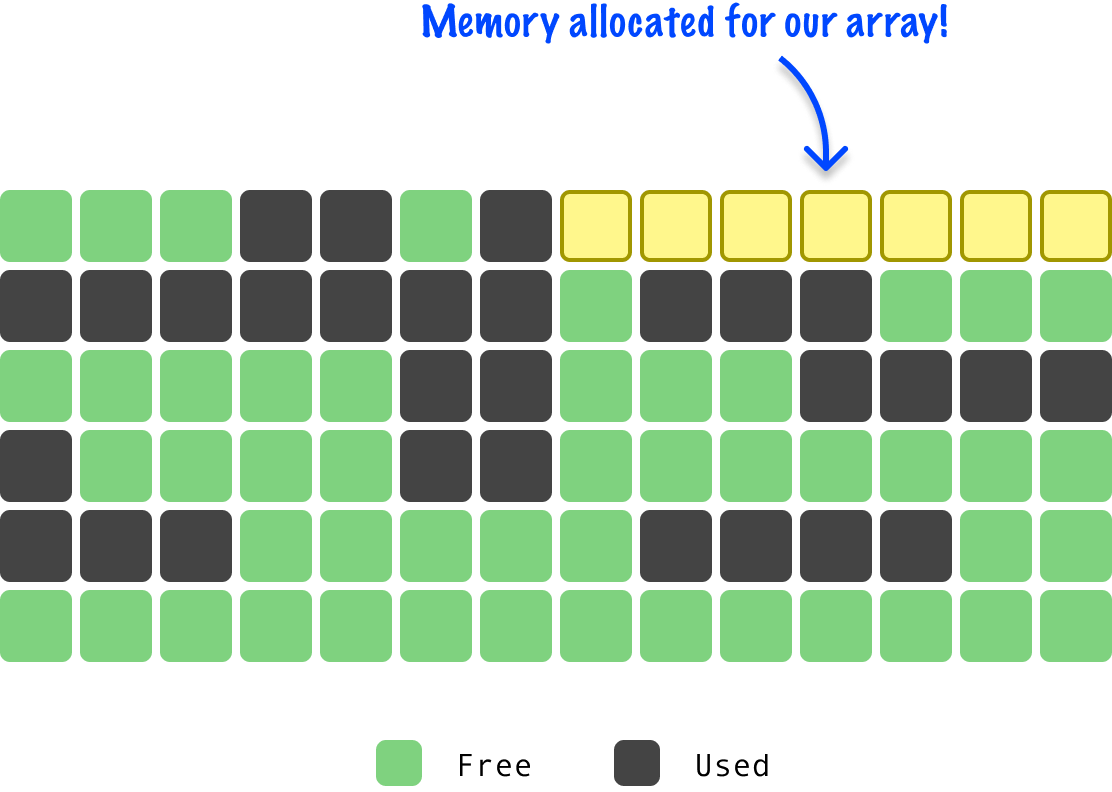
In our example, we have seven regions of memory allocated. As we add items to our array, they will slowly start filling up our allocated memory:
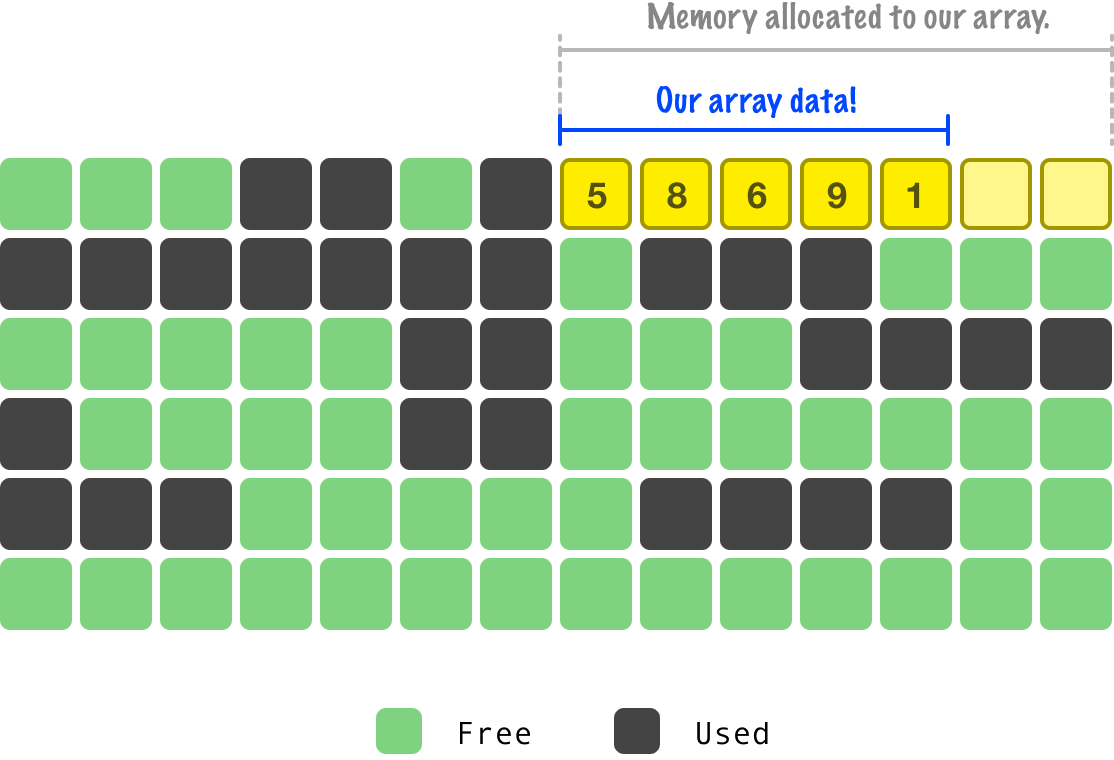
We keep adding data into our array until we fill up all of our allocated space:
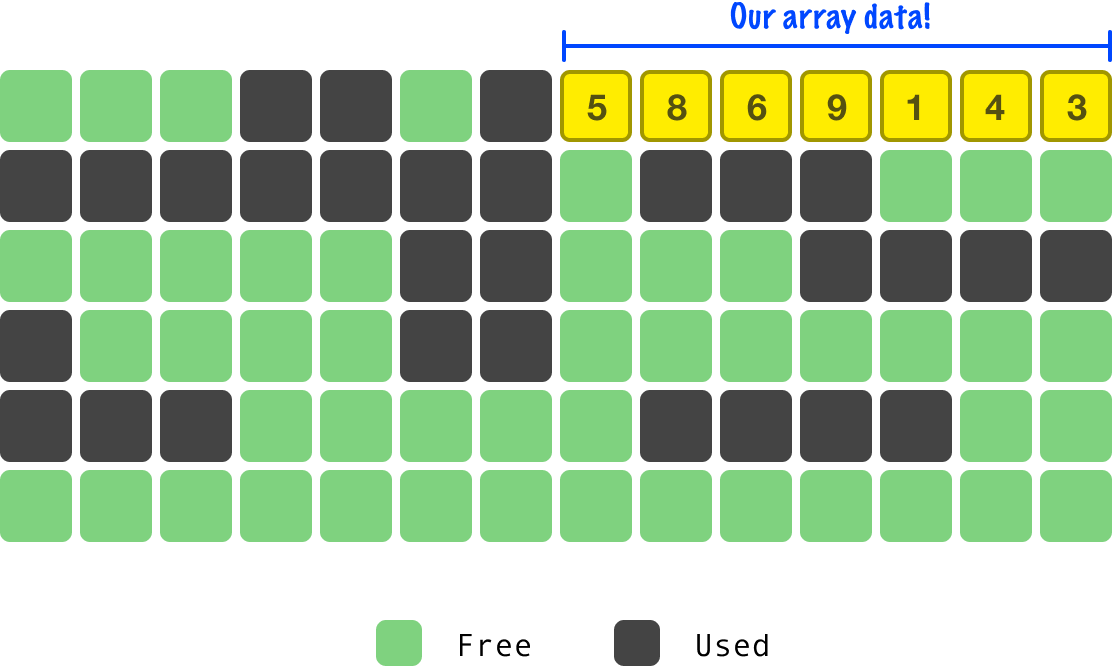
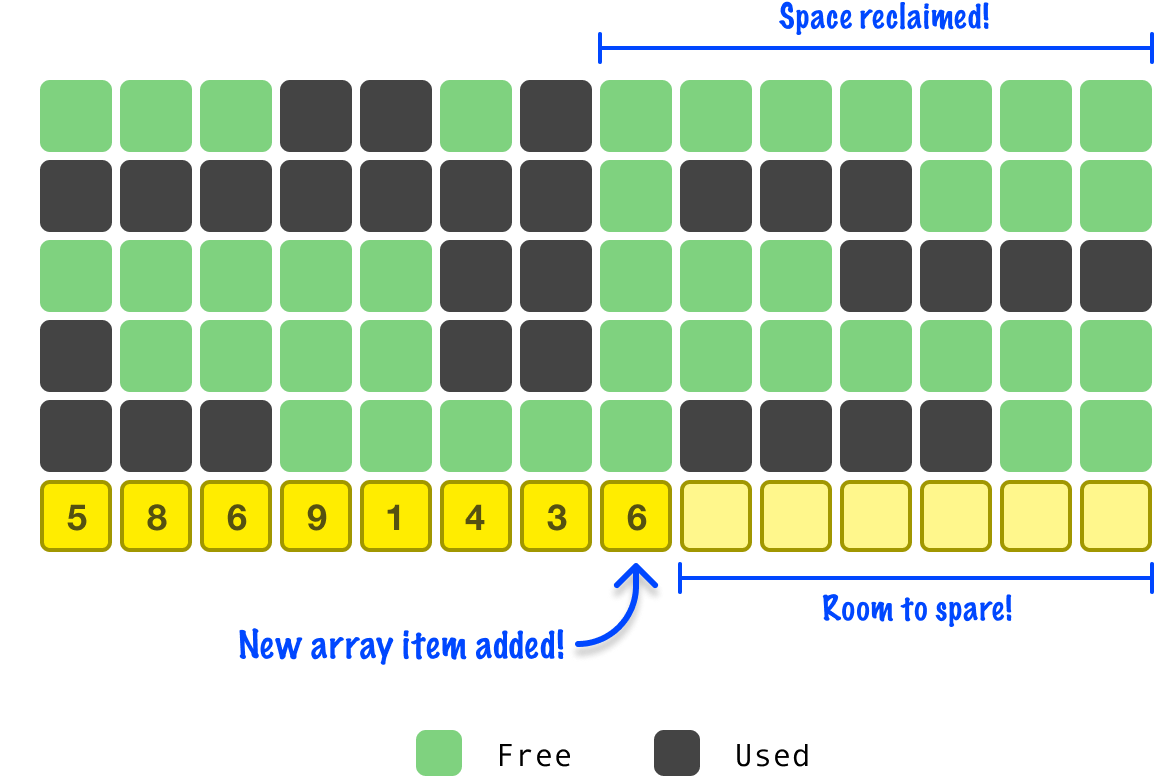
If we add an extra item, what happens next? There is no adjacent memory we can expand our array into. What happens next is that our operating system (or virtual machine) finds an uninterrupted section of memory where our growing array can move into:

Once it finds this region of memory, it is time to move our entire array to this new location:

After our array has fully moved, which is definitely not a cheap operation since every item needs to go to a new position, we can add more array items, and the old memory location our array was in has free space that other things can now go into:
More traditional programming languages were strict about making sure you and I were thinking really hard about memory and how to ensure we don’t go beyond it. Modern languages like JavaScript handle all of this for us, but the performance implications of going beyond our allocated memory size and needing to move our array to a larger region still do apply. We’ll talk about that next.
In the previous sections, we got a glimpse at the sorts of activities that arrays are really fast at (and the activities they are slow at). The following table summarizes the performance and space considerations:
| Action | Average | Worst |
|---|---|---|
| Space / Memory | Θ(n) | O(n) |
| Access by Index | Θ(1) | O(1) |
| Insert at End | Θ(1) | O(n) |
| Insert Elsewhere | Θ(n) | O(n) |
| Delete | Θ(1) | O(n) |
| Delete at End | Θ(1) | Θ(1) |
| Linear Search | O(n) | O(n) |
| Binary Search | O(log n) | O(n) |
Let’s dive into a bit more detail on why our table has the values that it has by looking at each major class of operation!
Array access is highly efficient and has constant time complexity (O(1)). This means that accessing an element at a specific index in an array takes the same amount of time, regardless of the size of the array. Arrays achieve this performance by storing elements in contiguous memory locations, allowing direct access using the index.
There are two classes of search approaches we can take:
We cover both linear and binary searches in greater detail later when covering algorithms, so keep this information under your hat until then.
Arrays are one of the more fundamental data structures we will use. Almost all programming languages, no matter how low-level, will provide built-in support for arrays. There are several reasons for this. In programming, we will be dealing with collections of data all the time. It would be odd to have to re-create the array for every project. The other reason has to do with how arrays work. They closely map continuous regions of memory, and it would be difficult for us (especially higher-level languages) to re-create an array data structure from scratch and maintain the performance that a more native implementation will provide. This is why, as we will see shortly, arrays are actually a part of other data structures that we will be looking at.
Just a final word before we wrap up. If you have a question and/or want to be part of a friendly, collaborative community of over 220k other developers like yourself, post on the forums for a quick response!

:: Copyright KIRUPA 2024 //--