|
Don't worry if the code presented in the
previous page does not fully make sense.
Hopefully after having completed the walkthrough, things
will make more sense. By the end of the tutorial, you will
be able to code all of quicksort in your sleep!
So let's begin the walkthrough. Let's say that you are
interested in sorting the following array of values:

First, we determine the left - i, right - j, and pivot
values. Our left boundary value will be 4, the right
boundary value will be 2, and the pivot value will be the
center value. If you have an even number of items, you pick
the next highest number closest to the center:
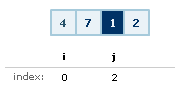
Like before, in all of the images, the dark
blue cells indicate the pivot value.
Right now, we
are still in the light-blue portion of the pseudocode. We've
done nothing but specify the starting positions of our left
and right boundaries as well as determine the pivot value.
Now, let's compare the array values referenced by i
and j with our pivot. Before we do that, we make sure that
the i variable is less than or equal to the j variable. This
ensures that you are not swapping from the wrong sides of
where you are supposed to be. Getting back to the
comparison, we accomplish that using two loops - one loop for the left value, and
another loop for the right value. These loops are indicated
by the white sections of code in the pseudocode image:

Our left loop basically
asks, "Is our left array value less than our pivot?" The answer is
"No", because 4 is not less than 1. That will need to be
fixed, so we end our loop for the left value. In the left
side, we don't move
right to check the next number, for the current number needs
to be swapped.
Let's look at our right loop now. Similar to above, we
ask if our right array value is greater than our pivot?
Unlike last time, the answer is "Yes", for
2 is greater than 1. So we continue our loop and decrement
our j variable by 1 to analyze the next value:

We are still within the right-sided j
loop, so we continue our questioning of the current value. Is
the value at j greater than our pivot? No, for both the
pivot and the number referenced by j are the same value - 1.
So we end the loop for j much like we did
for i.
Onwards to the next page!
|