|
In the previous page,
I provided you with the Flash code needed to use and test
quicksort. But, the code itself is not that interesting
unless you actually understand how quicksort works. Let's
start with our introduction of how quicksort works!
Like mentioned earlier, quicksort works by dividing the
input into several smaller pieces. The key to its speed is
knowing when to divide the input into smaller pieces and
when to just perform operations on the data. I will first
provide a simple overview of how quicksort works, then I
will provide a more detailed look at how the major parts of
the overview work by demonstrating a small example, and I
will then conclude with a line-by-line analysis of how our
code turns our understanding of quicksort into
machine-understandable actions.
Let's imagine that the following grid of squares represents
our array of numbers. Imagine that each square contains a
random number in it:

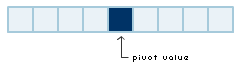
Quicksort works by initially picking an item in your list
of items called a pivot. Let's pick our pivot number
to be somewhere in the middle of the list, but your pivot
value can be anywhere. For the above array, the pivot is
colored in dark blue below:
Your pivot value is actually quite important. Quicksort
will use the pivot value to order items. For example, in
quicksort, all items to the
left of the pivot value should be smaller, and all items to
the right of the pivot value should be
larger. In other words, you are basically dividing your
original input into two pieces - one piece that contains all
values that are smaller than the pivot, and another piece
that contains all values that are larger than the pivot.
With that constraint in mind, this is how our list would
look like:
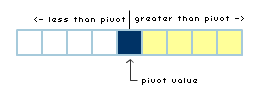
In the above example, the area shaded in white contains
values less than the pivot value, and the area shaded in
yellow contains values greater than the pivot value. The
goal of this operation is to simply divide the values up.
You can guarantee after completion of the above step that no
value to the right of the pivot is larger than any value on
the left side of the pivot, and you can also guarantee that
no value to the right of the pivot is smaller than any value
in the left of the pivot.
You now have two sections of data - less than
pivot and greater than pivot. What you
basically do now is repeat the above divide process for each of
those two sub-divisions of your input. Quicksort works by
recursively calling itself on each subsection of data:
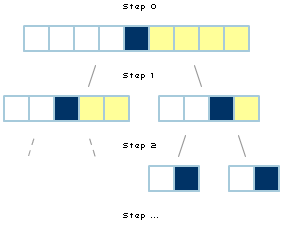
Each division creates two sets of data from your earlier
list, and each of them have a new pivot value. Each of the
sets of data will loosely organize themselves around the
pivot point, divide again, arrange themselves, divide...you
get the picture. You will basically create a recursion of
divisions until the final sub-section is perfectly sorted,
which it will in the end by this method.
More explanations on the next
page!
|