Trigonometric Animations - Page 1
       by kirupa  |  2 October 2009

In the previous page, you learned a bit about trigonometric animations at a very high level. In this page, let's go a little deeper and look at how these functions can be represented in code.

Cosine and Sine in Code
There are three common trigonometric functions - Cosine, Sine, and Tangent. For animations, you will rarely use Tangent, so let's just focus on Cosine and Sine. In ActionScript, the syntax for accessing them both is:

Math.sin(number);

Math.cos(number);

If you take a graphing calculator, if you graph the above two functions, you would basically get the exact chart you saw in the previous page. The value you pass in as an argument to Math.sin() or Math.cos() is the angle, and that is what you see on the x-axis.

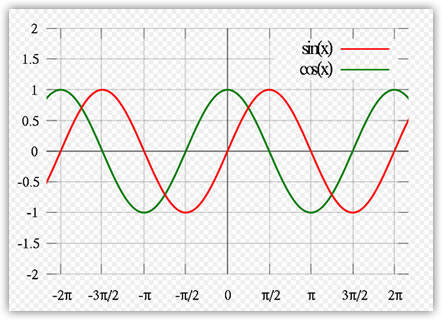
Compare the values from the chart to what I input into Flash below:

// 0

Math.sin(-2 * Math.PI);

 

// 1

Math.sin(-1.5 * Math.PI);

 

// 0

Math.sin(-1 * Math.PI);

 

// -1

Math.sin(-.5 * Math.PI);

 

// 0

Math.sin(0 * Math.PI);

 

// 1

Math.sin(.5 * Math.PI);

 

// 0

Math.sin(1 * Math.PI);

 

// -1

Math.sin(1.5 * Math.PI);

 

// 0

Math.sin(2 * Math.PI);

I basically took the key angles from our chart and placed them into Flash just to show you how to map between the chart and code. If you pass in any other intermediate angle, you will find that your output is exactly the same as what it would be if you relied on the chart, but the chart makes it a bit difficult to read values that are not -1, 0, or 1.

Note
Notice I am entering the angle by using the built-in constant for PI (Math.PI) instead of just approximating to 3.14. I am doing this to ensure the result is exactly the same as that of the chart, but you do not have to do this.

You can definitely use decimals as well, for PI is nothing more than 3.14159.... The only thing to note is that, by going all decimals, you do lose a certain amount of precision. Keep that in mind if such precision is important to you! For example, Math.sin(PI) is 0. Math.sin(3.14159) is 0.000002653589793352726. The answer is close to 0, but close may not be quite right.

Creating a Simple Animation
Now that you have seen the code for usng the Sine and Cosine functions, let's look at placing them in a simple application. I have created a simple application for you to get started on, so please download it from the following location:

  Download Partial Source Files

Don't worry. The application I have provided just saves you some time without giving away anything that might be important. All I have done is created a ColorfulCircle movie clip class, drew instances of that class on the artboard, and added an ENTER_FRAME event handler. In case you are curious, you can learn in detail how this was all done in the Classes and MovieClips tutorial.

Anyway, once you have downloaded and extracted the files, go ahead and open both trig_animation_flash.fla as well as ColorfulCircle.as. The Flash file only contains a few circles:

[ what your artboard looks like ]

These circles are instances of the the ColorfulCircle movie clip, and this movie clip has an associated class file that is stored in the ColorfulCircle ActionScript file. If you switch over to that file, you will find the following code:

package {

import flash.display.*;

import flash.events.*;

import flash.geom.*;

 

public class ColorfulCircle extends MovieClip {

 

public function ColorfulCircle() {

this.addEventListener(Event.ENTER_FRAME, flyCircleIn);

}

 

function flyCircleIn(e:Event) {

 

}

}

}

If you run your application right now, nothing will happen. The reason is that we haven't actually specified what our application will do. That's what the next page is for!

Onwards to the next page.

1 | 2 | 3 | 4