|
by
kirupa | 2 October 2009
This title may sound scary to you, and it probably isn't
because of the word Animations. The word
trigonometric to many of you brings up memories of school with
random repeating graphics, cosine, sine, and Pi. Don't worry if you forgot everything about
trigonometry or never had a chance to learn it. That is OK
for today, for my goal with
this article is to emphasize just the portions of
trigonometry that make sense when used in animations.
For example, the following animation may just look like a bunch of
circles just flying around after you mouse over the button:
Looking deeper, there is a bit more to it. This effect, dubbed the
Colorful Explosion by me, uses some trigonometric magic.
De-mystifying this magic is where this tutorial comes in. By the end of this
article, you will have gained the ability to learn how the
above and a range of other animations can be created using
just trigonometric functions.
There is really only one thing that characterizes
trigonometric motion. That one thing is
periodicity or, to put
more simply, predictability. All trigonometric animations
fall into a predictable pattern - almost too predictable
actually.
For example, two common trigonometric functions you will
be using are Cosine and Sine. These functions take a number as
the input and return another number as the output.
Regardless of how large or small the input is, the number
that gets returned is always, by default, between -1 and 1:
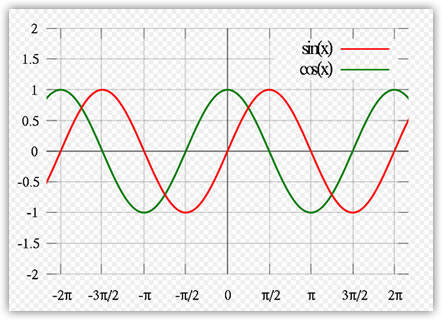
[ image plotting Cosine and Sine taken
from
wikipedia ]
Let's look at the above chart in greater detail. The
input to the function is an angle similar to what you see on
the x-axis. The angle is in terms of radians, so that is why
you see the Pi symbols. When the Cosine and Sine functions
that the angle as the input, they return a value known as
the amplitude. This amplitude is what is
plotted on the y axis.
One characteristic of trigonometric animations I
mentioned is periodicity. In the above graph, let's focus in
on the Sine function. Notice that the range of angles shown
in the graph goes from -2 Pi (-6.28) and 2 Pi (6.28).
Despite the range of the angles, notice that the amplitude
never deviates beyond -1 or 1. Even an angle of 1000 Pi
would result in a value between -1 and 1.
The periodicity also means that you do not need to look
over every possible angle to figure out what the value of
your Cosine or Sine function will be. What you need to find
is a single tile of your Cosine or Sine function that you
can repeat forever without ever having lost any fidelity in
your pattern.
For example, this is would be considered an example of
such a tile:

This would be another example of a tile:

For a simple cosine function, the tile's range of angles
will be 2 PI. Something from negative PI to positive PI or
something from 0 to 2 PI would all work because the range of
angles between those endpoints contains 2 PI worth of them!
Ok, this page was a little dry. I will make up for this
on the the
next
page where we jump right into some code.
Onwards to the
next page.
|