Depth First and Breadth First Search - Page 3

In the previous page, you learned how to use Depth First Search to find a solution to a search problem. In this page, I will explain how Breadth First Search will find a solution to a similar search problem.

Breadth First Search
The reason I cover both depth and breadth first search methods in the same tutorial is because they are both similar. In depth first search, newly explored nodes were added to the beginning of your Open list. In breadth first search, newly explored nodes are added to the end of your Open list.

Let's see how that change will affect our results. For reference, here is our original search tree:

Let's try to find a path between nodes A and E.

Step 0
Let's start with our root/goal node:

Like before, I will continue to employ the Open and Closed Lists to keep track of what needs to be done:

• Open List: A

• Closed List: <empty>

Step 1
Now, let's explore the neighbors of our A node. So far, we are following in depth first's foot steps:

We remove A from our Open list and add A to our Closed List. A's neighbors, the B and C nodes, are added to our Open list. They are added to the end of our Open list, but since our Open list was empty (after removing A), it's hard to show that in this step.

Our current Open and Closed Lists contain the following data:

• Open List: B, C

• Closed List: A

Step 2
Here is where things start to diverge from our depth first search method. We take a look the B node because it appears first in our Open List. Because B isn't our intended destination, we explore its neighbors:

B is now moved to our Closed List, but the neighbors of B, nodes D and E are added to the end of our Open list:

• Open List: C, D, E

• Closed List: A, B

Step 3
We now expand our C node:

Since C has no neighbors, all we do is remove C from our Open List, add it to the end of our Closed List, and move on:

• Open List: D, E

• Closed List: A, B, C

Step 4
Similar to Step 3, we expand node D. Since it isn't our destination, and it too does not have any neighbors, we simply remove D from our to Open list, add D to our Closed List, and continue on:

• Open List: E

• Closed List: A, B, C, D

Step 5
Because our Open list only has one item, we have no choice but to take a look at node E. Since node E is our destination, we can stop here:

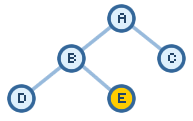
Our final versions of the Open and Closed Lists contain the following data:

• Open List: <empty>

• Closed List: A, B, C, D, E

Traveling from A to E takes you through B, C, and D using breadth first search. In the next page, I will summarize the algorithm for both our search methods and cover the Flash code needed to re-create them.

Onwards to the next page!

1 | 2 | 3 | 4 | 5 | 6 | 7