If there ever was an award for a topic that sounded extremely boring but was also extremely useful, then this whole finding the middle element in an array would probably take the cake. We directly or indirectly rely on finding the middle element in a variety of situations.

In statistics, the middle element in an array is crucial to helping us calculating the median value. In data visualization, if we are trying to distribute a collection of data across two columns as equally as possible, we’ll want to know where the middle element is to figure out how many elements will be shifted between each column:

In the happening world of algorithms, finding the middle element is core to how algorithms like binary search, quicksort, mergesort, and many others work. The short of it is this: knowing how to properly find the middle element in an array is an important skill for us to get awesome at. This tutorial is going to help.

Onwards!

General Approach

To find the middle element in an array, there are a few things we need to take into account. If we look at this problem generally and not in terms of code or anything technical, the general way we find the middle of something is by first measuring the distance from end-to-end...as highlighted by this totally stylish and hip t-shirt:

We then divide the distance we measured by two. The number we get after this division is the middle point. If we mark or cut our t-shirt along this middle point, we will have divided our t-shirt into two halves:

This seems fairly straightforward, right? If we turn what we know so far about finding a t-shirt’s middle point into the happening world of arrays, we can take a similar approach after taking into account one gigantic difference. A t-shirt’s middle point can be defined along any arbitrary line. Arrays don’t work that way. They are made up of a finite number of individual items. When dealing with finite items, finding the midpoint requires some special consideration.

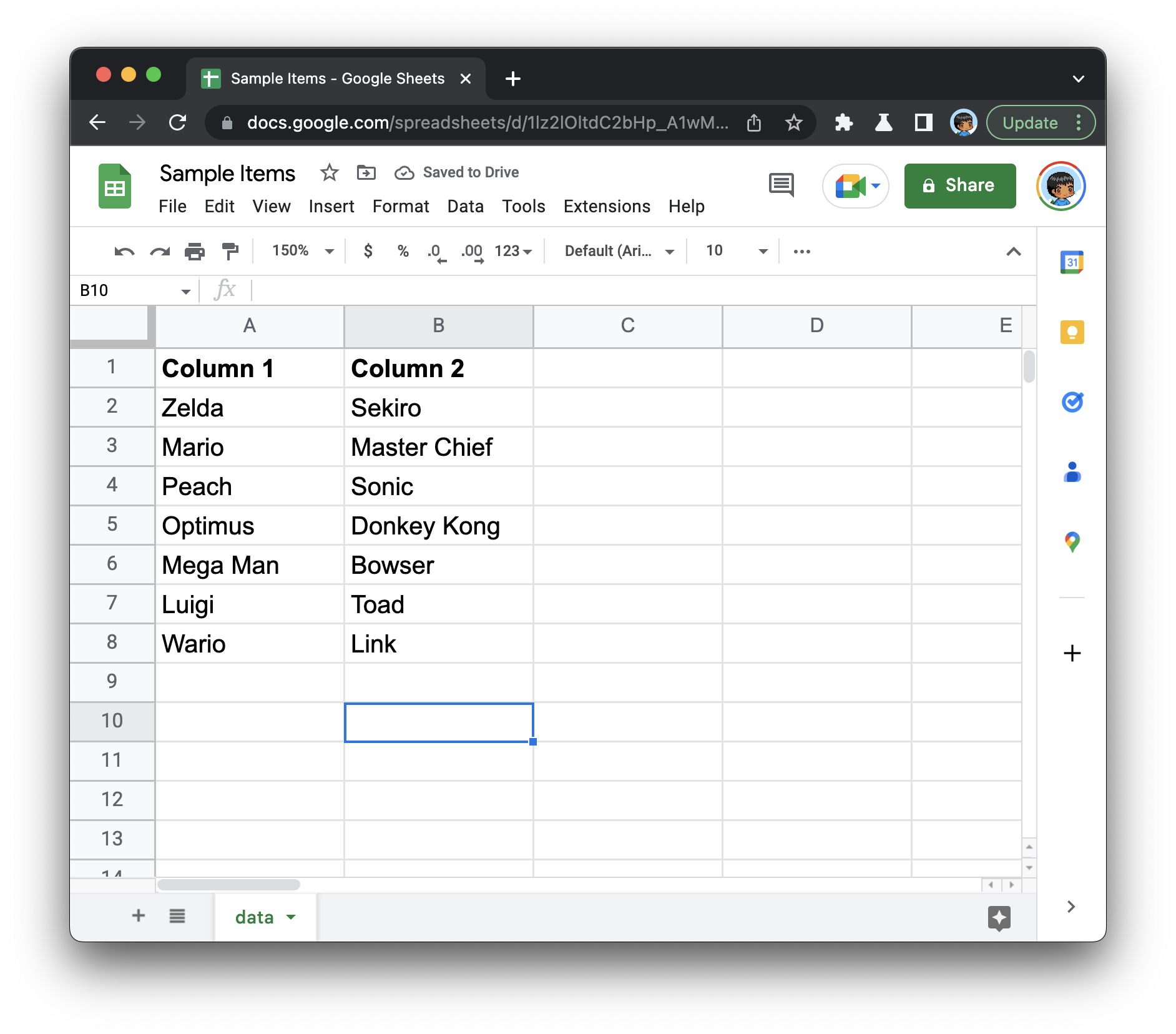
If we are dealing with an odd number of items, this is easy:

The middle point is a clean array index position. The starting index is 0, the ending index is 8, and the middle point is going to be index position 4.

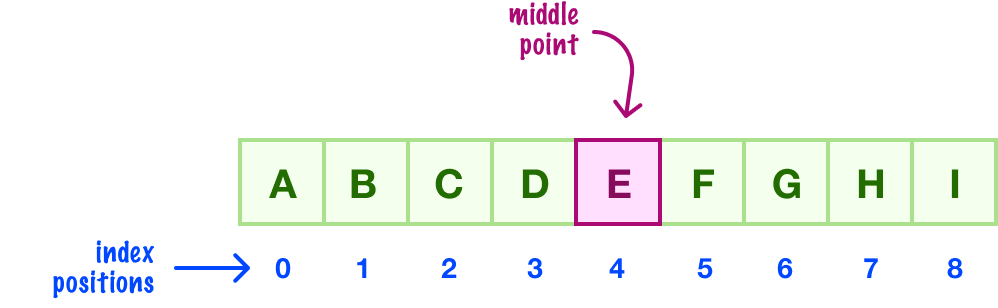
With an even number of items, finding the middle point requires an extra step. Below we have an array with eight items:

If we tried to find the middle between our starting index of 0 and ending index of 7, we’ll end up with a value of 3.5:

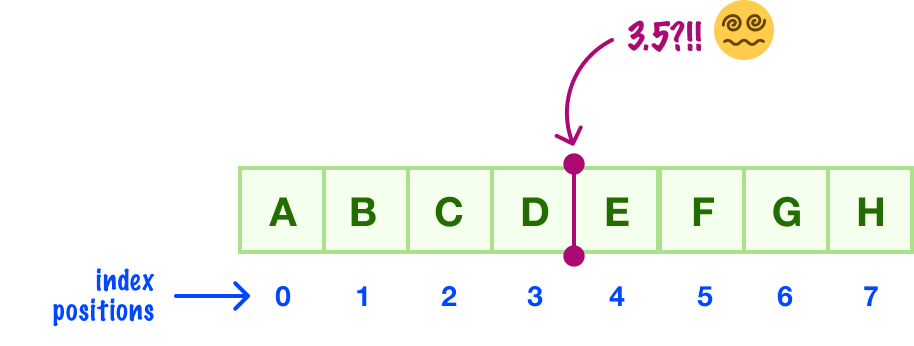
There is no index position of 3.5, for the index position needs to always land on an integer! What we would do in these cases is round our value down to the closest integer. Our 3.5 becomes 3:

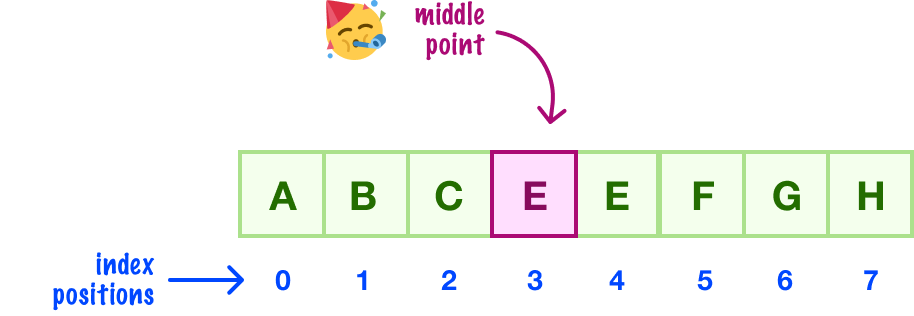
Suppose we had to generalize our logic for finding the middle element that works for arrays containing both even and odd numbers of items. In that case, we can use the following formula:

The value for start is the starting index position, and the value for end is our ending index position. By using Math.floor, we ensure the value we get for the middle position is always a whole number.

JavaScript Time

If we took all of the words and diagrams we saw in the previous section, we can find the middle index position for an array with just this one-line expression:

let middleIndex = Math.floor((start + end) / 2);

Putting this all together, here is how this expression can be used to find an array’s middle element:

let oddArray = ["A", "B", "C", "D", "E", "F", "G", "H", "I"];

let middleIndex = Math.floor((0 + oddArray.length -1) / 2);
console.log(oddArray[middleIndex]); // E

If we are finding the middle element for an entire array, the value for start will always be 0. The value for end will be the length of the array minus 1 (array.length - 1) as shown in this code snippet.

In many situations, especially those involving our friendly search and sort algorithms, we’ll want to find the middle element in a subsection of our array. During those times, the values for start and end will be a region within a larger array as opposed to the start and end of one.

Just a final word before we wrap up. If you have a question and/or want to be part of a friendly, collaborative community of over 220k other developers like yourself, post on the forums for a quick response!