Master negabinary (base (–2)) with visual examples! Learn how to count, convert, and do math without sign bits in this fun guide to negative-base numbers.

In our earlier look at non-decimal number systems that our computers love, we learned how to work with binary (base-2) and hexadecimal (base-16) values:

Today, we are going to go one step further. We are going to take everything we learned and look at how to work with negabinary or base-(-2) numbers. That is right! We are going to learn all about base negative two.

Onwards!

Why Learn Negabinary (base-(-2))?

Unlike binary and hexadecimal values, which can be found all over the place with just a little bit of digging in the right spots, negabinary values are more rare. Unless you are doing something very specialized, you’ll likely never run into it. The way I ran into it was purely by accident. I was reading this interview with the legendary computer programmer Charles Simonyi.

In this interview, he mentioned that one of his favorite interview questions was the following involving negabinary values:

With all of this said, learning about negabinary numbers isn’t just for trivial purposes. There are some interesting quirks when dealing with negative base values that may come in handy in unexpected ways. In the following sections, let’s dig deeper into how negabinary numbers work and wrap things up by also answering Charles’s question.

Understanding Negabinary Numbers

Negabinary works similarly to binary in that the output numbers we’ll be dealing with are just 0’s and 1’s. There is a crucial twist, though. Each position in the negabinary base-(-2) system represents a power of -2 rather than 2. This means the place values alternate between positive and negative powers of 2.

Going from Decimal to Negabinary

To convert a number from decimal to negabinary), we’ll use the general approach we’ve seen a few times already when looking at binary and hexadecimal values. We repeatedly divide the decimal number by the base value (-2 in our case) and record the remainder that is in the range of the expected output (either 0 or 1). We keep repeating this until the quotient from all our dividing reaches 0. Once that happens, we group all of the remainders together from the bottom to the top. This grouping of remainders is our converted output.

With negabinary, there is a twist that revolves around our specific handling of negative remainders. This last detail is important, and we’ll cover that when we run into it. To help bring all of this to life, let’s start with an example. What we want to do is represent the number 42 in negabinary.

First, we start off by dividing 42 / -2, and this results in a value of -21 with a remainder of 0:

42 / -2 = -21 remainder 0  

This all seems straightforward. The next calculation will be to divide -21 by -2. The result will be 10 with a remainder of -1:

42 / -2 = -21 remainder 0  
-21 / -2 = 10 remainder -1 // Wait...is this allowed?

Now, here is a problem. Valid negabinary values can only be 0 or 1. A remainder value of -1 isn’t valid, so what do we do? We adjust the quotient and the remainder while keeping the relationship between the values valid:

More specifically, we adjust by adding:

• 1 to the quotient
• 2 to the remainder

With these changes, our quotient is now an 11, and our remainder is increased by 2 to now become a positive 1.

Taking a step back, what we did isn’t arbitrary. We “borrowed” 1 from the quotient and “paid back” with 2 in the remainder. We essentially rewrote the same number in a way that conforms to the negabinary's digit rules. We didn't change the math — we just expressed it in a format that fits base –2.

To validate that there was no funny business, this algebraic formula explains the relationship between the divisor, dividend, quotient, and remainder:

If a / b = c remainder d, then bc + d = a

Using this approach, when we plug in the appropriate post-adjusted values...

-21 / -2 = 11 remainder 1, then -2 * 11 + 1 = -21

...we can see how everything squares up nicely with a result of -21.

Continuing this approach as we keep dividing the quotient by -2 and course correcting to ensure we only get valid 0 or 1 remainders, the full series of steps until our quotient hits 0 is:

42 / -2 = -21 remainder 0  
-21 / -2 = 11 remainder 1  
11 / -2 = -5 remainder 1  
-5 / -2 = 3 remainder 1  
3 / -2 = -1 remainder 1  
-1 / -2 = 1 remainder 1  
1 / -2 = 0 remainder 1

Collecting all of the remainders up from the bottom, we get 1111110. This 1111110 value is the negabinary representation of 42.

Going from Negabinary to Decimal

It’s time for us to go the other way around and look at the steps it takes to go from a negabinary value to a decimal value. This approach is FAR less dramatic. The main work is for us to map our negabinary values to their equivalent powers of -2:

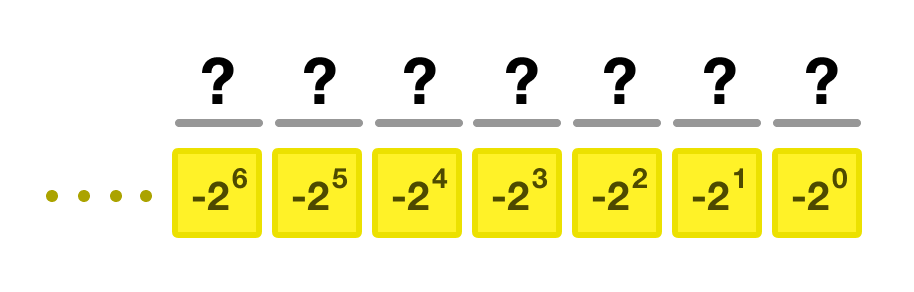
If we do this mapping for the negabinary value of 1111110, we will start at the right-most value and start incrementing the power of -2 as we go left and have no more values to map at the end. Starting from 0, we increment the power by 1. For this example, our mapping will look as follows:

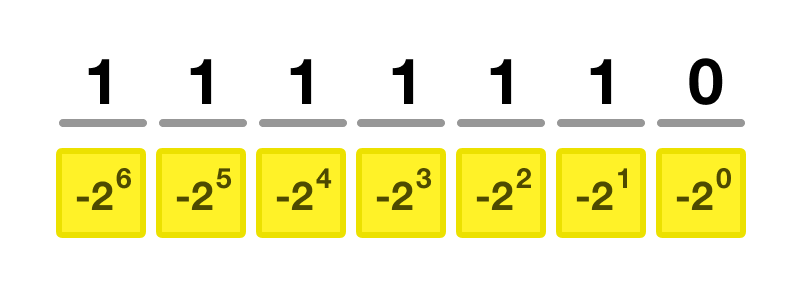
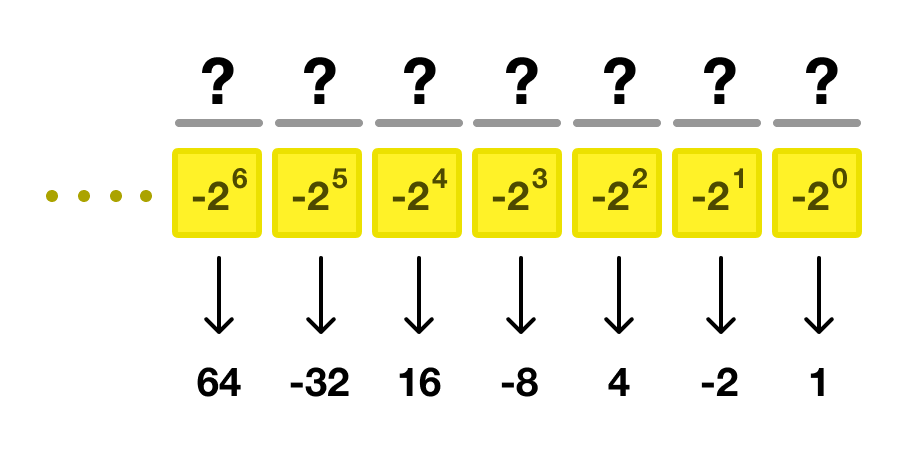
What we just did was the hardest part. Now, all that remains is to expand out the calculations and see what the final value is. This will start off as follows:

1 x (−2)⁶ + 1 x (−2)⁵ + 1 x (−2)⁴ + 1 x (−2)³ + ⏎
1 x (−2)² +1 x (−2)¹ + 0 x (−2)⁰

We can now simplify the results further and get the final answer:

64 − 32 + 16 − 8 + 4 − 2 + 0 = 42

The final result of turning the negabinary value of 1111110 into a decimal value is 42. We saw the reverse of this earlier, where we looked at how to turn 42 into negabinary, so that this all meshes up in both directions should not at all be surprising...even though it does feel like it sometimes!

Charles Simonyi’s Question

Getting back to Charles Simonyi and his negabinary-related interview question, below is an expanded snippet that talks about a few historical things about his time at Microsoft along with his negabinary-related interview question:

So yeah, I mean those days of Microsoft were incredible. We put together, we spent a lot of time hiring. I remember, for example, Bill was in the middle of everything, and we were hiring people so we were interviewing side by side at Berkeley, for example, and Princeton. And it's funny that sometimes Bill was overhearing my questions and vice versa, and at that time I was very keen on this question of base negative two. In my earlier life I saw a machine that was operating in base negative two that was a Polish serial computer. Maybe the Museum could have some record of it, but it turns out that in base negative two, there's no issue about how to represent negative numbers, so you don't have to decide as it were, you know, two's complement, one's complement, sign magnitude and all of those things that were really occupying a great deal of bandwidth during the 50s. So these guys, being mathematicians, they said well, there's one way out of it, we use base negative two, where there's no sign and negative number representation is completely well defined. But I made an exam question out of it and just said, "How do you tell, I'll give you a binary number, it's in base negative two, how do you tell whether the number is positive or negative?" And of course the answer is that you count the position of the leading bit and if it's even then it's negative, and if it's odd it's positive or the other way around, but so because the interview of positions they are worth one, minus two, four, minus eight and so on, so forth. And you know, it's something that can be solved in two or three minutes and it really distinguishes people who really can follow up on some rules in a conceptual way and those that are completely frightened by something that they haven't heard before.

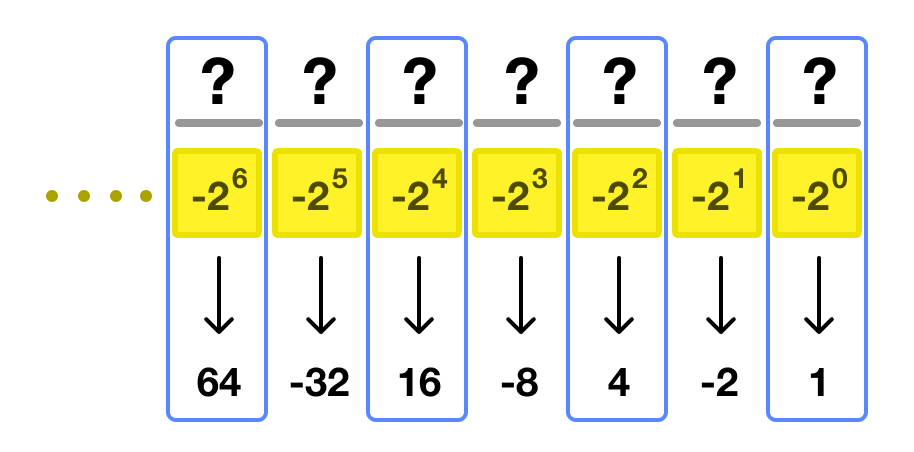
In a negabinary system (base -2), you don’t need a sign bit to tell you whether a number is positive or negative. The sign of the number is built into the pattern of the digits because the place values alternate between positive and negative powers of 2.

Remember, each digit in a negabinary number represents a power of -2:

If the position of the leading bit is on an even position (0, 2, 4, 6, etc.), the number is going to be positive:

If the position of the leading bit is on an odd position (1, 3, 5, 7, etc.) then the number is going to be negative:

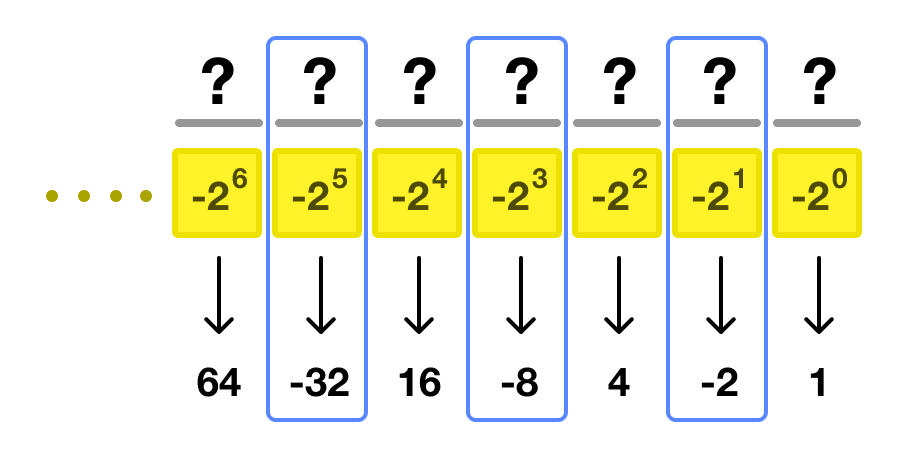
By knowing this little detail, negabinary allows us to both quickly identify whether an number is positive or negative as well as help us represent negative and positive values very elegantly. This characteristic makes negabinary a very viable choice in low-level systems programming, where you are most likely to encounter it.

Conclusion

So there you have it — negabinary, the quirky number system that flips everything (literally) on its head. What starts out sounding like a math puzzle — “let’s use negative powers of two!” — turns out to be a surprisingly elegant way to handle both positive and negative numbers without needing sign bits or complicated hacks like two’s complement. Sure, it’s not what your calculator uses, and you and I probably won’t see it pop up in your next coding interview unless you are talking to Charles Simonyi, but it’s a good mental exercise to think about how to deal with negative base values when converting between number systems.

Just a final word before we wrap up. What you've seen here is freshly baked content without added preservatives, artificial intelligence, ads, and algorithm-driven doodads. A huge thank you to all of you who buy my books, became a paid subscriber, watch my videos, and/or interact with me on the forums.

Your support keeps this site going! 😇