Have questions? Discuss this HTML5 / Canvas tutorial with others on the forums.

When drawing in the canvas, a (very superior) shape you will often want to draw is a circle:

While the circle seems like something that would be easy to draw, as you will see shortly, it has some bizarre behaviors that you need to know about. This tutorial will help you out with that and more.

Let's get started!

Meet the Arc Function

The way you draw a circle in your canvas by using the handy arc function. This function and the arguments you need to specify in order to use it look as follows:

arc(centerX, centerY, radius, startAngle, endAngle, isAntiClockwise);

These arguments are important in helping you draw the circle that you want, so let's look in detail what all of these arguments do.

centerX and centerY

The centerX and centerY arguments are pretty straightforward to understand. They specify where the center of your circle will be positioned inside the canvas:

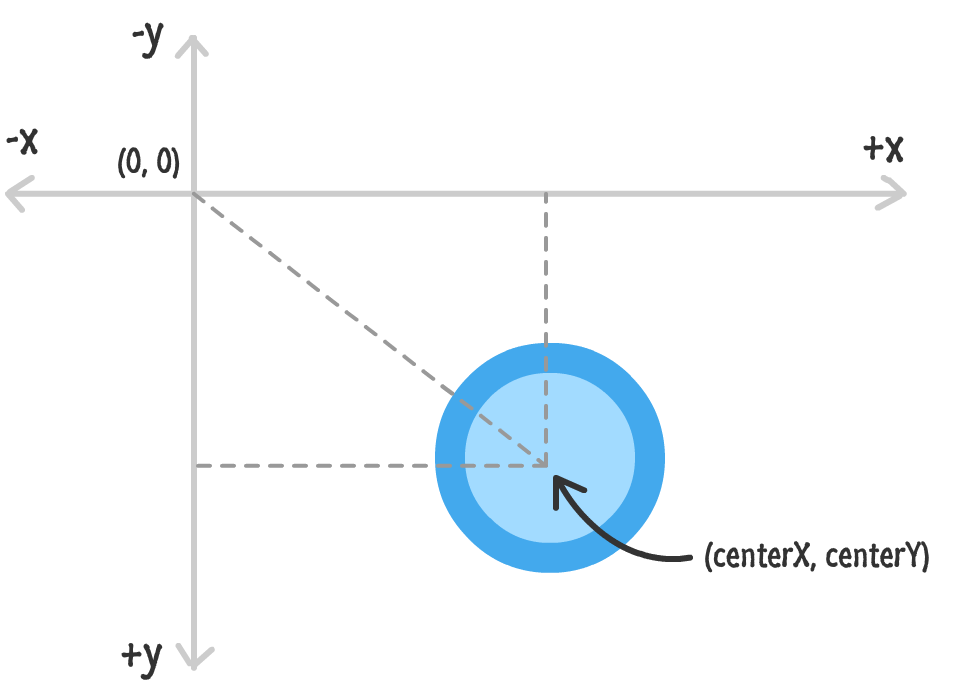
Remember, the canvas lives in an inverted Cartesian system. What this means is that the x value increases as you move right, and the y value increases as you go down. This might be a little different than what you may remember from graphing equations in school.

Radius

The radius specifies the straight line distance of your circle from its center to any edge:

 

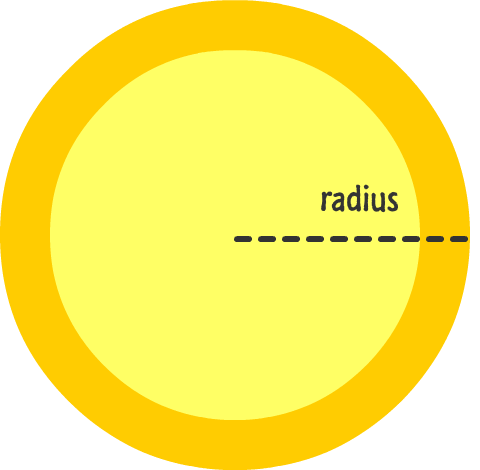
The larger your radius, the bigger your circle will be. The smaller your radius, the smaller your circle will be. If you provide a negative value, JavaScript will throw a nice IndexSizeError exception, so you don't want to do that.

startAngle, endAngle, and isAntiClockwise

Now, we finally get to the interesting stuff. These three arguments are interesting and closely related to drawing your circle. As you probably know, a circle is made up of 360 degrees:

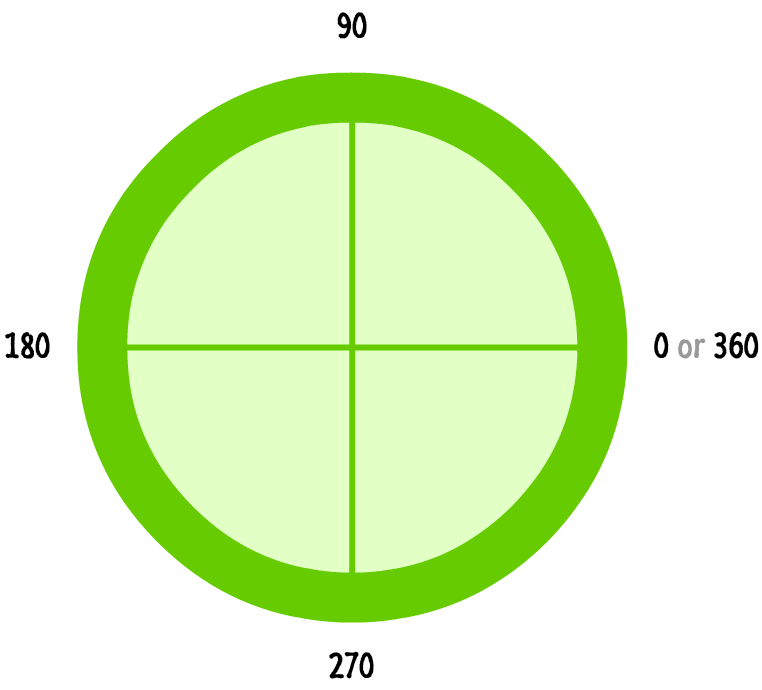
There are two important details to note - details that will probably shatter your belief in all that is good in this world. The first is that the angles increase clockwise for a circle when drawn in the canvas:

The second detail is that JavaScript doesn't work with degrees. In JavaScript land, you deal with everything in terms of radians:

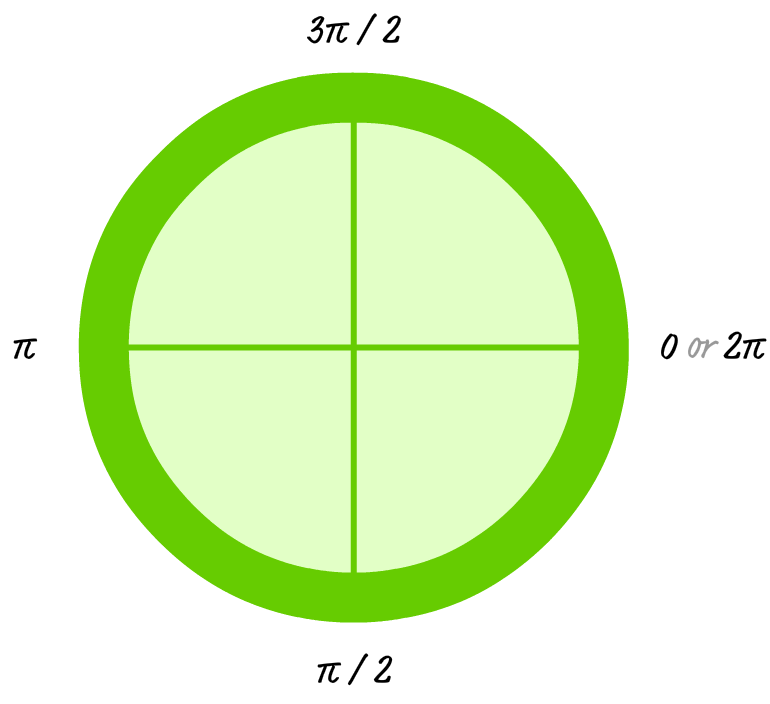
Once you understand these two details, you crossed a big hurdle in mentally being able to visualize what your arc function will create.

Ok, let's now take a step forward and work through how the startAngle, stopAngle, and isAntiClockwise arguments play a role. There are three steps you need to follow:

1. Mark your startAngle.
2. Mark your stopAngle.
3. Draw a line on the circumference either clockwise or anticlockwise depending on whether your value for isAntiClockwise is true or false.
4. If you are filling in your circle, fill in the region enclosed by the circumference and the straight line between the points referenced by startAngle and stopAngle.

Let's look through an example of this. Let's say your start angle is ᴨ / 2, and your end angle is ᴨ. You are also anticlockwise and centered at 200, 200 with a radius of 93.

Given those values, the arc function would look as follows:

arc(200, 200, 93, Math.PI / 2, Math.PI, true);

If you had to visualize this, here is what your circle with just the stroke defined would look like:

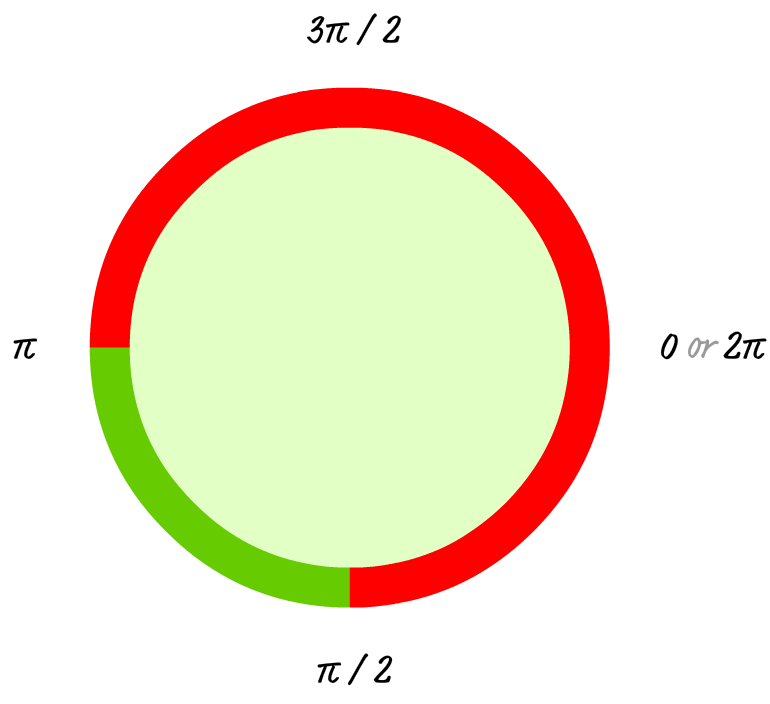
If you filled in this circle, here is what you would see:

Notice that your circle's start and end points are defined by your startAngle (ᴨ / 2) and your endAngle (ᴨ). Because you are going anti-clockwise, notice that the outline and the colored region goes all the way around the circle on the long side.

If you switch from being anticlockwise to being clockwise but keep all of your other values the same, your arc function now looks as follows:

arc(200, 200, 93, Math.PI / 2, Math.PI, false);

As a result of the direction being changed, your circle takes a different turn (ha!):

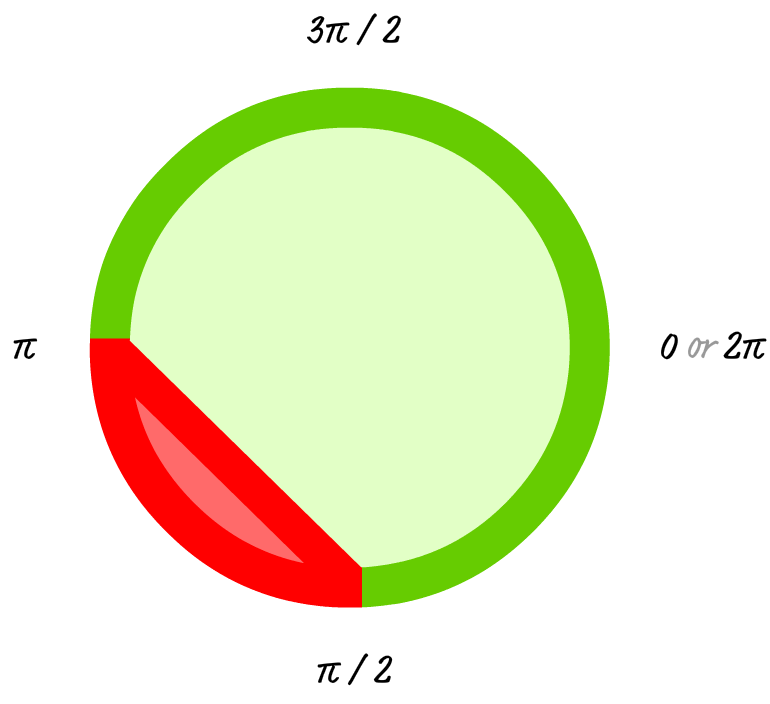
Whenever you run into the arc function and need to visualize what the final circle looks like, use the four steps I described earlier. Those steps hold for whatever combination of startAngle, endAngle, and true/false you provide for the anti-clockwiseness of your circle.

Displaying the Circle

Ok, now that you know all about the arc function and how you can mentally draw your circle, it's time to draw it for realz. Let's say that that you have some starting code that looks as follows:

var mainCanvas = document.getElementById("myCanvas");
var mainContext = mainCanvas.getContext("2d");

var canvasWidth = mainCanvas.width;
var canvasHeight = mainCanvas.height;

function draw() {

}
draw();

This code just takes care of just getting your canvas (whose id value is myCanvas) prepped for drawing content. There is nothing fancy going on here, so let's fix that. Modify your draw function by adding the following code:

function draw() {
	// draw the colored region
	mainContext.beginPath();
	mainContext.arc(200, 200, 93, Math.PI / 2, Math.PI, true);
	mainContext.fillStyle = '#FF6A6A';
	mainContext.fill();
	
	// draw the stroke
	mainContext.lineWidth = 20;
	mainContext.strokeStyle = '#FF0000';
	mainContext.stroke();
}

If you preview in your browser right now, you will see something that looks as follows:

We've already seen this weird semi-circle in the previous section, it is nice to see it being drawn from actual code as opposed to just plain English words. Before we wrap things up, let's end (ironically) by looking at the code for how to draw a full circle:

function draw() {
	// draw the colored region
	mainContext.beginPath();
	mainContext.arc(200, 200, 93, 0, 2 * Math.PI, true);
	mainContext.fillStyle = "#E2FFC6";
	mainContext.fill();

	// draw the stroke
	mainContext.lineWidth = 20;
	mainContext.strokeStyle = "#66CC01";
	mainContext.stroke();
}

When you preview this in your browser, you'll see something that looks like this:

You can tell by looking at the arguments we passed in to the arc method for why that is. The startAngle value is 0, and the endAngle value is 2ᴨ. We don't leave any room for any spoiled radians to go off and do something crazy.

Conclusion

Well, that's all there is to drawing circles on the canvas. As you've seen by now, there is no simple circle method that draws a circle for you. Instead, you have the more general arc method that provides you with a lot of little buttons to push and to customize what your circle looks like. With generality, you often get complexity. Where there is complexity, you'll probably find me writing about it. Now, isn't that the most cringe-worthy conclusion you've probably ever read? I certainly hope so :P

Just a final word before we wrap up. If you have a question and/or want to be part of a friendly, collaborative community of over 220k other developers like yourself, post on the forums for a quick response!