So you made it this far then? Ok, let's get down to some coding. I promise to make it as easy as possible so don't sweat it.

At this point, you should have a movieclip called "circle" and inside it, you'll have a circle which is 70x70 and centered on the stage. You should also have an instance of the "distancing" movieclip inside here too. Here's what mine looks like:

[ the "circle" movieclip ]

8. Ok, as I explained earlier, we're going to use the "distancing" movieclip to execute some code over and over again. This code, will be the code that calculates the distance between the mouse and this circle. The code will also then affect the circle's transparency (alpha) depending on this calculated distance so select the "distancing" clip by clicking on the white circle that represents it and open up the "Actions" panel by pressing F9 or open it from the "Window" menu.
9. Insert the following code and why not have a quick glance at it yourself to see what you can pick up before I go over it in full?
    

   onClipEvent (enterFrame) {

   xdist = Math.round(_root._xmouse - _parent._x);

   ydist = Math.round(_root._ymouse - _parent._y);

   distancefromthis = Math.round(Math.sqrt((xdist*xdist) + (ydist*ydist)));

   _parent._alpha = (100-distancefromthis)+20;

   }

   Do you recognize the formula used in fourth line? It's Pythagoras' theorem! What's that you say? Who's Pythagoras!? You should be ashamed! Never worry, here's what it is, how it works and how it applies here...

   Basically, Pythagoras' theory can be used to calculate the length of a side of a right-angled triangle given that we already know the two other sides. Here's a diagram:

   

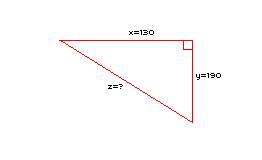
   [ it has to be a right-angled triangle ]

    

   	Pythagoras To The Rescue!
   OK, so we've got a right-angled triangle, two known sides (x and y) and an unknown hypotenuse (z). First of all, Pythagoras' theory is this:  x² + y² = z² And here's our process of working out z:   130² + 180² = z²  therefore...   16900 + 32400 = z²  therefore...   z = the squareroot of 49300 which equals 222

    

   Now let's imagine that our circle was at the top-left point of that triangle and the user's mouse was at the bottom-right point of the triangle, using that calculation and finding out "z" would give us the distance between the two! So let's figure out each of "x" and "y" individually then...

   First of all, "x" is the difference between the mouse's x value and the circle's x value. Therefore, we use the line:
    

   xdist = Math.round(_root._xmouse - _parent._x);

   Now for the "y" value. I think you can guess that it's the difference between the mouse's y value and the circle's y value. Therefore, we use the Actionscript:
    

   ydist = Math.round(_root._ymouse - _parent._y);

    

   	Note
   You should note that I have used the _parent keyword in these lines. _parent basically makes your code refer to the current object's "parent" or whichever movieclip the current object is stored within. In this case, the code is on the "distancing" movieclip and this is placed inside the "circle" movieclip (it's parent). Therefore, _parent in this case refers to the "circle" movieclip.

   We now have the distance of the x co-ordinates in the "xdist" variable and the distance between the y co-ordinates in the "ydist" variable. Let's throw these details into Pythagoras' theory in the third line of our code. The distance between the mouse and the circle (or "z") will be stored in a variable called "distancefromthis". It will contain the square root of the "xdist" variable squared plus the "ydist" variable squared. In Actionscript, this looks like this:
    

   distancefromthis = Math.round(Math.sqrt((xdist*xdist) + (ydist*ydist)));

   Notice that I have used the Math.round() function. This just rounds our result up or down to make everything a little tidier.

   
   Phew! I hope you're still with me--that was a lot to take in so pat yourself on the back. The final line of code which actually uses all our hard-earned data and affects the circle with it:
    

   _parent._alpha = (100-distancefromthis)+20;

   Again, the use of the keyword _parent means that we're affecting the circle. Then, we point to the alpha property and set it to full (100) and then subtract the "distancefromthis" variable that we figured out and, as an option, I have added 20. This 20 number is something you should play about with to make things look how you want them. You can even try messing around with the entirety of this line!

10. Now all that's left to do is to go back to your movie's root by clicking the "Scene 1" button at the top:

    

    [ clicking this from anywhere will bring you to the root ]

    And drag a bunch of the "circle" movieclips onto the stage. Test your movie and hey-presto! You should have the desired effect!