Different Approach Towards Isometric Positioning
         by senocular

Flash, being as special as it is, allows us to take a completely different approach to handling isometric positioning without the need of any kind of complicated calculation as previously mentioned. This is achieved through movie clip transformations. Because movie clips are self-contained and operate through their own timeline and own coordinate space, you have the ability to change and alter the appearance of a movie clip. on the screen and not effect any of the movie clips internal proportions. Visually, on the screen they appear altered, but this is only because, as a viewer, you are seeing them as through a transformed instance.

Lets say for example, if you were to take a movie clip, and reduce its height by 50%, the contents of that movie clip would visually shorten from the main timeline. Though, from within that movie clip, one would not see/display any signs of change. This is because the contents themselves were not altered, but rather the clip they are in.

If you haven't already caught on, the point I'm getting at is that, instead of using mathematic calculations to position objects isometrically, we can let Flash do it for us using movie clips to automatically add the needed transformations, then globalize the new point to the main timeline and position objects there to the newly acquired point.

There's two calculations needed here, one being the rotation, as we are going from a square grid to a rotated diamond like grid, and then a scaling transformation to give us that perspective look and bring us closer to the 30/26.6 degrees of isometry. This is done with two movie clips - one for each transformation.

See illustration:

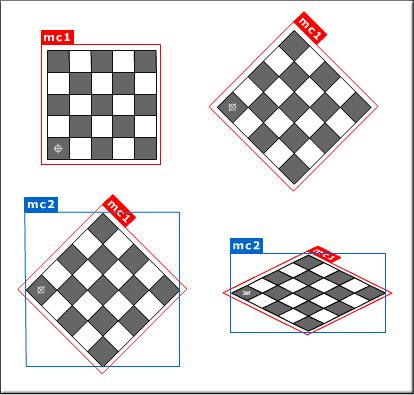
(The gray cross hairs represent (0,0)) For any movie clip. within mc1, given a normal path along say, the _x axis, that movie clip. would, on the screen, appear to traveling along the isometric angle from within those transformations. The only problem is, it too would be rotated and scaled and distorted beyond normal recognition. That is where the globalization comes into play using Flash's localToGlobal() function where you'd use either an a simple variable point or even an empty movie clip to maintain your grid position and relay that to the main timeline as a coordinate there.

For example, in a similar set up as before with the ball (_root.ball) and the grid, only the grid is transformed like described and the following code is placed on an empty clip in _root.mc1.mc2 representing the grid movement:

onClipEvent(keyDown){ if (Key.isDown(Key.UP)){ _y -= 20; }else if (Key.isDown(Key.DOWN)){ _y += 20; }else if (Key.isDown(Key.LEFT)){ _x -= 20; }else if (Key.isDown(Key.RIGHT)){ _x += 20; } point = {x: _x, y: _y}; _parent.localToGlobal(point); _root.ball._x = point.x; _root.ball._y = point.y; }
 

Transforming the point with localToGlobal() allows the ball in _root placed on that position to follow this clip precisely without any complicated calculations. All positioning within _root.mc1.mc2 (the grid) relates accordingly to the apparent isometric position when viewed from the main timeline.

Now this technique can pretty much replace that which uses the functions outlined earlier, however, the _y if you'll notice is flipped here as it is in Flash (which isn't a big deal) and this method as a whole is a little unorthodox and possibly even confusing due to its transformations. Those transformations also require going through the scope of 2 movie clips to obtain any of your desired points which in itself may be obnoxious to deal with.

Using the mathematical approach over this one is more practical and contained. It may be a little more difficult to understand but it presents itself to be the easiest to handle as everything is operated through one scope, plus it allows the methods used to be more easily ported to another language. The rest of isometric handling discussed here will be through that method.
 

Senocular