First off, before messing with isometrics, you should
know what isometry is. Isometry is equality within
measurement. What this means, is that in any isometric
representation, all measurements are to scale, no matter how
far close or how far in the distance they are in view. In an
isometric perspective, you have a 3D view where, no matter
where you are in that space, the object scaling retains its
value and doesn't change.
Conversely, in a true perspective, objects reduce in size as they recede into
the background.
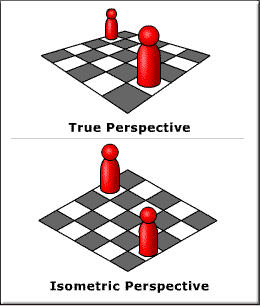
Because of this lack of perspective scaling in isometric perspectives, they
provide a way to represent a 3D object in 3D space while maintaining proportions
and hence making it reliably measurable (for the most part). The following is an
isometric cube that has all of its edges equal in length - represented in a 3D
manner without true perspective distortion.
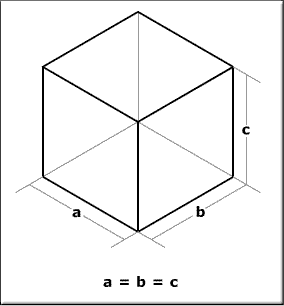
This can be invaluable in technical drawings for engineers and architects where
an object can be represented, and therefore more easily comprehended, in a
visually understandable manner but still maintains correct line measurements for
referencing. For instance, in 4-panel technical object drawings (for
engineering), much like the 4 views you see in today's 3D modeling software, you
often have a front, top, side and isometric view (though in 3D apps your
isometric is a scaled perspective).
I would whip out some of my blueprints to show this but they're buried deep
in my closet and I don't know where my digital camera is. The isometric view is
"to scale" (for the most part) and easily drawn because it relies on known
measurements. This prevents the need for the draftsperson to have to calculate
and determine perspective values for the 3D view, making it much easier and
faster to produce. The ease of creation is the true advantage to isometric
perspectives in that instance.
So far I've said "(for the most part)" twice already. What I mean by this is
that not all dimensions in isometric views are actually to scale. What are to
scale are the lines which run parallel to your x, y or z axes. Because these
lines are skewed and at unusual angles, there will be distortions in diagonals
and other lines of the such. This really isn't all that important though, and
nothing to concern yourself about.